《高频电子线路》 —— 耦合回路

文章内容来源于【中国大学MOOC 华中科技大学通信（高频）电子线路精品公开课】，此篇文章仅作为笔记分享。

---

目录

前言

耦合谐振回路

耦合回路的反射阻抗

初级等效回路

次级等效回路

次级等效回路的信号源

反射阻抗的物理意义

初级反射阻抗

电阻和反射电阻的特性

次级反射阻抗

初级和次级反射阻抗的结论

小结

耦合回路的谐振

分类

部分谐振

复谐振

全谐振

小结

---

前言

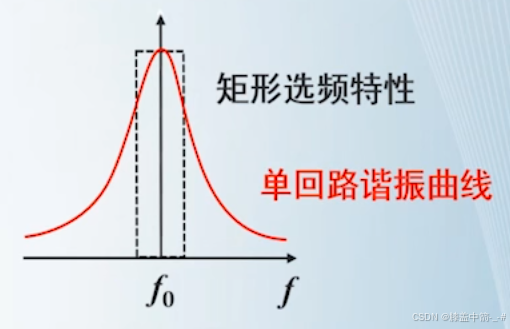对于单谐振回路而言，它的缺点是：
1、选频特性不够理想，离理想的矩形选频特性相差较远。
2、阻抗变换也不灵活、不方便。

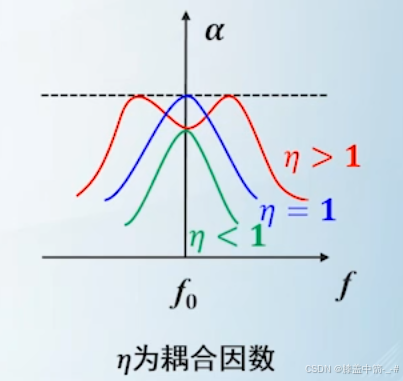红色的选频特性曲线是耦合谐振回路的选频曲线：1、它的选择性比较多。
2、离理想的矩形比单谐振回路的更要接近。

耦合谐振回路

以串联型的互感耦合的耦合回路为例进行学习。

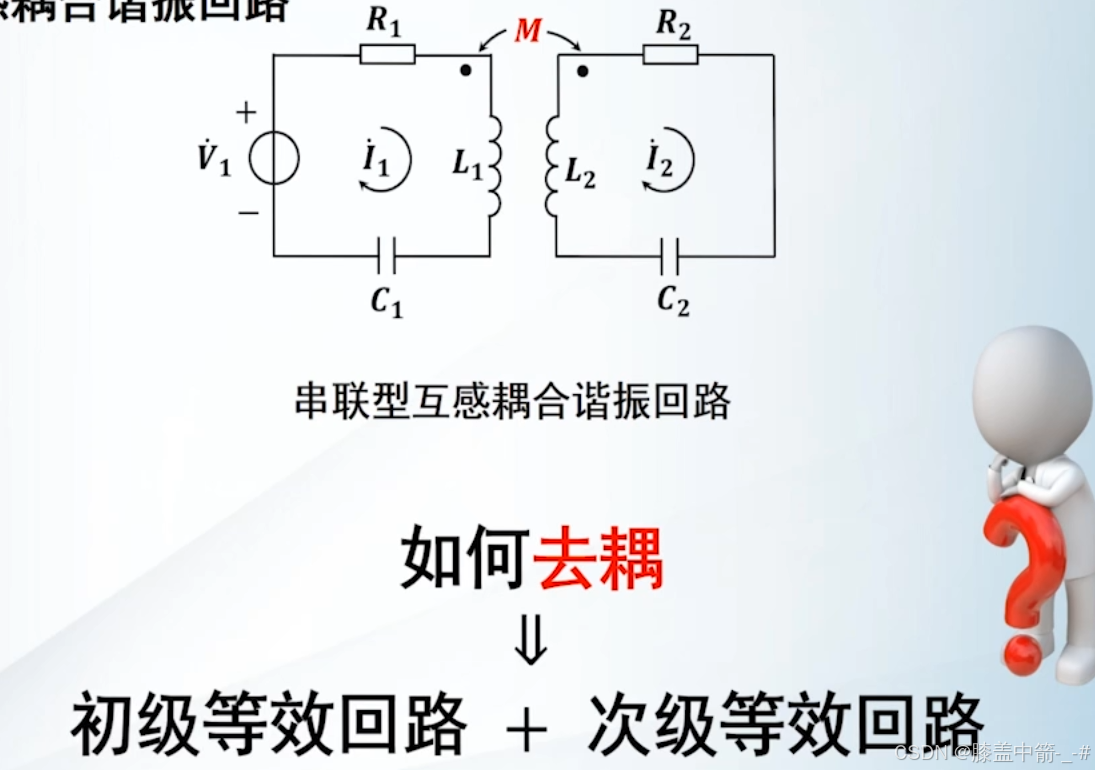
由于有互感M的存在，使得初级回路和次级回路相互影响，为了准确研究初级回路和次级回路之间的关系，需要完成去耦的工作。如何去耦呢？
可以参照此篇文章【去耦技术的简单分析】。|
去耦之后，就可以得到两个独立的初级回路和次级回路。（以下就是讲述通过反射阻抗来完成去耦的功能）

耦合回路的反射阻抗

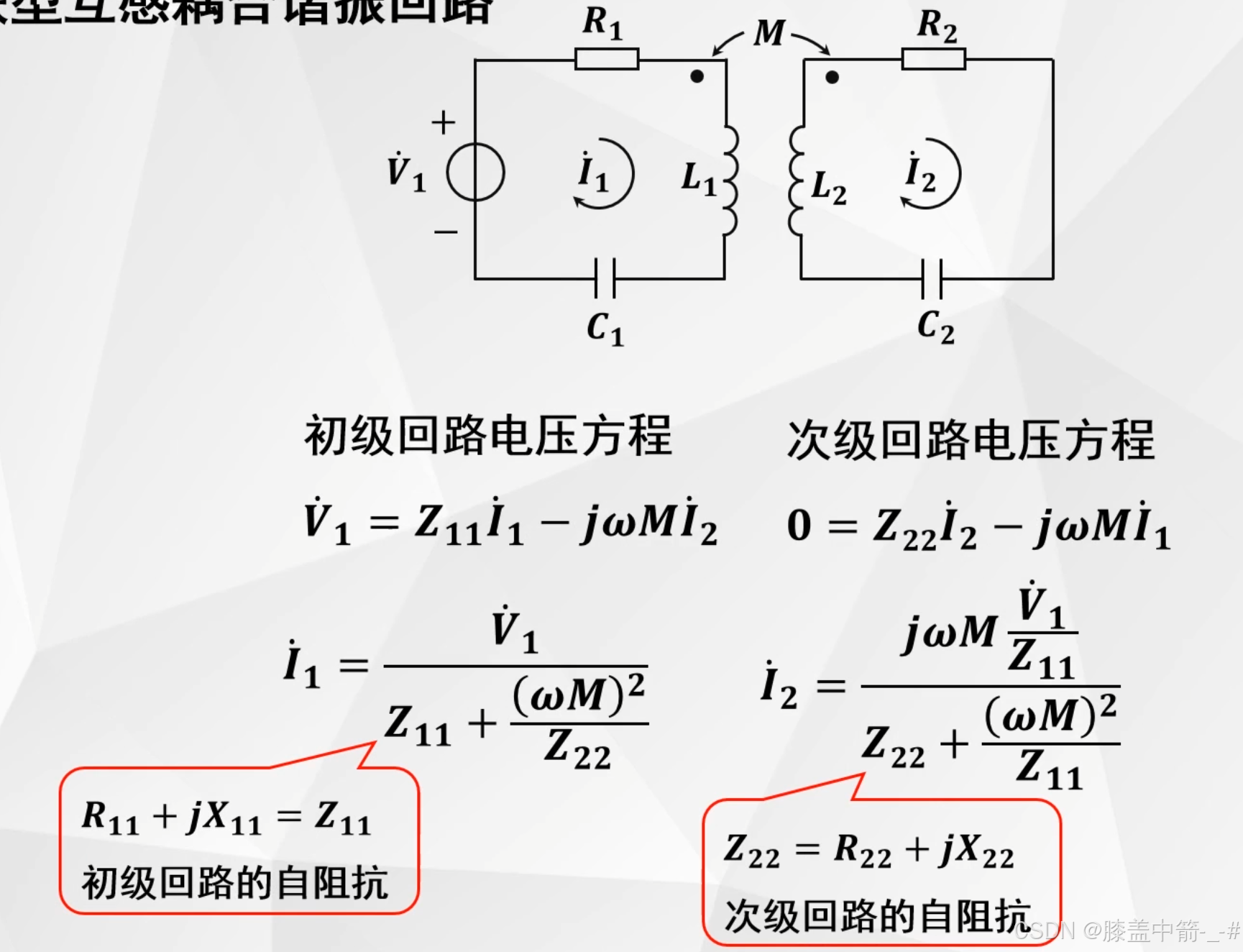
• V1代表着是初级回路的信号源。
• 第一个等式右边第二项就代表着次级回路的电流，通过互感来影响初级回路的电压。
• 次级回路没有信号源，故等号左边为0。
• 第二个等式右边第二项就代表着初级回路的电流，通过互感来影响次级回路的电压。
• 联立上面两个等式，就可以得到初级回路的电流I1和次级回路的电流I2。
• 分母部分，包括了本回路的自阻抗和另一个回路的自阻抗通过互感M反映到本回路上来的影响。

初级等效回路

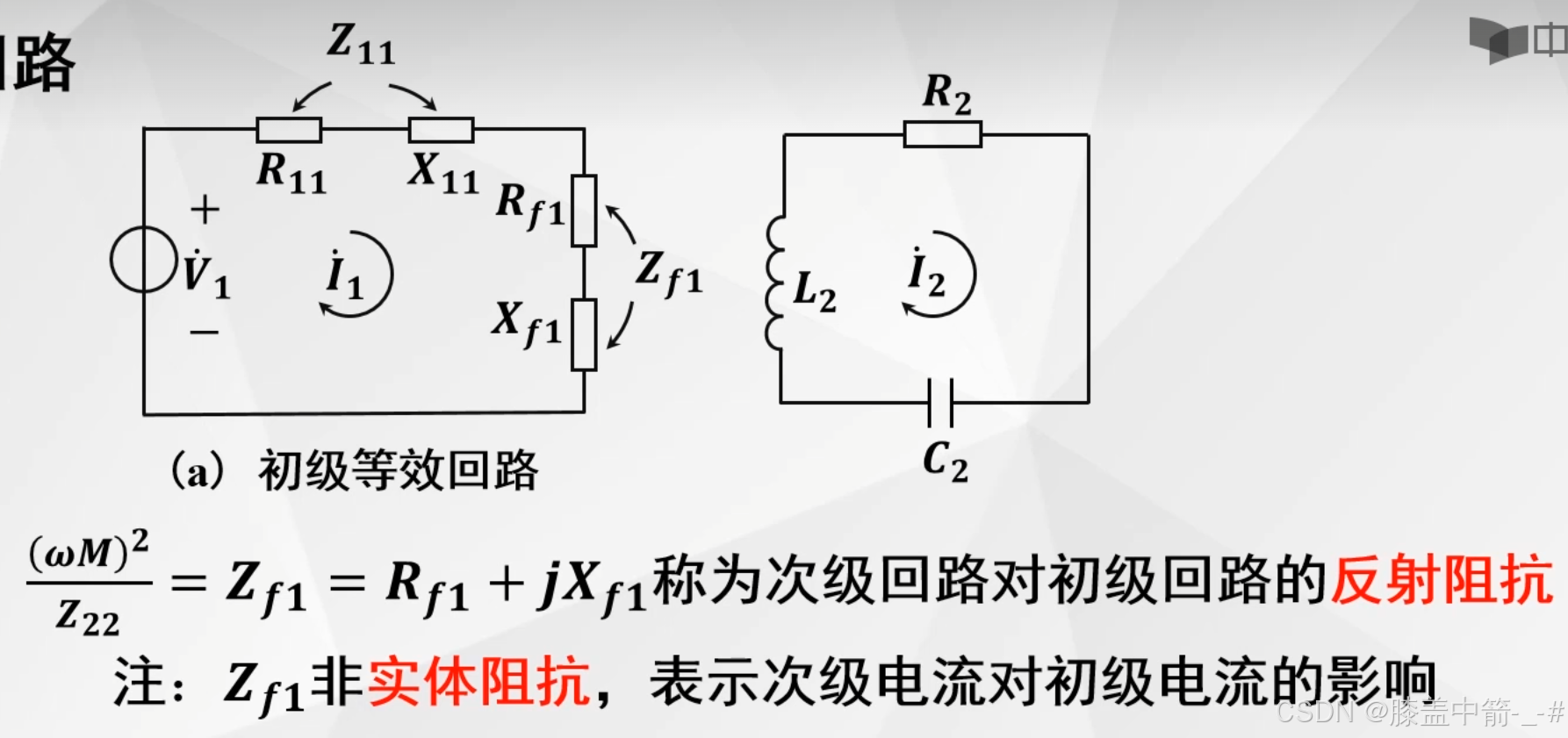
• 我们把从另一个回路通过互感M反映到本回路上来的影响也写作阻抗，叫做反射阻抗，也包括反射的电阻和反射的电抗。
• 画出来后的初级等效回路，包括初级回路的自阻抗，和反射阻抗。

次级等效回路

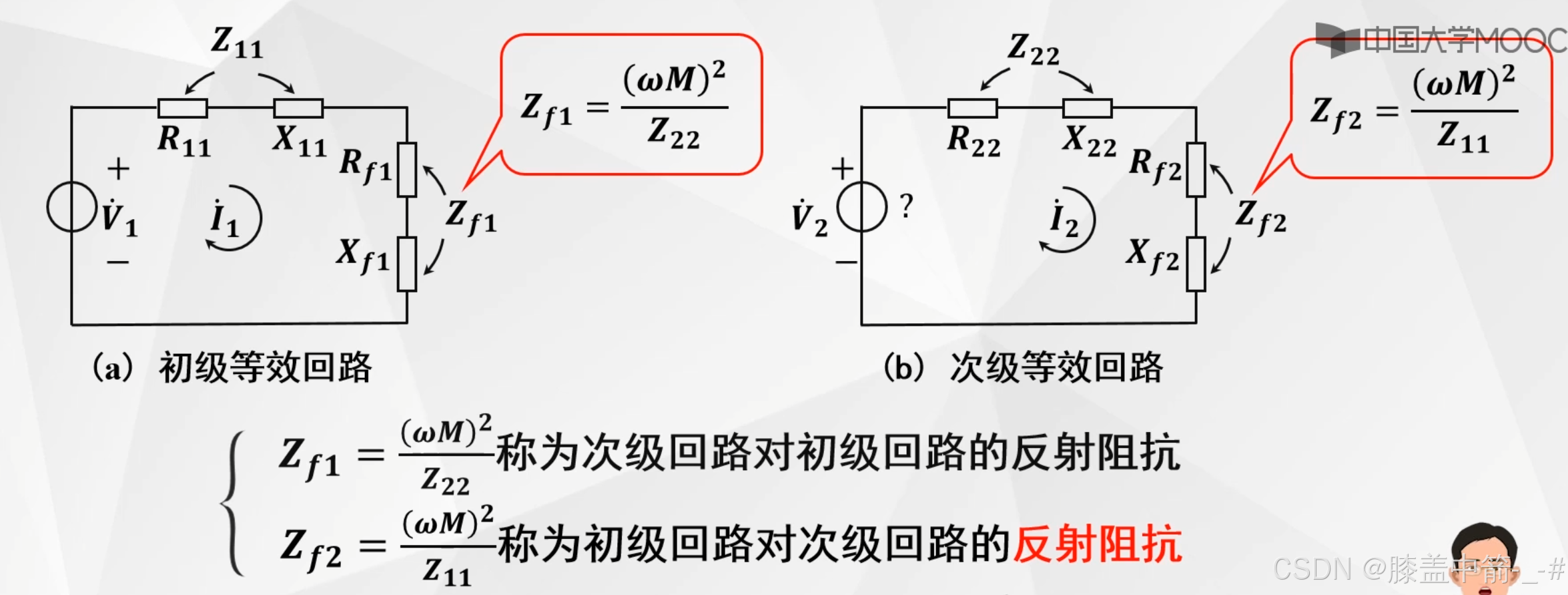
包括了自带的Z22和反射阻抗Zf2。

次级等效回路的信号源

反射阻抗的物理意义

初级反射阻抗

将初级反射阻抗分解为了电阻和电抗。

• 对于反射电阻Rf1而言，是由次级的R22反射过来，它们的符号相同，均为正。无论电阻在次级还是初级，都是正的，是因为电阻都是代表着能量的损耗。
• 对于反射电抗而言，出现了一个负号，代表着次级反射过来的电抗性质发生了改变。

为什么耦合回路中次级反射到初级电抗的性质会改变呢？本质原因是什么呢？

1、电生磁，然后再磁生电就是180的相位差，就是一个负号（待考察）。

2、

---

电阻和反射电阻的特性

• 当初级回路和次级回路同时谐振的时候，谐振意味着电抗为零。由于仅仅是原来的初级回路和原来的次级回路，不是等效回路，因此设置X11 = X22 = 0。
• 根据X22  = 0，就可以求出反射电抗Xf1为零，同时可以得到反射电阻Rf1的值。
• 由于反射电抗为零，所以反射阻抗就是纯阻，并且反射电阻Rf1与次级回路电阻R22成反比。

次级反射阻抗

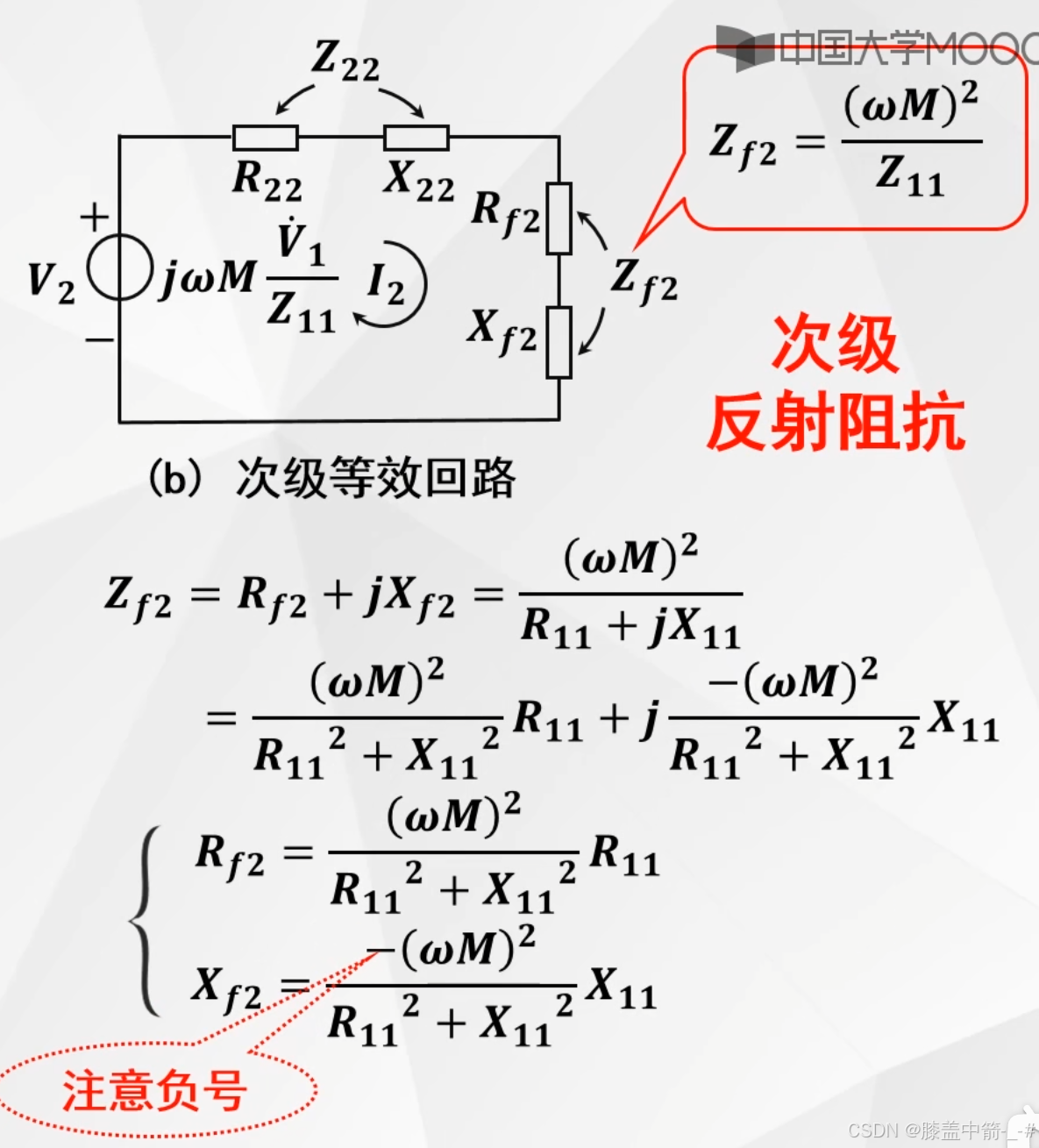
初级和次级反射阻抗的结论

小结

反射阻抗不是实体的阻抗，损耗电阻R和Rp也只会在等效电路中出现，也不存在实体的电阻。

耦合回路的谐振

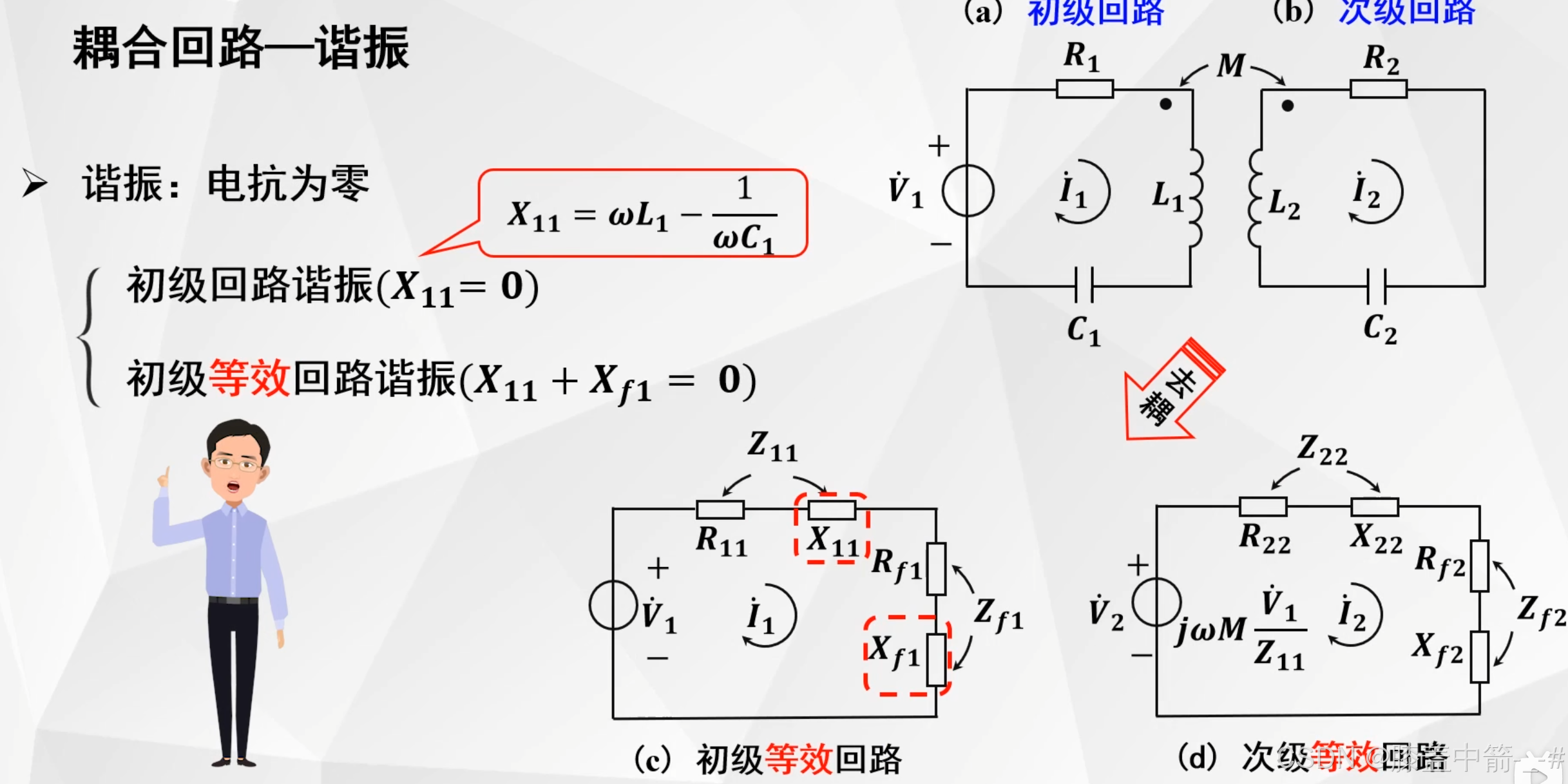
• 谐振：电抗为零
• 通过去耦后得到两个独立的等效回路，由于有两类的电路（初级、次级），所以对于谐振的定义，也分为两类。
• 初级回路谐振，意味着原来的电路中电抗为零，包括电感L1和电容C1。
• 初级等效回路谐振，那就是等效回路中所有的电抗之和为零，X11和Xf1。

---

分类

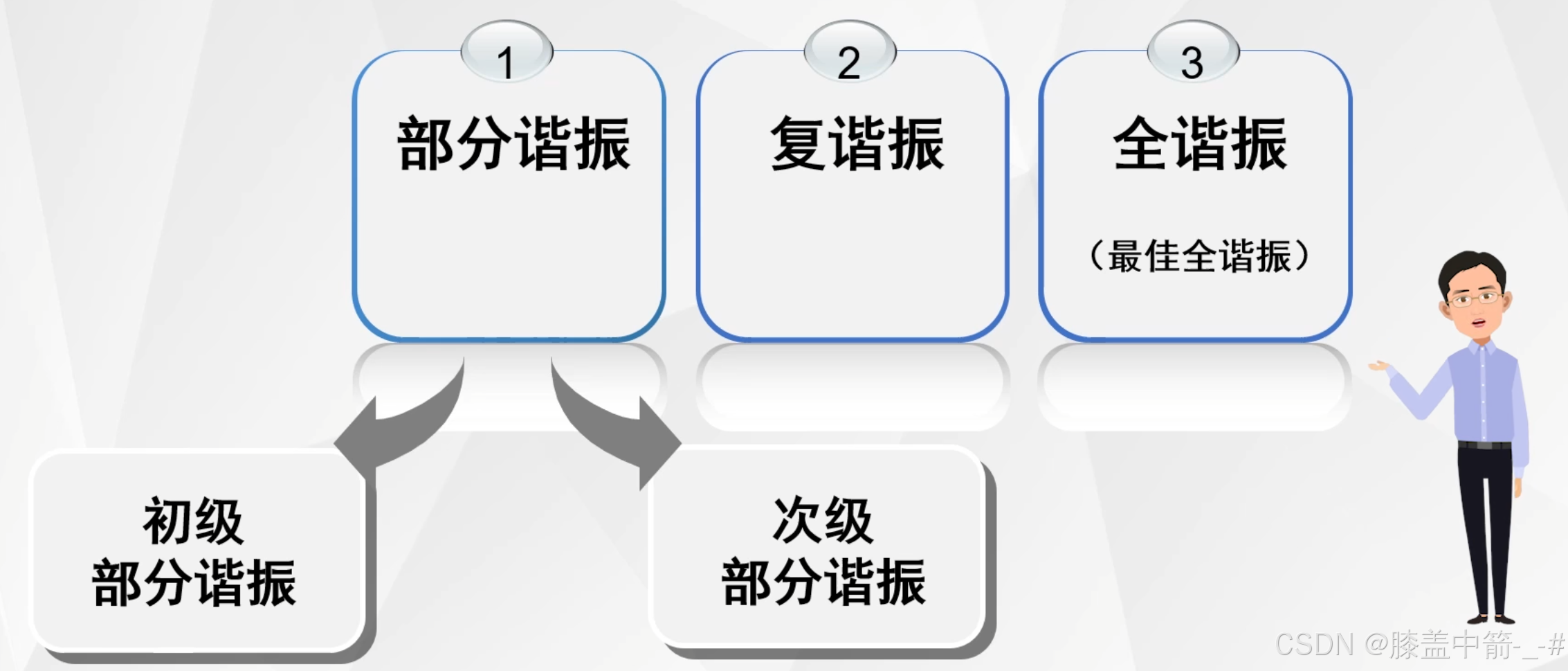
部分谐振

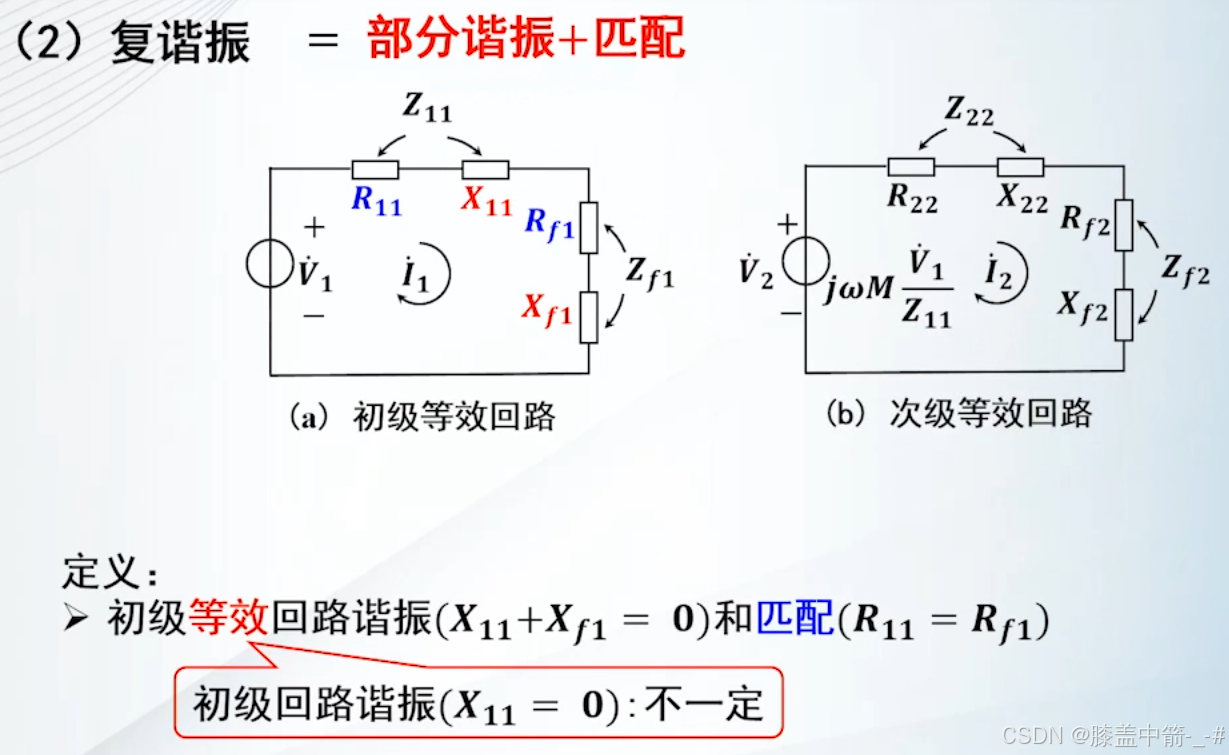
复谐振

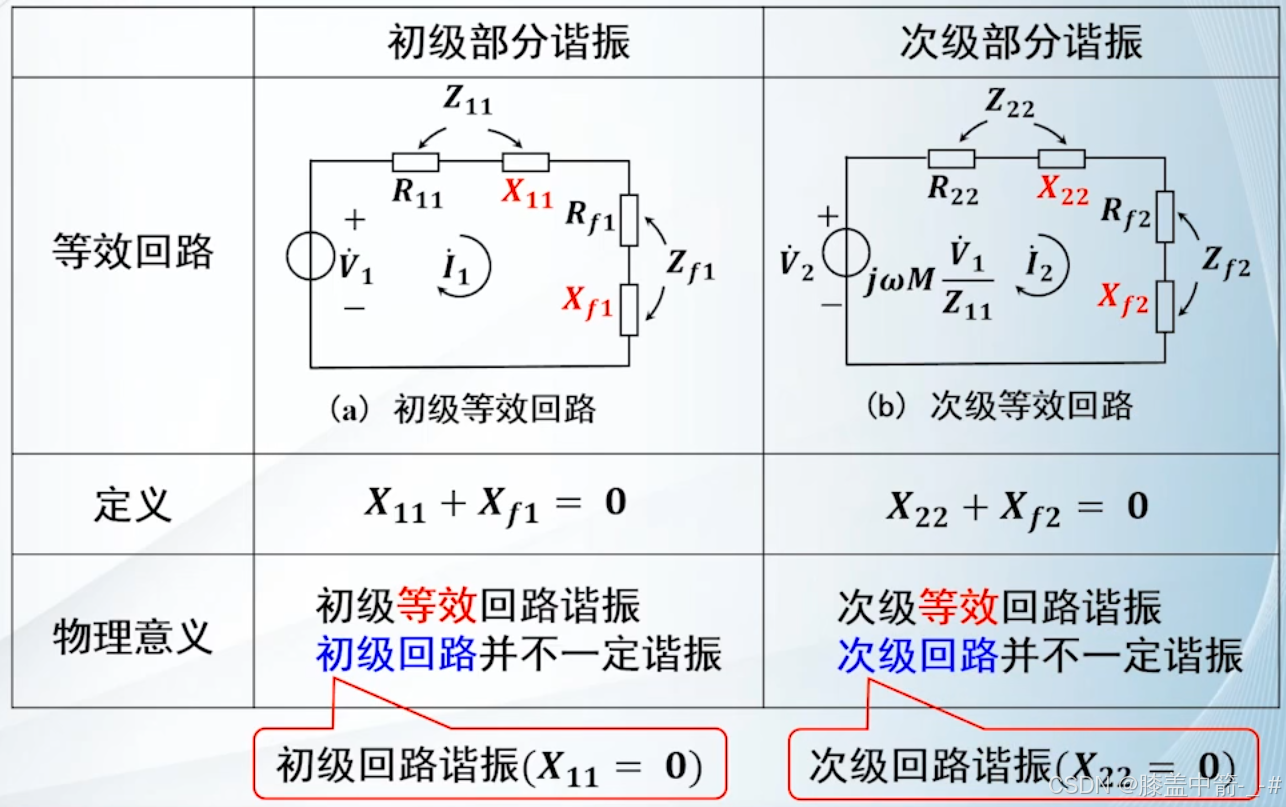
初级等效回路的谐振，并不意味着初级回路的谐振。

全谐振

耦合回路包括两个回路，只有一个回路谐振，那么就是部分谐振；如果两个回路都谐振，那么就是全谐振。

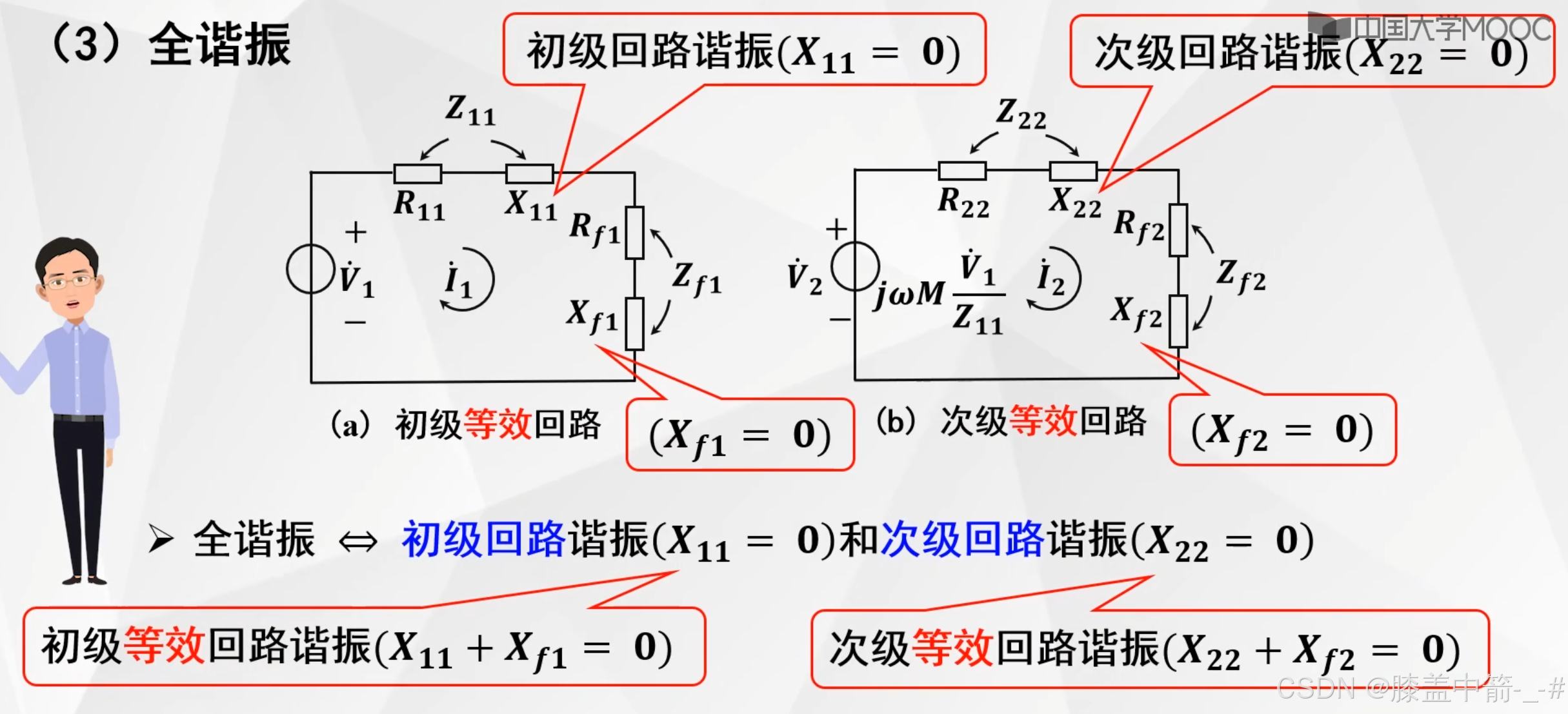
• 由于初级的自电抗X11等于零，通过反射电抗，反射到次级Xf2则也等于零。
• 次级自电抗等于零，次级等效回路的反射电抗Xf2也等于零，则可以知道次级等效回路谐振。
• 由于次级等效回路谐振，以及次级自电抗等于零，通过反射电抗到初级，初级的反射电抗Xf1等于零，加上次级回路自电抗等于零，可以得到初级等效回路也谐振。
• 总结：根据全谐振的定义可以推得，初级等效回路和次级等效回路都谐振。
  初级、次级回路谐振 -> 初级、次级等效回路谐振。

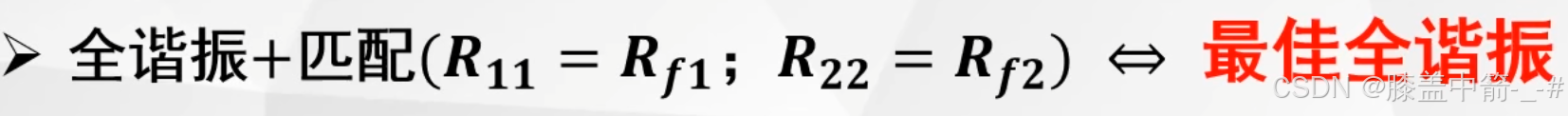
在全谐振的基础之上，初级等效回路满足匹配的条件，次级等效回路也满足匹配的条件。

小结