USACO03FALL/洛谷P2341 受欢迎的牛

题意分析

题目链接
喜欢是单向的，喜欢有传递性……Emmm这听起来好像……对了，就是连通性问题！
我们不妨将奶牛之间的喜欢关系表示为一条条单向边，怎么求明星奶牛的数量呢？
这里我们提出一个概念，缩点

设计算法

缩点是什么呢，它将环处理为点的一种方式，因为我们可以想想，如果一群奶牛呈这样的喜欢模式：

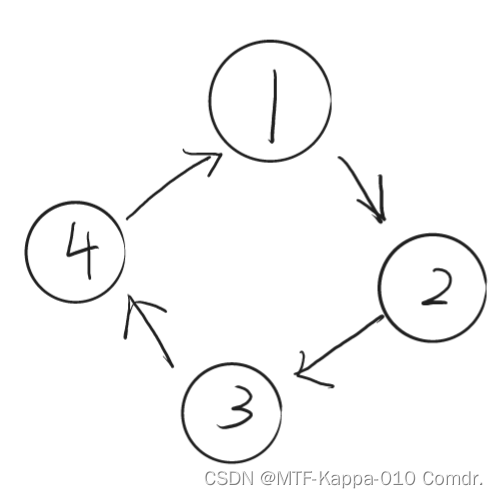
这时候不难发现其实它们可以变为一个点，因为它们之中任意一个点与其他点发生喜欢或被喜欢关系，都会在它们之中传递，呈强连通关系。因此我们只需要把它们视作一个点即可，只是如果这个“点”成为了明星奶牛，不能只按一只明星奶牛计算，而要在缩点时记录下这个”点“实际的奶牛数量

---

那么假如说我们缩完点后，如何寻找明星奶牛呢？
举个栗子
如果原来的图长这个样子：

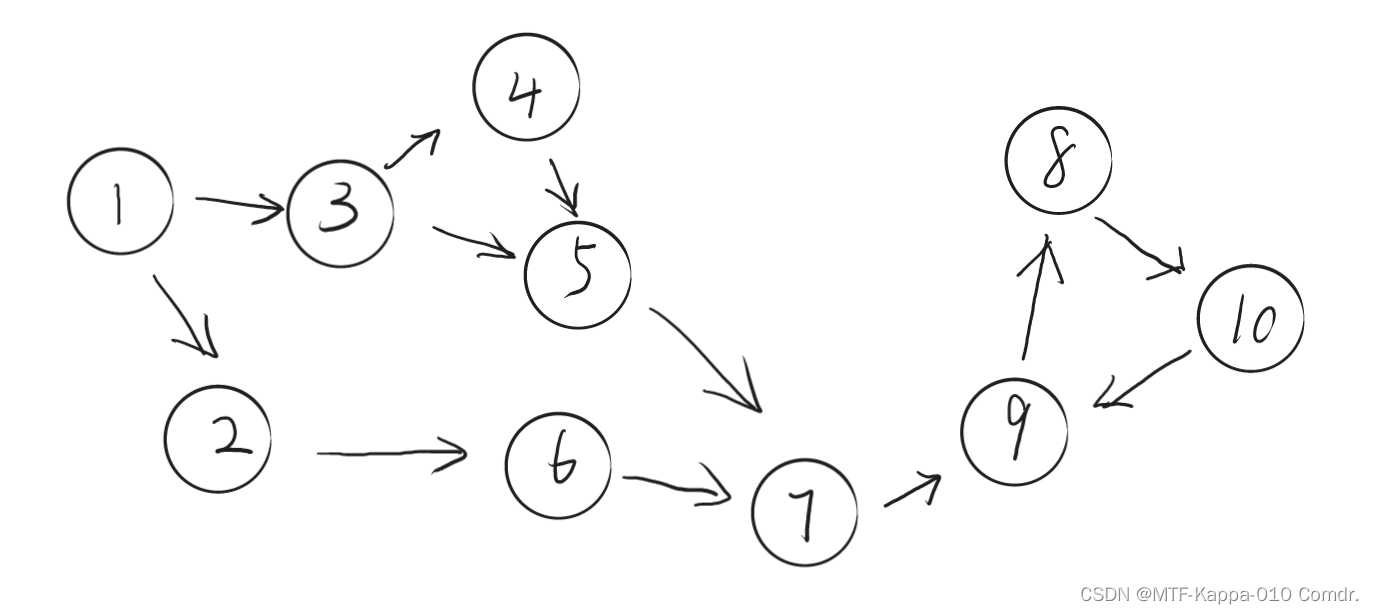
那么缩点后的图就长这个样子：

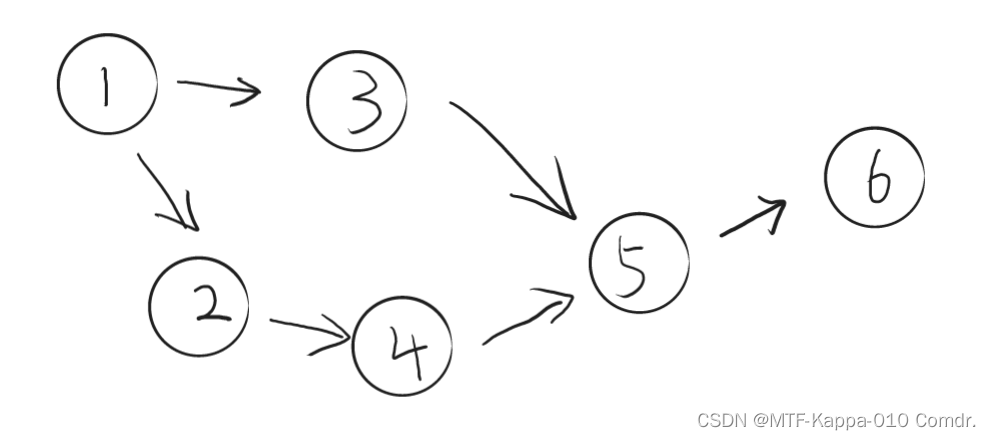
很明显明星奶牛为节点6，展开该节点发现共有3头明星奶牛
因此，重点来了！，我们可以看出此题缩点的妙处！
因为我们已经缩点了，所以图内没有任何强连通分量了，所以构成了一个层层递进，最终归于汇点的体系，那么汇点就是明星奶牛，所谓汇点，在图中，不就是出度为0的点吗！
但是，一些逻辑缜密的读者也许已经看出来了，还存在一点问题……

---

我们稍微做一点变动：

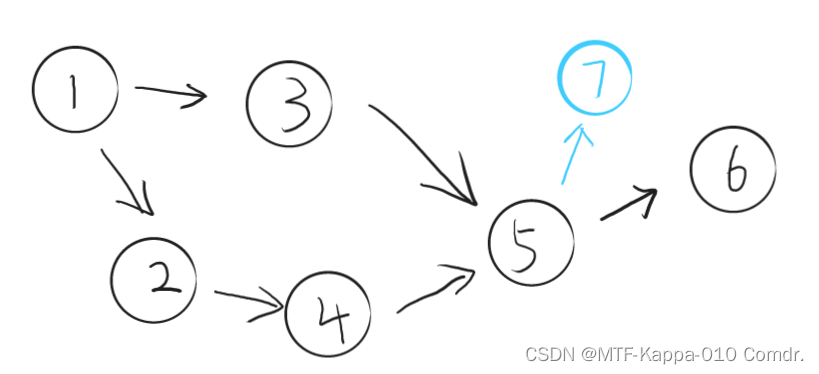
请问，在此时，还存在明星奶牛吗？显然由于加入的7谁都不喜欢，与6互不相让，最终两败俱伤，不存在任何明星奶牛
因此，我们还要对刚才做的结论进行一点修正

缩点后，若只存在一个出度为0的点，该点（或点展开后的所有奶牛）为明星奶牛，否则不存在明星奶牛

代码实现

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e4+5;
int n,m,cnt=0,scc_num/*总共强连通分量的个数*/,dfn[MAXN],low[MAXN],out_deg[MAXN]/*出度*/,fa[MAXN],scc[MAXN];
//注意scc数组存的是节点所在scc的节点个数，fa才是节点所在的scc编号
bool instack[MAXN];//是否在栈中
vector<int>g[MAXN];//我用的是链表存图
stack<int>s;
void tarjan(int x){
    dfn[x]=low[x]=++cnt;
    s.push(x);instack[x]=1;
    for(auto it:g[x]){
        if(!dfn[it]){
            tarjan(it);
            low[x]=min(low[x],low[it]);
        }
        else if(instack[x]) low[x]=min(low[x],dfn[it]);
    }
    if(low[x]==dfn[x]){//找完了一个强连通
        scc_num++;
        int cur;
        do{
            cur=s.top();s.pop();
            instack[cur]=0;
            fa[cur]=scc_num;
            scc[scc_num]++;
        }while(cur!=x);
    }
}
int main(){
    memset(scc,0,sizeof(scc));
    memset(instack,0,sizeof(instack));
    memset(out_deg,0,sizeof(out_deg));
    cin>>n>>m;
    int a,b;
    for(int i=1;i<=m;i++){
        cin>>a>>b;
        g[a].push_back(b);
    }
    for(int i=1;i<=n;i++){
        if(!dfn[i]) tarjan(i);
    }
    //求强连通分量↑
    for(int i=1;i<=n;i++){//由于我们只需要缩点后各个点的出度，所以不需要真的把图重构一遍，但是注意不是所有题都是这样
        for(auto it:g[i]){
            if(fa[i]!=fa[it]) out_deg[fa[i]]++;
        }
    }
    //缩点↑
    int scc_cnt=0,ans;
    for(int i=1;i<=scc_num;i++){
        if(out_deg[i]==0){
            scc_cnt++;
            ans+=scc[i];//缩点展开
        }
    }
    if(scc_cnt==1) cout<<ans<<endl;
    else cout<<0<<endl;//不存在明星奶牛
    return 0;
}