机器学习笔记(二、支持向量机)
本次笔记基于MOOC平台浙江大学的机器学习课程(https://www.icourse163.org/course/ZJU-1206573810)
一、线性可分问题
对于一个训练样本集{(xi,yi)},i=1~N,若存在(w,b)使得使得满足下式,则是线性可分问题。要求这样的一个超平面(在二维平面中是一条直线),则要满足以下公式
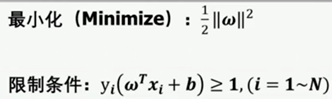
证明过程如下:
首先要确认两个事实,即

和

则可以根据线性可分问题的满足式,用a来缩放(w,b),使得找到某个非零a,存在支持向量x0上有|WTx0+b|=1,在非支持向量x0上有|WTx0+b|>1,其中,支持向量是指平面内训练集中离超平面最近距离向量。
根据上面的条件可得以下结论:
根据线性问题中要寻找的超平面的条件之一:margin最大,即d最大,所以问题就转化为求||w||最小值,为了之后的求导方面可改变为求1/2*||w||的最小值,所以要求这样一个超平面即求(w,b),则只要在限制条件下求得1/2*||w||的最小值。
因为这是一个凸优化问题,要么有唯一解要么无解,所以可以用梯度下降法求得其值。
二、线性不可分问题
对于线性不可分问题,首先要放松其限制条件,在这对每一个训练样本(xi,yi)需要设置一个松弛变量δi,所以线性可分问题里的目标函数和限制条件就变成:
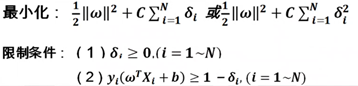
在支持向量机中解决线性不可分问题是通过将低维度映射到高纬度转化成线性可分问题解决,比如下面的例子中,用映射函数φ(x)将二维向量转化成五维向量:
这是一个二维的非线性可分问题:

我们引入φ(x)使之实现二维向量到五维向量的映射,具体的函数如下:

则不同的训练向量映射后的结果如下:
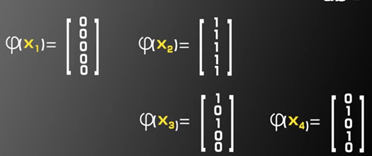
当确定(w,b)时,我们可以在高维下得到这样的不等式集,根据下面的四个不等式可知,这是线性可分的:
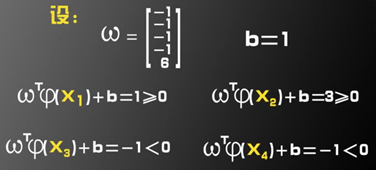
所以我们有以下结论:
假设在M维空间中随机取N个样本,并随机对每个训练样本赋予一个标签+1或-1,并假设这些训练样本线性可分的概率为P(M).
则当M区域无穷大时,P(M)=1,假设φ(x)以确定,则有如下结论:
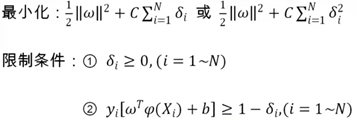
其中,这里的w也随着维度的增高而增加,这里的维度和φ(x)维度相同。
如何求解φ(x):引入核函数K(X1,X2)
许多时候很难甚至无法求得φ(x),事实上我们也不需要求解,只需要求得与其唯一对应的核函数就可以解决线性不可分问题。
核函数K(X1,X2)= φ(x1)Tφ(x2),对于这样的核函数必须满足以下式子:

对于具体的线性不可分问题的条件转化,用核函数代替φ(x)求解,涉及原问题到对偶问题的转化。
原问题的基本形式有:

其对应的对偶问题的形式则是:
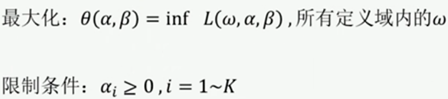
这里相关的L(w,a,ß)的定义为:
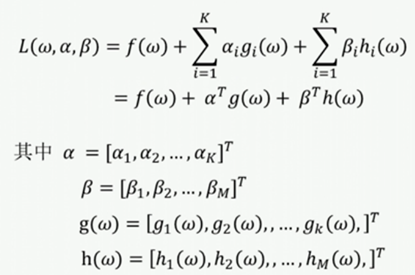
对于对偶问题目标函数的解释是遍历定义域内所有w,使函数L(w,a,ß)最小,确定这个最小值的w值,将其带入得到的相关函数则是Θ(a,ß)。
对于原问题和对偶问题有定理:假设w*是原问题的解,(a*,ß*)是对偶问题的解,则有f(w*)-Θ(a*,ß*)>0,证明不难。并且定义了对偶差距为f(w*)-Θ(a*,ß*)。
如果原问题目标函数是凸优化函数,限制条件是线性函数,则符合强对偶定理,即f(w*)=Θ(a*,ß*),不难发现,线性不可分问题符合强对偶定理。
这里有一个KTT条件:若f(w*)=Θ(a*,ß*),则i=1~K,要么ai=0,要么gi(w*)=0。
接下来是对于线性不可分问题从原问题到对偶问题的转化,观察上面的原问题的标准公式,我们先要把线性不可分的原问题转化成标准形式:
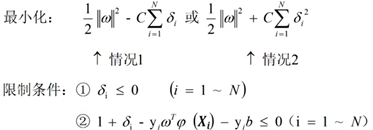
然后通过(w,b, δi)分别求偏导数,令结果为0,最后化成对偶形式:
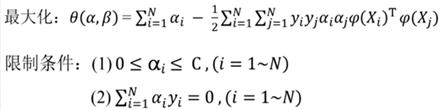
三、总结
对于前面一直到核函数的引入我都还能掌握,但是后面的原函数和对偶函数的转化我就并不能完全掌握了,只能记住结论而无法推导,同样的,对于线性不可分问题的原函数到对偶函数的转化也无法推导,只是记住了结论,虽然编程的时候不需要你深刻掌握原理。另外,我现在只是学习了理论知识,对于编程实践并不能很好的掌握和运用。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号