洛谷P1712 区间

 

题目描述

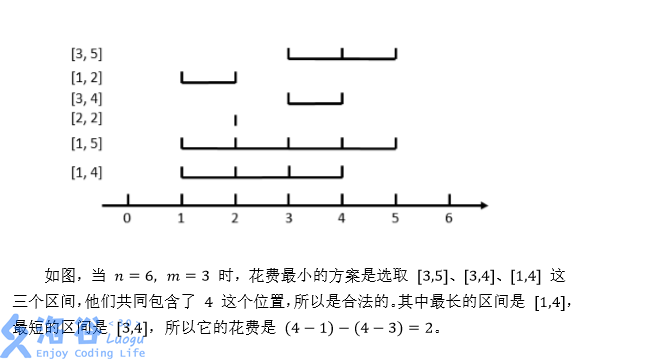
在数轴上有 n个闭区间 [l1,r1],[l2,r2],...,[ln,rn]。现在要从中选出 m 个区间，使得这 m个区间共同包含至少一个位置。换句话说，就是使得存在一个 x，使得对于每一个被选中的区间 [li,ri]，都有 li≤x≤ri。

对于一个合法的选取方案，它的花费为被选中的最长区间长度减去被选中的最短区间长度。区间 [li,ri] 的长度定义为 ri−li，即等于它的右端点的值减去左端点的值。

求所有合法方案中最小的花费。如果不存在合法的方案，输出 −1。

输入输出格式

输入格式：

 

第一行包含两个正整数 n,m用空格隔开，意义如上文所述。保证 1≤m≤n

接下来 n行，每行表示一个区间，包含用空格隔开的两个整数 li 和 ri 为该区间的左右端点。

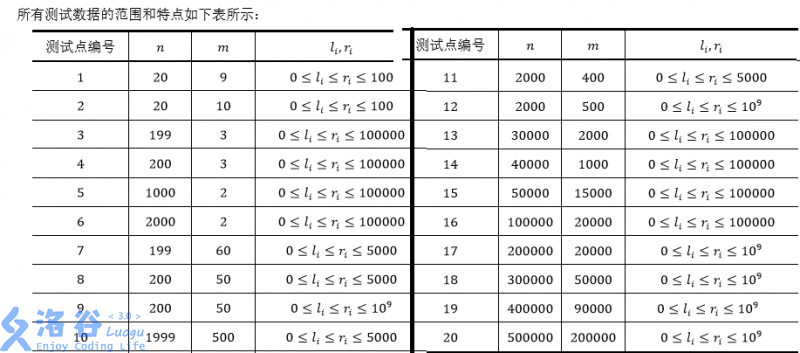
N<=500000,M<=200000,0≤li≤ri≤10^9

 

输出格式：

 

只有一行，包含一个正整数，即最小花费。

 

输入输出样例

输入样例#1：

6 3
3 5
1 2
3 4
2 2
1 5
1 4

输出样例#1：

2

说明

 

 

贪心 扫描 线段树

把区间按长度从小到大排序，依次加入。用线段树维护数轴上被覆盖的次数最多是多少，当大于m时，更新答案，并删掉最早加入的区间。

正确性显然。

 

 

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
const int mxn=500020;
int read(){
    int x=0,f=1;char ch=getchar();
    while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
struct node{
    int l,r;
    int val,mk;
}t[mxn<<3];
int rot,sz=0;
#define ls t[rt].l
#define rs t[rt].r
void pushup(int rt){
    t[rt].val=max(t[ls].val,t[rs].val);return;
}
void PD(int rt){
    if(t[rt].mk){
        if(!ls)ls=++sz;
        t[ls].val+=t[rt].mk;t[ls].mk+=t[rt].mk;
        if(!rs)rs=++sz;
        t[rs].val+=t[rt].mk;t[rs].mk+=t[rt].mk;
        t[rt].mk=0;
    }
    return;
}
void update(int L,int R,int v,int l,int r,int &rt){
    if(!rt)rt=++sz;
    if(L<=l && r<=R){
        t[rt].mk+=v; t[rt].val+=v; return;
    }
    PD(rt);
    int mid=(l+r)>>1;
    if(L<=mid)update(L,R,v,l,mid,ls);
    if(R>mid)update(L,R,v,mid+1,r,rs);
    pushup(rt);
    return;
}
struct line{
    int L,R;
    int len;
    bool operator < (const line &b)const{
        return len<b.len;
    }
}a[mxn];
int n,m,mx;
void solve(){
    int i,j;int ans=0x3f3f3f3f;
    int hd=1;
    for(int i=1;i<=n;i++){
        update(a[i].L,a[i].R,1,0,mx,rot);
        while(hd<=i && t[rot].val>=m){
//            printf("hd:%d val:%d\n",hd,t[rot].val);
            ans=min(ans,a[i].len-a[hd].len);
            update(a[hd].L,a[hd].R,-1,0,mx,rot);
            ++hd;
        }
//        printf("i:%d hd:%d\n",i,hd);
    }
    if(ans==0x3f3f3f3f)ans=-1;
    printf("%d\n",ans);
    return;
}
int st[mxn<<1],top=0;
int main(){
    int i,j;
    n=read();m=read();
    for(i=1;i<=n;i++){
        a[i].L=read();a[i].R=read();
        a[i].len=a[i].R-a[i].L+1;
        st[++top]=a[i].L;st[++top]=a[i].R;
        mx=(a[i].R>mx)?a[i].R:mx;
    }
    sort(st+1,st+top+1);
    top=unique(st+1,st+top+1)-st-1;
    for(i=1;i<=n;i++){
        a[i].L=lower_bound(st+1,st+top+1,a[i].L)-st;
        a[i].R=lower_bound(st+1,st+top+1,a[i].R)-st;
    }
    mx=top;
    sort(a+1,a+n+1);
    solve();
    return 0;
}