最优贸易问题

 

 

题目描述

C国有n个大城市和m条道路，每条道路连接这n个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这m条道路中有一部分为单向通行的道路，一部分为双向通行的道路，双向通行的道路在统计条数时也计为1条。C国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。商人阿龙来到C国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。

设C国n个城市的标号从1~n，阿龙决定从1号城市出发，并最终在n号城市结束自己的旅行。在旅游的过程中，任何城市可以重复经过多次，但不要求经过所有n个城市。阿龙通过这样的贸易方式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品——水晶球，并在之后经过的另一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来C国旅游，他决定这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。

假设C国有5个大城市，城市的编号和道路连接情况如图，单向箭头表示这条道路为单向通行，双向箭头表示这条道路为双向通行。

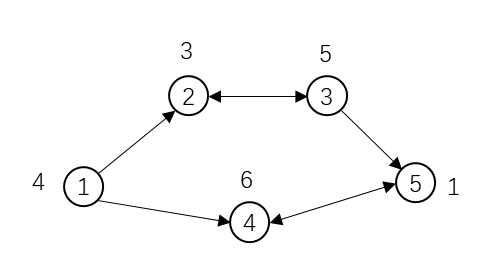
假设1~5号城市的水晶球价格分别为4，3，5，6，1。阿龙可以选择如下一条线路：1235，并在2号城市以3的价格买入水晶球，在3号城市以5的价格卖出水晶球，赚取的旅费数为2。阿龙也可以选择如下一条线路14545，并在第1次到达5号城市时以1的价格买入水晶球，在第2次到达4号城市时以6的价格卖出水晶球，赚取的旅费数为5。

现在给出n个城市的水晶球价格，m条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。

 

输入格式

第一行包含2个正整数n和m，中间用一个空格隔开，分别表示城市的数目和道路的数目。

第二行n个正整数，每两个整数之间用一个空格隔开，按标号顺序分别表示这n个城市的商品价格。

接下来m行，每行有3个正整数，x，y，z，每两个整数之间用一个空格隔开。

如果z=1，表示这条道路是城市x到城市y之间的单向道路；如果z=2，表示这条道路为城市x和城市y之间的双向道路。

 

输出格式

共1行，包含1个整数，表示最多能赚取的旅费。如果没有进行贸易，则输出0。

 

数据范围与提示

输入数据保证1号城市可以到达n号城市。

对于10%的数据，1≤n≤6。

对于30%的数据，1≤n≤100。

对于50%的数据，不存在一条旅游路线，可以从一个城市出发，再回到这个城市。

对于100%的数据，1≤n≤100000，1≤m≤500000，1≤x，y≤n，1≤z≤2，1≤各城市水晶球价格≤100。

 

输入输出样例

样例1

输入样例 复制

5 5
4 3 5 6 1
1 2 1
1 4 1
2 3 2
3 5 1
4 5 2

输出样例 复制

5

 

来源: jsoi冬令营

第一次先把问题简化，设当前节点编号为x，如果从1走不到x或者从x走不到n，那就不考虑x;

第二次将题意转化成，在所有能从1能走到并且该点能走到n点的集合中求价格的极差。

问题来了，怎么求极差？

对于每一个可行的节点x，只需要求出能够走到该点一个可行的点的价格最小值 （可行点定义为1能走到，并且该点能走到n）

比如样例中5号能走到6号，差是最大为5，并且能够再从6号走到5号，其他点这样走差不比5大，所以答案为5

那么如何求能够走到该点一个可行的点的价格最小值呢？

我们假设一个很简单的图

 

 

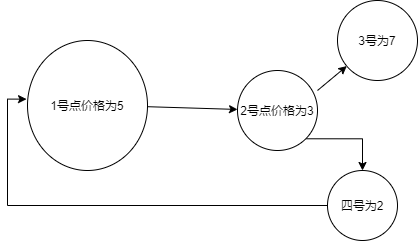
我们任取一点开始，比如从1开始，1号能直接到2号，用它的价格和2比较,2更小不更新，2更新3，3此时进价为3,2不更新4号.

4号更新了1，一号进价为2,此时继续，1号更新2，2进价为2，继续更新3，3最小进价为2,不能再更新四了，队列为空停止更新。

ans=7-2=5

可行点用正向反向两边dfs搜出公共点就可以了

//update: 有一件事，每一个点都必须入队至少一次，从一个点开始有可能会出现不能完全更新的情况，没讲请

#include <bits/stdc++.h>
using namespace std;
int n, m;
vector<int> g[100000 + 10], rg[100000 + 10];
// 正向，和反向
int w[100000 + 10], p[100000 + 10]; // w表示出售price,
//表示在能够到达该店中买价最小值
queue<int> q;
int vis[100000 + 10];
void dfs1(int id) {
  ++vis[id];
  for (int i = 0; i < g[id].size(); ++i) {
    if (vis[g[id][i]] == 0) {
      dfs1(g[id][i]);
    }
  }
}
void dfs2(int id) {
  ++vis[id];
  for (int i = 0; i < rg[id].size(); ++i) {
    if (vis[rg[id][i]] == 1) {
      dfs2(rg[id][i]);
    }
  }
}
void simply() {
  dfs1(1);
  dfs2(n);
}
int main() {
  scanf("%d%d", &n, &m);
  for (int i = 1; i <= n; ++i) {
    scanf("%d", &w[i]);
    p[i] = w[i];
    q.push(i);
  }
  for (int i = 1; i <= m; ++i) {
    int u, v, z;
    scanf("%d%d%d", &u, &v, &z);
    g[u].push_back(v);
    rg[v].push_back(u);
    if (z == 2) {
      g[v].push_back(u);
      rg[u].push_back(v);
    }
  }
  simply(); // 砍掉不需要考虑的部分
  while (!q.empty()) {
    int un = q.front();
    q.pop();
    for (int i = 0; i < g[un].size(); ++i) {
      int v = g[un][i];
      if (vis[v] == 2 && p[v] > p[un]) {
        p[v] = p[un];
        q.push(v);
      }
    }
  }
  int ans = 0;
  for (int i = 1; i <= n; ++i) {
    ans = max(ans, w[i] - p[i]);
  }
  printf("%d", ans);
} //上一次的代码是照着优先队列改回来的，所以这次纯队列我将状态去掉了一维，只考虑点的编号

 

//用优先队列 <greater> 更快，我不知道为什么