2017-10-湖南套题4

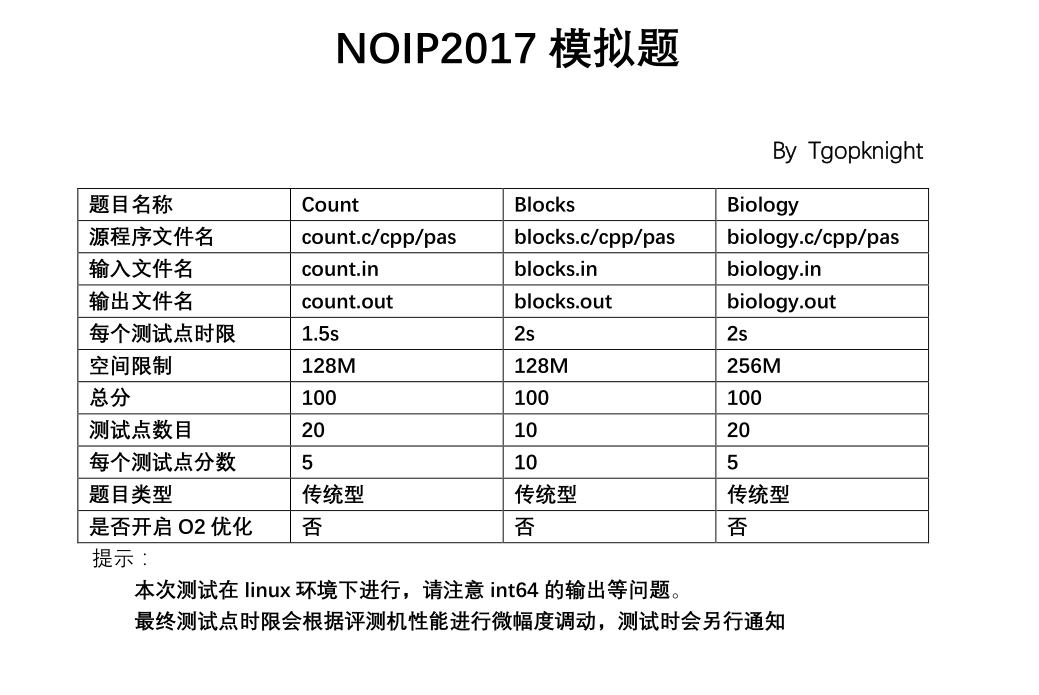
 小于等于x且与x互素的数的和=phi(x)*x/2,（一定有phi(x)对数，可以找到一个t，和与其对应的一个x-t）

所以 f[i]=i,

#include <cstdio>

#define LL long long
inline void read(int &x)
{
    x=0; register char ch=getchar();
    for(; ch>'9'||ch<'0'; ) ch=getchar();
    for(; ch>='0'&&ch<='9'; ch=getchar()) x=x*10+ch-'0';
}
const int mod(998244353);

int L,R,k,ans;

inline int Pow(int a,int b)
{
    int ret=1;
    for(; b; b>>=1, a=(1ll*(a%mod)*(a%mod))%mod )
        if(b&1) ret=(1ll*(ret%mod)*(a%mod))%mod;
    return ret;
}

int Presist()
{
    freopen("count.in","r",stdin);
    freopen("count.out","w",stdout);
    read(L),read(R),read(k);
    for(int i=L; i<=R; ++i)
//        printf("%d : %d\n",i,Pow(i,k));
    ans=(ans%mod+Pow(i,k)%mod)%mod;
    printf("%d\n",ans);
    return 0;
}

int Aptal=Presist();
int main(int argc,char**argv){;}

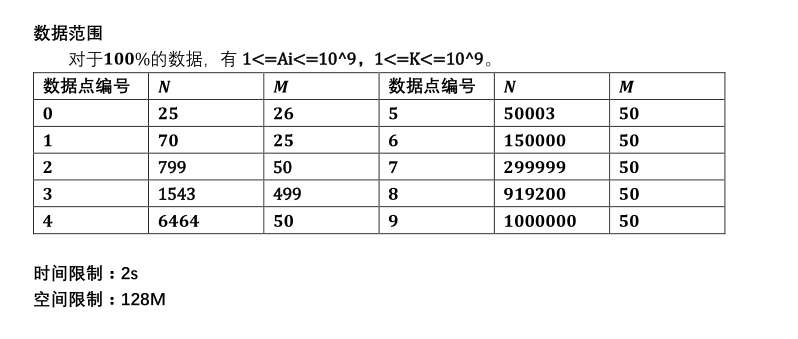
#include <cstdio>

const int Mod=998244353;
const int MAXK=1000000;

int L,R,k;
int f[MAXK+10];
int jc[MAXK+10],K[MAXK+10];
int pre[MAXK+10],suf[MAXK+10];

int power(int x,int k)
{
    int ret=1;
    while (k)
    {
        if (k&1) ret=1LL*ret*x%Mod;
        x=1LL*x*x%Mod;
        k>>=1;
    }
    return ret;
}
int cnt(int n)
{
    if (n==0) return 0;
    int ans=0;
    if (n<=k+10 || n<=MAXK)
        for (int i=1; i<=n; i++) ans=(K[i]+ans)%Mod;
    else
    {
        pre[0]=1;
        for (int i=1; i<=k+2; i++) pre[i]=1LL*pre[i-1]*(n-i)%Mod;
        suf[k+3]=1;
        for (int i=k+2; i>=1; i--) suf[i]=1LL*suf[i+1]*(n-i)%Mod;
        int l=k+1,r=0,flag=((k+1)&1)?(-1):(1);
        for (int i=1; i<=k+2; i++)
        {
            int s=1LL*pre[i-1]*suf[i+1]%Mod,m=1LL*(flag*jc[l]+Mod)*jc[r]%Mod;
            ans=(1LL*f[i]*s%Mod*power(m,Mod-2)%Mod+ans)%Mod;
            l--;
            r++;
            flag*=-1;
        }
    }
    ans=((ans+K[2])%Mod-1+Mod)%Mod;
    return ans;
}
void init()
{
    scanf("%d%d%d",&L,&R,&k);
    for (int i=1; i<=MAXK+5; i++) K[i]=power(i,k);
    jc[0]=1;
    for (int i=1; i<=k+2; i++) jc[i]=1LL*jc[i-1]*i%Mod;
    for (int i=1; i<=k+2; i++) f[i]=(f[i-1]+K[i])%Mod;
    printf("%d\n",(cnt(R)-cnt(L-1)+Mod)%Mod);
    return ;
}
int main()
{
    freopen("count.in","r",stdin);
    freopen("count.out","w",stdout);
    init();
    fclose(stdin);
    fclose(stdout);
    return 0;
}

 

 

 

 

 

因为操作次数不限，所以一段区间的平均值>=k即为一组合法解，转化为，计算a[i]-k的前缀和sum[i],区间和>=0即为合法解

设f[i]=min（j）(1<=j<=i,sum[i]-sum[j-1]>=0)，显然的若存在一个k满足k<j,且sum[k]<sum[j]，则j为无用决策、

用单调栈维护决策即可，sum具有单调性，两个指针解决

#include <cstdio>

#define max(a,b) ((a)>(b)?(a):(b))

inline void read(int &x)
{
    x=0; register char ch=getchar();
    for(; ch>'9'||ch<'0'; ) ch=getchar();
    for(; ch>='0'&&ch<='9'; ch=getchar()) x=x*10+ch-'0';
}
const int N(1e6+5);
long long sum[N];
int stack[N],top;
int n,m,a[N];

inline int Query(int k)
{
    int ret=0; top=1;
    for(int i=1; i<=n; ++i)
    {
        sum[i]=sum[i-1]+a[i]-k;
        if(sum[i]<sum[stack[top]]) stack[++top]=i;
    }
    for(int i=n; i; --i)
    {
        for(; top&&sum[i]>=sum[stack[top]]; ) top--;
        ret=max(ret,i-stack[top+1]);
    }
    return ret;
}

int Presist()
{
    freopen("blocks.in","r",stdin);
    freopen("blocks.out","w",stdout);
    read(n),read(m);
    for(int i=1; i<=n; ++i) read(a[i]);
    for(int k; m--; )
        read(k),printf("%d ",Query(k));
    return 0;
}

int Aptal=Presist();
int main(int argc,char**argv){;}

 

 

 

 

要求查找后缀相同的个数，可以将原字符串反过来求前缀，处理好多个字符串，用Trie树维护即可、以每两个要查找的字符串的原开头为起点，LCA的深度即为解

#include <cstring>
#include <cstdio>

#define swap(a,b) {int c=a;a=b;b=c;}

const int N(1000000);
char s[N];
int n,m;

int len[N],tr[N][27],tot;
int dep[N],dad[N][23];
inline void Ins(int u)
{
    int v=tot;
    dad[v][0]=u; dep[v]=dep[u]+1;
    for(int i=1; i<=20; ++i)
        dad[v][i]=dad[dad[v][i-1]][i-1];
}
inline void Build(int k)
{
    int l=strlen(s+1),now=0;
    for(int x,i=l; i; --i)
    {
        x=s[i]-'a';
        if(!tr[now][x]) tr[now][x]=++tot,
        Ins(now);   now=tr[now][x];
    }
    len[k]=now;
}

inline int LCA(int x,int y)
{
    if(dep[x]>dep[y]) swap(x,y);
    for(int i=20; i>=0; --i)
        if(dep[dad[y][i]]>=dep[x]) y=dad[y][i];
    if(x==y) return x;
    for(int i=20; i>=0; --i)
        if(dad[x][i]!=dad[y][i]) x=dad[x][i],y=dad[y][i];
    return dad[x][0];
}
/*
5 5
zzj
pri
prime
ime
owaski
2 3 1 3 5
2 2 2 3
1 actri
2 2 3 4
2 3 2 6 5
*/
int Presist()
{
    freopen("biology.in","r",stdin);
    freopen("biology.out","w",stdout);
    scanf("%d%d",&n,&m);
    for(int i=1; i<=n; ++i)    
        scanf("%s",s+1),Build(i);
    for(int op,t,u,v; m--; )
    {
        scanf("%d",&op);
        if(op==1)
            scanf("%s",s+1),Build(++n);
        else
        {
            scanf("%d%d",&t,&u);
            int lca=len[u];
            for(int i=2; i<=t; ++i)
            {
                scanf("%d",&v);
                lca=LCA(lca,len[v]);
            }
            printf("%d\n",dep[lca]);
        }
    }
//    for(int i=1; i<=tot; ++i) printf("%d ",dep[i]);
    return 0;
}

int Aptal=Presist();
int main(int argc,char**argv){;}