[Noip2018]保卫王国
这题写得心累(ˇωˇ」∠)_
题面大家都有吧
题意
~~完了我现在在难受到什么都不想写...┐(‘~`;)┌ ~~
有棵树,可以花\(p_i\)代价把\(i\)点染色,要求任2个相邻点至少有1个被染色。给出\(m\)组询问,每次强制两个点的状态(染/不染),求出每次的最小花费。
咕咕咕
\(noip2018 day2T3\) 毒瘤题,考ddp个人觉得跟天天爱跑步有得比。(代码似乎更长)
这里不讲\(O(nm)\)的暴力\(dp\)做法(大家都会吧...)
分析
很容易发现,暴力不优秀的地方在于每次都把以前算过的丢掉并重新\(O(n)\)算了一遍。我们考虑优化这一点。
假设没有任何限制,我们可以简单地先对树进行一遍\(dp\),即用\(dp[0/1][u]\)表示点\(u\)不选/选。设\(v\)为\(u\)的一个儿子,就得到一个十分重要的方程:$$\left{ \begin{array}{lr} dp[0][u]=\sum dp[1][v],\ dp[1][u]=\sum min\lbrace dp[0][v],dp[1][v]\rbrace. \end{array} \right. $$
对于一组询问\((u,v)\),由于强制选或不选,我们会把不能出现的情况的\(dp\)值置为无限大.(比如强制\(u\)选,那么我们使\(dp[0][u]=INF\)就可以),此时我们观察这对所有\(dp\)值的影响,如图(以1为根)。
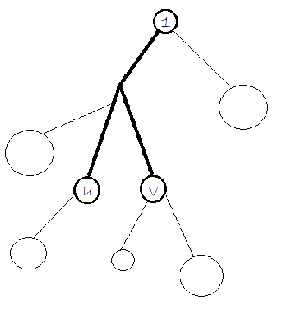
可以发现,改变的是\(u,v\)两点到根的两条链,也可看作它们到\(lca\),再从\(lca\)到根的路径。也就是说,其他的子树都可以用预先处理出来的答案直接代入!
现在问题变成了如何求这几条链上的答案。
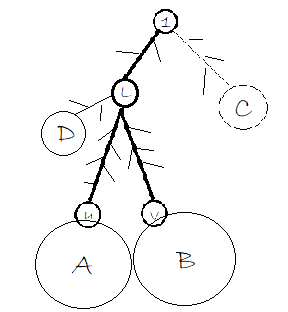
这里设\(L\)为\(u,v\)的\(lca\).那些毛一样的东西连着小的子树.
其中\(A,B\)为\(u,v\)所属子树,\(C\)是根节点\(1\)在另一边的子树,\(D\)是\(L\)的不包含\(u,v\)的子树。
于是我们现在知道\(A,B\)的答案,试图通过加粗的几条链把答案更新到根节点。因为改变\(u,v\)状态只是把一些\(dp\)值改为\(INF\),我们可以考虑也预处理出来。
倍增预处理
我们希望预处理一个\(f\)数组使\(dp\)值能快速转移。鉴于我们之前已经对树\(dp\)过,在\(f\)的状态里就不需要有关\(dp\)值的东西了(若有需要可以直接拉过来用)。我们只关心点选不选。
比如用\(f[0/1][0/1][x][y]\)表示\(x\)不选/选,\(y\)不选/选时,\(x\)到\(y\)的链(假设\(dp\)值往一个方向更新)上能得到的最大的\(dp\)值.
什么意思?
简化一下就是说,我们把x到y的链拉出来,假设y是叶子,x是根,我们从y开始往上dp,一直到x时的答案(\(min(dp[0][x],dp[1][x])\)).
有了这个,我们就可以直接把\(u\)到\(L\)和\(v\)到\(L\)的\(f\)的值加起来讨论一下啦。然鹅空间是\(n^2\)的...于是有了倍增。
设\(f[0/1][0/1][i][u]\)表示\(u\)不选/选,\(u\)往上跳\(2^i\)步的祖先不选/选时,从\(u\)开始\(dp\)到那个祖先的答案。
转移\(f\)数组很简单,只需要讨论一下\(u\)和那个祖先的中点的状态,取\(min\)就行。并且可以证明,这样的一个方程对于确定的\(x\)和\(i\),值都是固定的。
现在你可能发现问题了...
那些毛怎么办?
显然这些子树都是计算过的,可以直接把\(dp\)值拉过来。所以我们重定义方程。
设\(f[0/1][0/1][i][u]\)表示\(u\)不选/选,\(u\)往上跳\(2^i\)步的祖先不选/选时,从\(u\)开始(不包括u)\(dp\)到 \(u\)往上跳\(2^i\)步的祖先 且计入其他子树的最终\(dp\)值。即在整个祖先的子树中减去u的子树的影响。
\(e.g.\)
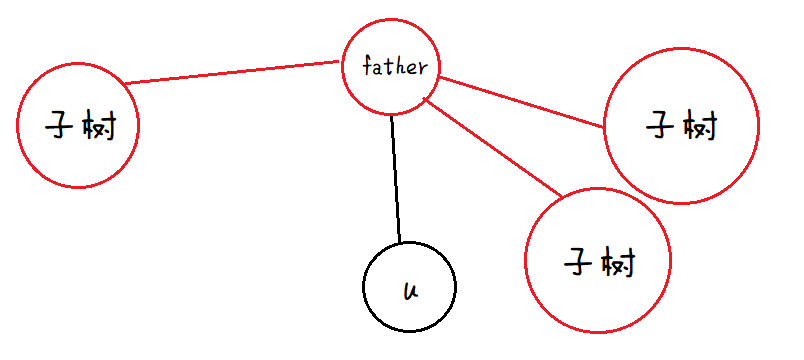
f[0/1][0/1][0][u]即为上图红色部分的贡献。
好了,这样我们可以直接把\(u,v\)到\(L\)的路径上的\(f\)数组加起来,并加上\(u\)的子树的\(dp\)值和\(v\)的子树的\(dp\)值,添上图中\(D\)的贡献,再从\(L\)开始加到根节点,以及加上图中\(C\)的贡献,就能算出总费用啦...(し)
还有一些问题
显然一开始做出的\(dp\)值都是包含当前我们在做的链下面的子树的贡献的,比如我们要用新的\(u\)的\(dp\)值更新出新的\(u\)的父亲\(fa\)的\(dp\)值时,要计算\(fa\)的别的子树的贡献,它保存在\(dp[0/1][fa]\)中,可是\(dp[0/1][u]\),即我们当前要替换的旧的\(dp\)值也算在里面了,怎么办?
显然,设新的\(u\)的\(dp\)值为\(New\),新的\(fa\)的\(dp\)值即为\(\left\{ \begin{array}{cc} &dp[0][fa]-dp[1][u]+New, \\ or &dp[1][fa]-min\lbrace dp[0][u],dp[1][u] \rbrace+New \end{array} \right.\)
\(lca\)处的新\(dp\)值怎么算?
为了方便,我们在做\(u,v\)的时候更新到\(lca\)的儿子处,并讨论\(lca\)的状态即可,具体都可见代码。
特殊情况?
当\(u,v\)在一条链上时,倍增\(u\)之后已经在\(lca\)上了,此时直接倍增\(lca\)即可;
当\(lca\)为根节点时,显然不需要倍增\(lca\),此时直接算出总答案。
总结
大致步骤如下:
1.\(dfs\)预处理\(dp\)数组和\(f\)数组(倍增数组);
对于询问:
2.将深度大的点\(u\)往\(v\)的深度跳(类似倍增\(lca\))同时更新新的\(dp\)值;
3.\(u,v\)同时往上跳至\(lca\)的儿子处同时更新新的\(dp\)值;
4.得到\(lca\)的\(dp\)值,再往上跳至根节点的儿子处同时更新新的\(dp\)值;
5.讨论根节点的状态得出最终答案。(特殊情况见上)
代码
好丑啊...⁄(⁄⁄•⁄ω⁄•⁄⁄)⁄
#include <iostream>
#include <cstdio>
#include <cctype>
#define il inline
#define vd void
#define mn 100005
#define INF 100000000000000 //1e14
#define rg register
#define ll long long
#define rep(i,x,y) for(register int i=x;i<=y;++i)
#define drp(i,x,y) for(register int i=x;i>=y;--i)
using namespace std;
const int Len=2333333,aa[18]={1,2,4,8,16,32,64,128,256,512,1024,2048,4096,8192,16384,32768,65536,131072};
char buf[Len],*p1=buf,*p2=buf,duf[Len],*q1=duf;
il char gc(); il int rd(); il vd pc(char c); il vd rt(ll x); il vd flush();
template<class T> il T Max(T a,T b){return a>b?a:b;}
template<class T> il T Min(T a,T b){return a<b?a:b;}
int n,m,ty,u,v,cnt,x,y,p[mn],h[mn],fa[19][mn],dep[mn],Log[mn];
ll dp[3][mn],f[3][3][19][mn];
struct E{int to,nxt;}e[mn<<1];
il vd Add(int u,int v){e[++cnt]=(E){v,h[u]},h[u]=cnt;}
vd Dfs(int u){
dep[u]=dep[fa[0][u]]+1,dp[1][u]=p[u],f[0][0][0][u]=INF; //相邻点不能都为0
for(rg int i=1;aa[i]<dep[u];++i) fa[i][u]=fa[i-1][fa[i-1][u]];
for(rg int i=h[u];i;i=e[i].nxt){int v=e[i].to;
if(v!=fa[0][u]) fa[0][v]=u,Dfs(v),
dp[0][u]+=dp[1][v],dp[1][u]+=Min(dp[0][v],dp[1][v]);
} //以上为dp转移
}
vd Cfs(int u){
//f[0][1][0][u]=dp[1][fa[0][u]]-dp[0][u],
//f[1][0][0][u]=dp[0][fa[0][u]]-dp[1][u],
//f[1][1][0][u]=dp[1][fa[0][u]]-dp[1][u];
f[1][0][0][u]=dp[0][fa[0][u]]-dp[1][u],
f[0][1][0][u]=f[1][1][0][u]=dp[1][fa[0][u]]-Min(dp[0][u],dp[1][u]);
for(rg int i=1;aa[i]<dep[u];++i){
int F=fa[i-1][u];
f[0][0][i][u]=Min(f[0][0][i-1][u]+f[0][0][i-1][F],f[0][1][i-1][u]+f[1][0][i-1][F]),
f[0][1][i][u]=Min(f[0][0][i-1][u]+f[0][1][i-1][F],f[0][1][i-1][u]+f[1][1][i-1][F]),
f[1][0][i][u]=Min(f[1][0][i-1][u]+f[0][0][i-1][F],f[1][1][i-1][u]+f[1][0][i-1][F]),
f[1][1][i][u]=Min(f[1][0][i-1][u]+f[0][1][i-1][F],f[1][1][i-1][u]+f[1][1][i-1][F]);
}// 4种情况的合并
for(rg int i=h[u];i;i=e[i].nxt) if(e[i].to!=fa[0][u]) Cfs(e[i].to);
}
il vd Work(){
if(dep[u]<dep[v]) swap(u,v),swap(x,y);
int L;
ll u0=INF,u1=INF,v0=INF,v1=INF,l0=INF,l1=INF,ans;
x?u1=dp[1][u]:u0=dp[0][u],y?v1=dp[1][v]:v0=dp[0][v];
for(rg int i=Log[dep[u]-dep[v]];i>=0;--i) if(dep[u]-aa[i]>=dep[v]){
ll t0=u0,t1=u1;
u0=Min(t0+f[0][0][i][u],t1+f[1][0][i][u]),
u1=Min(t0+f[0][1][i][u],t1+f[1][1][i][u]),
//printf("%d ",u);
u=fa[i][u];
//printf("%d %lld %lld\n",u,u0,u1);
} //u往上跳
if(u==v) L=u,y?l1=u1:l0=u0; //在1条链上
else{
for(rg int i=Log[dep[u]-1];i>=0;--i) if(fa[i][u]!=fa[i][v]){
ll t0=u0,t1=u1,p0=v0,p1=v1;
u0=Min(t0+f[0][0][i][u],t1+f[1][0][i][u]),
u1=Min(t0+f[0][1][i][u],t1+f[1][1][i][u]),
v0=Min(p0+f[0][0][i][v],p1+f[1][0][i][v]),
v1=Min(p0+f[0][1][i][v],p1+f[1][1][i][v]),
u=fa[i][u],v=fa[i][v];
} //一起跳
L=fa[0][u],l0=dp[0][L]-dp[1][u]-dp[1][v]+u1+v1,
l1=dp[1][L]-Min(dp[0][u],dp[1][u])-Min(dp[0][v],dp[1][v])+Min(u0,u1)+Min(v0,v1);
}// 注意这里减去两个儿子的贡献
//printf("%d\n",L);
if(L==1) ans=Min(l0,l1); //特判L=1
else{
for(rg int i=Log[dep[L]-2];i>=0;--i) if(dep[L]-aa[i]>1){
ll t0=l0,t1=l1;
l0=Min(t0+f[0][0][i][L],t1+f[1][0][i][L]),
l1=Min(t0+f[0][1][i][L],t1+f[1][1][i][L]),
L=fa[i][L];
}//L往上跳
ans=Min(dp[0][1]-dp[1][L]+l1,dp[1][1]-Min(dp[0][L],dp[1][L])+Min(l0,l1));
}
rt(ans<INF?ans:-1),pc('\n');
}
int main(){
n=rd(),m=rd(),ty=rd();
rep(i,1,n) p[i]=rd();
rep(i,2,n) u=rd(),v=rd(),Add(u,v),Add(v,u),Log[i]=Log[i>>1]+1;
Dfs(1),Cfs(1);
//rep(i,1,n) printf("%d 0:%lld 1:%lld\n",i,dp[0][i],dp[1][i]);
//puts("");
//int P=1;
//rep(i,1,n) printf("%d %lld %lld %lld %lld\n",i,f[0][1][P][i],f[1][0][P][i],f[1][1][P][i],f[0][0][P][i]);
//puts("");
while(m--) u=rd(),x=rd(),v=rd(),y=rd(),Work();
return flush(),0;
}
il char gc(){return p1==p2&&(p2=(p1=buf)+fread(buf,1,Len,stdin),p1==p2)?-1:*p1++;}
il int rd(){char c; int f=1;
while(!isdigit(c=gc())&&c!='-');
c=='-'?f=-1,c=gc():0; int x=c^48;
while(isdigit(c=gc())) x=((x+(x<<2))<<1)+(c^48);
return x*f;
}
il vd pc(char c){q1==duf+Len&&fwrite(q1=duf,1,Len,stdout),*q1++=c;}
il vd rt(ll x){x<0?pc('-'),x=-x:0,pc((x>=10?rt(x/10),x%10:x)+48);}
il vd flush(){fwrite(duf,1,q1-duf,stdout);}
有点Luosuo...还有问题大家一定要提出啊ioi


 浙公网安备 33010602011771号
浙公网安备 33010602011771号