属性基加密（ABE）基础知识

属性基加密（ABE）的分类

属性基加密（ABE）的思想来源于模糊身份基加密（FIBE），属性基加密的思想是让密文和密钥与属性集合和访问结构产生关联，当且仅当属性集合满足访问结构的时候，方能解密成功。那么根据这其中两两的对应关系，又可以将属性基加密分为两类，即密钥策略属性基加密（KP-ABE）和密文策略属性基加密（CP-ABE）。

• KP-ABE: 用户的密钥中蕴含访问结构（访问策略），密文中对应着一系列属性集合，当且仅当密文的属性集合满足用户密钥的访问结构时，用户才能解密成功。细想下来，用户是主体，只有特定的密文才能与之匹配，从而解密。

• CP-ABE: 用户的密钥对应着一系列属性的集合，密文中蕴含着访问结构（策略），当且仅当用户的属性集合满足密文的访问结构时，用户才能解密成功。细想下来，密文是主体，只有特定的密钥才能与之匹配，从而解密。
  

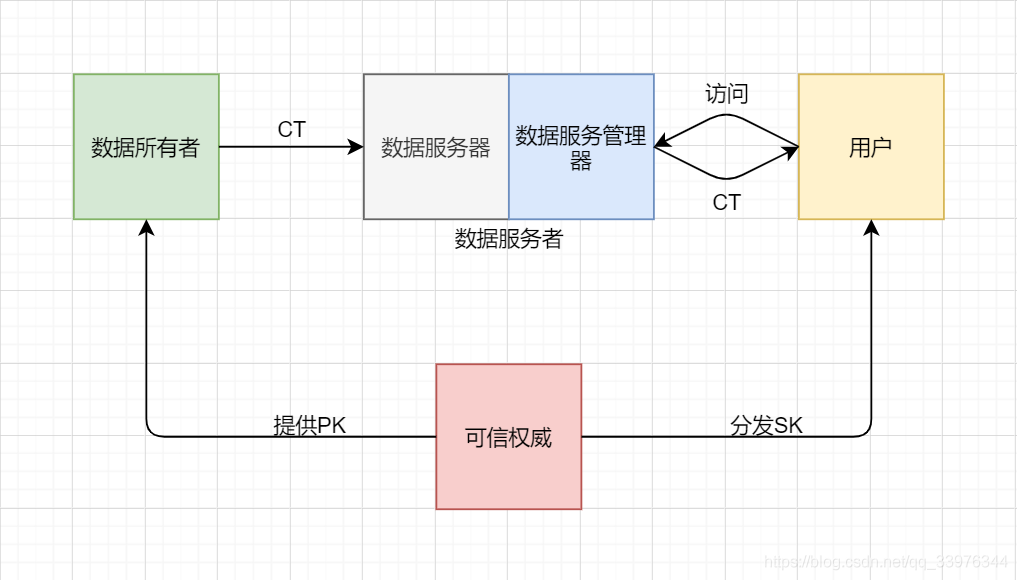
二者对比可以发现，CP-ABE中数据拥有者（加密明文得到密文的人）可以根据自己的需求，定义合适的访问结构，让他所期待的一群用户能够解密，这正好适合构建云环境或者雾环境中数据的安全共享方案，描述的是一对多、多对多的数据共享场景。

ABE的优点是降低公钥管理难度；一次加密、多人共享；一对多、多对多；知道接收群组的规模与总体用户的身份信息即可，无需知道接收方的具体身份信息。
当然，ABE的缺点其实也是显而易见的，只要主密钥泄露，系统也就被完全攻破了。

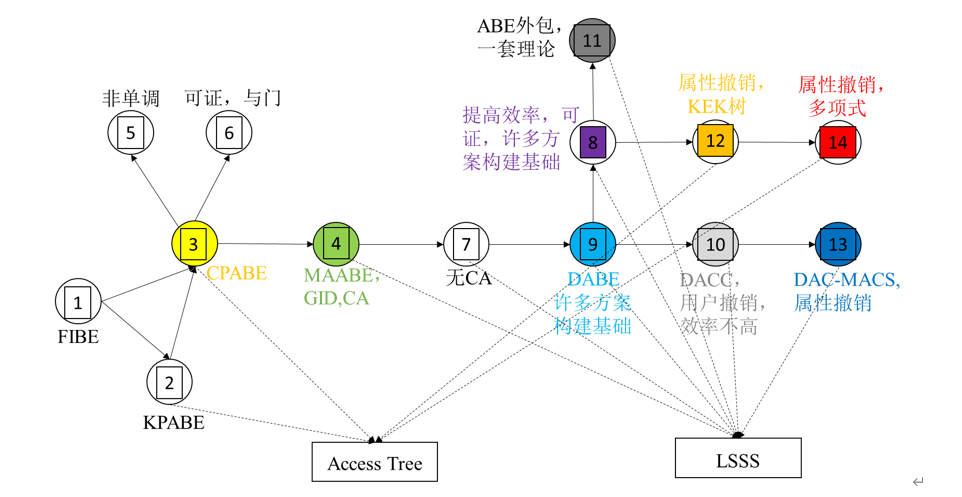
ABE之所以采用主密钥+属性密钥的形式，是为了方便外包以及撤销；而撤销是为了是为了设置有效期，实现访问控制。

双线性映射

双线性映射是基于Diffie-Hellman难题构建属性基加密算法的数学基础，此处的模糊身份基加密也用到了该数学基础。

令\(\mathbb{G}_1,\mathbb{G}_2\)为两个阶为\(p\)的乘法循环群，\(g\)为\(\mathbb{G}_1\)的生成元，一个从\(\mathbb{G}_1\)到\(\mathbb{G}_2\)的映射\(e:\mathbb{G}_1 \times \mathbb{G}_1\rightarrow \mathbb{G}_2\)是双线性的，当其满足以下三点：

• 双线性：\(\forall g, h \in \mathbb{G}_1\)和\(a,b \in \mathbb{Z}_p\)有\(e\left ( g^a, h^b \right ) = e\left ( g, h \right )^{ab}\)；
• 非退化性：\(e\left ( g, h \right ) \neq 1\)；
• 可计算性：\(\forall g, h \in \mathbb{G}_1\)，存在有效的算法计算\(e\left ( g, h \right ) \in \mathbb{G}_2\)。

相关概念：

合数阶群双线性映射

素数阶群双线性映射

补充

• 若\(G_1 \neq G_2\)，称该映射为 非对称双线性映射
• 若\(G_1 = G_2\)，称该映射为 对称双线性映射

单调访问结构

令 \(\left \{ P_1,P_2,…,P_n \right \}\)为一系列参与者的集合（属性基加密里边指的是属性），一个集合\(\mathbb{A} \subseteq 2^ { \left \{ P_1,P_2,…,P_n \right \}}\)是单调的，当其满足：\(\forall B,C\)，如果\(B\in \mathbb{A}\)且\(B\subseteq C\)，则\(C\in \mathbb{A}\)。一个访问结构（单调访问结构）是\(\left \{ P_1,P_2,…,P_n \right \}\)的幂集的非空子集，即\(\mathbb{A} \subseteq 2^ { \left \{ P_1,P_2,…,P_n \right \} \setminus \left \{\varnothing \right \}}\)，在\(\mathbb{A}\)中的集合为授权集合，不在\(\mathbb{A}\)的集合为非授权集合。

例如：假设有用户\(\left\{1,2,3,4\right\}\),只有 \((1,2)\) 合作，或者 \((3,4)\) 合作可以恢复秘密，\((1,3,4)\) 当然也可以恢复秘密，但是 \((1,3,4)\) 不是 \(((1,2),(3,4))\) 的超集。

可以理解为在包含所需要的属性的基础上，包含的属性更多，也依然符合这一访问结构。（即为授权集合）

与门访问结构（And-Gate）

访问控制树（Access Tree）

线性秘密共享（LSSS）

令 \(\mathbb{P}=\left \{ P_1,P_2,…,P_n \right \}\) 为一系列参与者的集合，\(\mathbb{P}\) 上的一个秘密共享方案 \(\prod\) 是线性的，当且仅当满足如下两个条件：

• 每个参与者关于秘密值 \(s\) 的份额构成 \(\mathbb{Z}_{p}\) 上的一给向量；
• 存在一个秘密共享方案 \(\prod\) 的分享生成矩阵 \(M \in \mathbb{Z}_{p} ^ {l \times \theta}\),函数 \(\rho \left ( i \right )\) 将矩阵的第 \(i\) 行映射到一个 \(U\) 上的属性，即 \(\rho \left ( i \right ) \in U, \forall i \in \left [ l \right ]\)。给定一个列向量 \(\overrightarrow{v}=\left ( s,r_2,…,r_{\theta} \right )\)，其中 \(s \in \mathbb{Z}_{p}\)是需要共享的秘密值，\(r_2,…,r_{\theta}\)在\(\mathbb{Z}_{p}\)上随机选取，\(M\overrightarrow{v}\)向量是根据秘密共享方案\(\prod\)的\(l\)份份额，第\(i\)份份额\(\delta _i = \left ( Mv \right )_i\)是属于属性\(\rho \left ( i \right )\)，即为\(M\)和\(\overrightarrow{v}\)的内积。

线性秘密共享方案具有线性重构的特性。假设一个线性秘密共享方案\(\prod\)代表一个访问结构，令\(A \in \mathbb{A}\)表示一个授权的属性集合，索引集合\(I \subset \left \{ 1,…,l \right \}\)定义为\(I=\left \{ i:\rho \left ( i \right ) \in A \right \}\)。根据线性重构的性质，则存在一系列常数的集合\(\left \{ \omega_i \in \mathbb{Z}_p \right \}_{i \in I}\)，使得\(s=\sum _{i \in I} \omega _i\delta _i\)。而且这些常数能在多项式时间内找到。对于任何非授权的集合，找不到满足条件的一组常数。

本质还是矩阵运算。

离散对数难题

令\(\alpha \in \mathbb{Z}_{p}\)，\(G\)为一个乘法循环群，群的阶数为\(p\)，群的一个生成元为\(g\)，离散对数难题说的是：给定\(g,g^a \in G\)，对于任何多项式时间的攻击者，其计算出指数\(a\)的概率是可忽略的，即由\(g,g^a \in G\)计算出\(a\)是困难的。

拉格朗日插值法

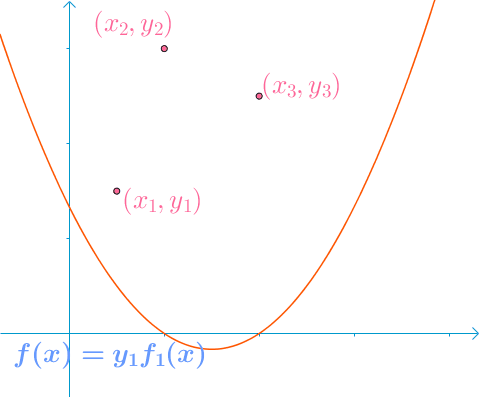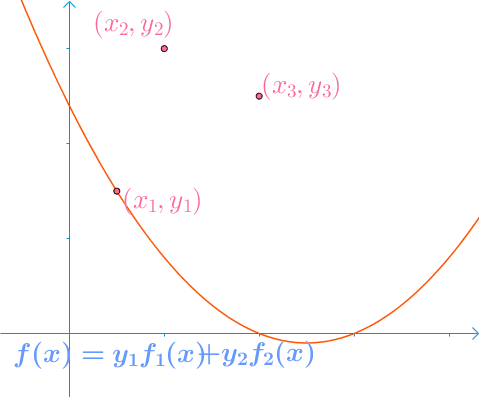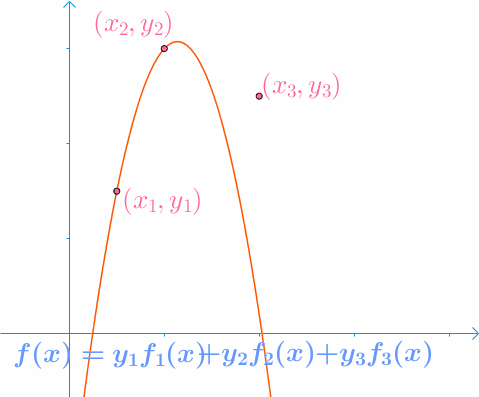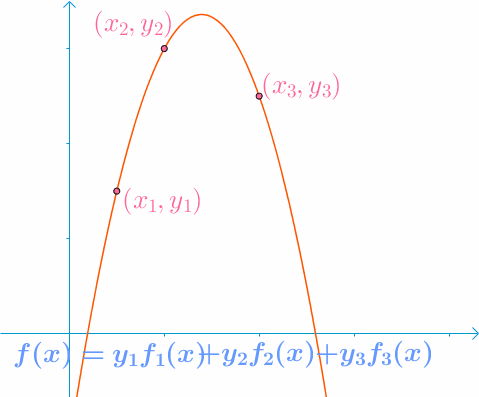
任意给定\(k\)阶多项式函数，已知给定\(k+1\)个取值点（互不重复）：\(\left ( x_0,y_0 \right ),\left ( x_1,y_1 \right ),…,\left ( x_k,y_k \right )\)，其中\(i \neq j\)时\(x_i \neq x_j\)。可以通过以下插值方式恢复多项式：
其中\(l_j\left ( x \right )\)为拉格朗日系数：

\[l_j\left ( x \right )=\prod _{i=0,i\neq j}^k \frac{x-x_i}{x_j-x_i}= \frac{x-x_0}{x_j-x_0}...\frac{x-x_{j-1}}{x_j-x_{j-1}}\cdot \frac{x-x_{j+1}}{x_j-x_{j+1}}...\frac{x-x_k}{x_j-x_k} \]

任意多于\(k+1\)个取值点都能复原多项式。

辅助理解：视频

安全模型（安全游戏/挑战）

• 按照攻击者能力划分：选择明文攻击、选择密文攻击、适应性/非适应性选择密文攻击

• 按照安全目标划分：单向安全性、不可区分安全性、非延展安全性
  模糊身份基加密中是选择身份模型（selective-ID），而属性基加密中是选择集合模型（selective-set）。而且上述模型有两个地方需要注意：

• 在CP-ABE模型没有Init阶段（在模糊身份基加密的模型中有init阶段），称之为选择明文攻击下不可区分安全（IND-CPA）。如果在Init阶段攻击者声明想要挑战的访问结构，则称之为选择安全模型。很显然，选择安全模型描述的安全性弱一些。

• 若是在Phase 1阶段还适应性地查询密文，则称之为适应性选择密文攻击安全模型1（CCA1），若是继续在Phase 2阶段还适应性地查询密文，则称之为适应性选择密文攻击安全模型2（CCA2)。很显然，就安全性而言，IND-CPA、CCA1、CCA2依次增强。

安全性证明

密码学中构建方案，通常将方案的安全性规约到某个数学困难问题，用反证法的思想，当难题是困难的，那么攻破方案就是困难的。FIBE方案是在选择身份模型下将方案规约到MBDH问题。（除此之外还有DL、BDH、DBDH等安全假设）。

Waters论文中详细介绍了三种具体方案的构造，但是前两种被学者们“开发”的多，因此在这里着重介绍前两种。第一种基于Decisional q-PBDHE困难假设，第二种基于BDHE假设。无论是哪一种构造，方案的安全模型是和CP-ABE里边的安全模型是一样的。这些实现都将线性秘密共享（LSSS） 作为访问结构，进而依赖特定的难题，完成安全性的规约证明。

详细请看：关于ABE中的安全性证明

可证明安全理论

• 计算安全性
• 可证明安全性
• 无条件安全性