算法与数据结构实验题 3.11 happiness
实验任务
这一天是小V 的生日,他收到了朋友们送给他的礼物。
现在,小V 有n 件礼物,他将这n 件礼物排成一排,依次编号为1 到n,每件礼物都有一个满意值w[i]。
现在小V 要从中选取连续编号的礼物(即选取[l, r]内的礼物),使得获得的 happiness 最大。
[l, r]内的 happiness 定义为:
小V 想知道他能获得的 happiness 最大是多少,你能帮帮他吗?
数据输入
第一行为一个正整数 n。
第二行为n 个整数 w[1], w[2], …, w[n]
其中:
对于 50%的数据:1<=n<=100, 0<=w[i]<=100
对于 80%的数据:1<=n<=1,000, 0<=w[i]<=1,000
对于 100%的数据:1<=n<=100,000, 0<=w[i]<=10,000
数据输出
小 V能获得的最大 happiness值。
输入示例1
3
1 2 3
输出示例1
10
输入示例2
3
2 1 3
输出示例2
9
代码一
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int inf=2e9+1;
int n,a[100010],l[100010],r[100010];
ll ans,sum[100010];
stack<int>stkl,stkr;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) {
scanf("%d",&a[i]);
sum[i]=sum[i-1]+a[i];
}
for(int i=1;i<=n;i++) {
while(!stkl.empty()&&a[stkl.top()]>=a[i]) stkl.pop();
if(!stkl.empty()) l[i]=stkl.top()+1;
else l[i]=1;
stkl.push(i);
}
for(int i=n;i>=1;i--) {
while(!stkr.empty()&&a[stkr.top()]>=a[i]) stkr.pop();
if(!stkr.empty()) r[i]=stkr.top()-1;
else r[i]=n;
stkr.push(i);
}
for(int i=1;i<=n;i++) ans=max(ans,a[i]*(sum[r[i]]-sum[l[i]-1]));
printf("%lld",ans);
return 0;
}
代码二 · 代码一单栈精简版
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int inf=2e9+1;
int n,i;
stack<ll>s;
ll ans,a[100010],sum[100010];
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++) {
scanf("%lld",&a[i]);
if(i) sum[i]=sum[i-1]+a[i];
else sum[i]=a[i];
}
while(i<=n) {
if(s.empty()||a[s.top()]<=a[i]) s.push(i++);
else {
int t=s.top();
s.pop();
if(s.empty()) ans=max(ans,sum[i-1]*a[t]);
else ans=max(ans,(sum[i-1]-sum[s.top()])*a[t]);
}
}
printf("%lld",ans);
return 0;
}
思路
本题考点为单调栈,应该可以说是这一套课程下来最难的题了
代码一的总体思路讲解如下,代码二即为代码一的简化版,理解难度较大,这里暂不讲解
本体考查一个区间内的最小值和数值之和,数值和自然不用多说,用前缀和解决即可,现在的问题在于,区间最小值该如何实现?
我们从一个例子来入手:
7
1 2 3 5 4 1 2
假设我们用数组 \(l\) 来表示区间的开始位置,用数组 \(r\) 来表示区间的结束位置,那么接下来的问题就是,怎么填充 \(l\) 、\(r\) 数组,来使得 \(l\) \(r\) 区间取得 \(最小值 \times 总和\) 的最大值;换个角度说,就是怎么求出 \(a[i]\) 所对应的 \(l[i]\) 、 \(r[i]\) ,使得 \(a[i]\) 在这个范围内是最小值。
用最简单暴力的思路想,就是对于每一个 \(a[i]\) ,我们都暴力往后查找,直到找到比他小的数为止,但很显然这是必然会超时的,但总体思路来说是正确的。
思考一下,当我们取得最大值时,如果第1个“1”在我们所考虑的区间之内,那么第6个“1”也必然在,因此囊括在两个“1”区间的元素在最小值不变的情况下,取得了总和的最大值,这就是一个区间内的最优解,那我们要怎么去向这个最优解靠拢呢?
我们翻译一下刚刚思考的过程,如果 \(l\) 此时取 6 ,那么我们就应该把他改成 1 ,以此来取得区间的最优开始点,其中需要保持两个“1”之间没有比 1 更小的数,因此此时生成的 \(l\) 数组,就是从 \(l[i]\) 开始时,区间内的最小值为 \(a[i]\)
所以, \(l\) 数组所代表的,就是你从 \(i\) 开始,不如从 \(l[i]\) 开始,此时区间内的最小值为 \(a[i]\);同理, \(r\) 数组所代表的,就是你以 \(i\) 结束,不如以 \(r[i]\) 结束,此时区间内的最小值为 \(a[i]\);二者结合,意思就是在 \(l[i]\) 与 \(r[i]\) 之间的最小值为 \(a[i]\) ,以此取得最优解。
以上的分析过后,\(l\) 、\(r\) 数组取值如下:
\(a = [1,2,3,5,4,1,2]\)
\(l = [1,2,3,4,4,1,7]\)
\(r = [6,5,5,4,5,6,7]\)
可以发现,当单调递增时, \(l[i]\) 单调递增,与 \(i\) 保持一致,否则与上一个大于等于自己的 \(l[i]\) 一致,当重新回到单调递增时, \(l[i]\) 开始重新轮回。 \(r[i]\) 此时也同理,只不过为倒序。这样首尾相接保持联系的状态很适合用这个单元的内容——栈,来解决。
下图形象地展示了这个过程:
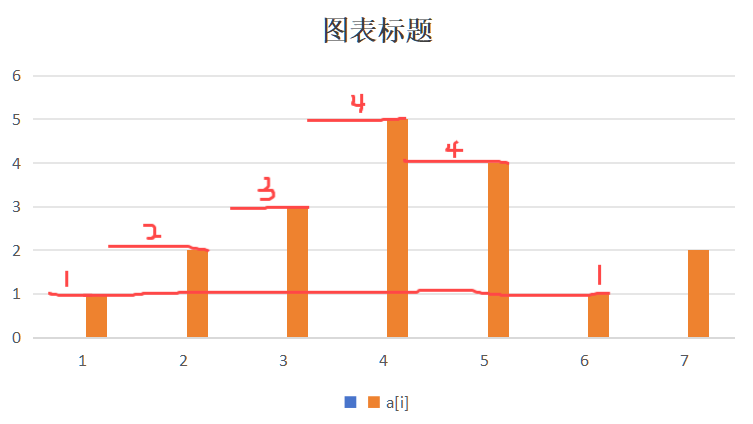
因此在程序中,我们采用栈的方式来保持栈首与栈尾之间的数不超过他们,此时栈首也就是 \(l[i]\) 的取值了
for(int i=1;i<=n;i++) {
while(!stkl.empty()&&a[stkl.top()]>=a[i]) stkl.pop();
if(!stkl.empty()) l[i]=stkl.top()+1;
else l[i]=1;
stkl.push(i);
}
\(r[i]\) 的道理也同上,具体参见代码。
终 于 写 完 了



 浙公网安备 33010602011771号
浙公网安备 33010602011771号