Huff曲线

题目:

from Crypto.Util.number import *
from random import randint
from secret import flag,order

class CB_curve:
    def __init__(self):
        self.p = 1141741939958844590498346884870015122543626602665954681008204697160652371664923
        self.a = 727131475903635498678013730344448225340496007388151739960305539398192321065043
        self.b = 840714623434321649308065401328602364673881568379142278640950034404861312007307

    def add(self, P, Q):
        if P == -1:
            return Q
        (x1, y1) = P
        (x2, y2) = Q
        x3 = (x1+x2)*(1+self.a*y1*y2)*inverse((1+self.b*x1*x2)*(1-self.a*y1*y2),self.p)% self.p
        y3 = (y1+y2)*(1+self.b*x1*x2)*inverse((1-self.b*x1*x2)*(1+self.a*y1*y2),self.p)% self.p
        return (x3, y3)

    def mul(self, x, P):
        Q = -1
        while x > 0:
            if x & 1:
                Q = self.add(Q, P)
            P = self.add(P, P)
            x = x >> 1
        return Q
    
    def negG(self,G):
        return self.mul(order-1,G)

ecc = CB_curve()
G = (586066762126624229327260483658353973556531595840920560414263113786807168248797, 66727759687879628160487324122999265926655929132333860726404158613654375336028)
P = (ecc.mul(bytes_to_long(flag),G)[0],randint(1,ecc.p))
Q = (460843895959181097343292934009653542386784127282375019764638432240505304648101, 739422832583403823403837831802136107593509589942947902014204968923412689379907)

e = randint(1,p)
pl = [ecc.add(P,ecc.mul(10-i,ecc.negG(Q)))[0] + e for i in range(10)]
ph = [ecc.add(P,ecc.mul(10-i,Q))[0] + e for i in range(10)]

print(pl)
print(ph)
#pl = [908996880816674413953945844149350915331956247471480600840221415119794882139724, 971918808384910355828135603762747020183688585728289421786279444571287619529246, 1285550352531583269956802123237391199017403081800977678246201935580429758051904, 1551774945769448705387900437472951015954157193946719575845523359198154668857591, 676185408751480221545400062950292727848016906516506232986883519673765317932582, 1250300209784131850574858927023046353058343552115735540789593580037130054384362, 1298409778422699298367007023890818793557023853717180295526932023194697263501748, 1332552452292482549702793642987623159617988974910321945878093492007278710993114, 1030239404875082841481045525469865919289388171602293245905162820968158543176773, 1154148024180033719999293176590867264297899817449945744942661351655533433871621]
#ph = [584297112520340495757457954416165393828472756298945167299482077258411155766756, 886432149227960827335266910774569034430464592640209168563805700117347063152246, 613528590036968449893421430816319461615130635882647544978722093413694101540550, 576162106332135829961234799085370038425761945928004579456101802617485243023987, 627570890346195626159365118862437334953500165050236216404858019114288681512171, 1015503424232985454098149884321288932492551183126601131968495641510550575005042, 1532737675157046782602115678180407262847166210963507805526455422934164759886583, 1540047002602145805476906585925538790245968214992837106009502002588479779602195, 505097517314409449404205152068185149808364887623922221197462411159844816865696, 873498218680784138428154510303205366133389839886911286745954821800632158315951]

解题思路:

分析曲线

其曲线一般方程为

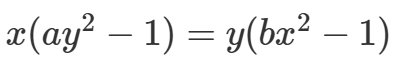![](https://cdn.nlark.com/yuque/0/2025/png/49294098/1743162718078-e99d0fd3-eb6d-44a8-a37a-eb2a3d3105a9.png)

分析曲线结构

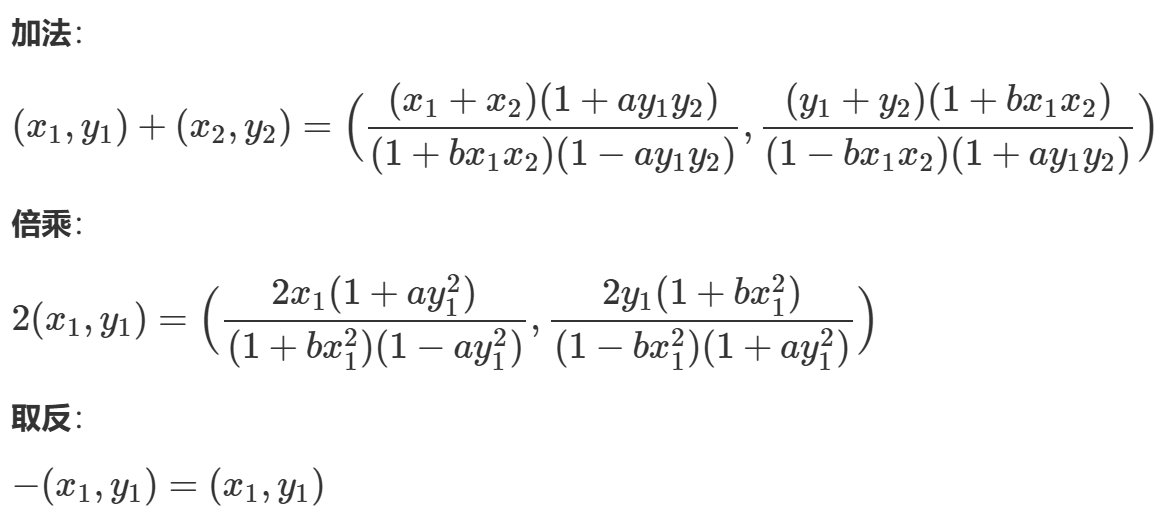
分析代码

**p**:模数,表示椭圆曲线定义在有限域Fp上
**a**和**b**:椭圆曲线的参数,用于定义曲线的方程
**P**:是通过flag转换为整数后与生成元G相乘得到的点
**Q**:是一个固定的点
**e**:随机数,用于混淆
**negG(self, G)**:计算生成元G的负点
- 通过order - 1与G相乘来得到G的负点
**pl**和**ph**:通过椭圆曲线操作生成两组混淆后的点
- **pl**是通过P+(10−i)×(−Q)计算得到的点的x坐标,加上随机数e
- **ph**是通过P+(10−i)×Q计算得到的点的x坐标,加上随机数e

解答:

首先这个式子有3个未知数x,y,e
通过ph可以得到10组关于P和e的等式,可以用Groebner基直接出,但是发现这样求的P却不符合曲线方程,求得y是不对的,得将x带入曲线方程再解出y

Q = (460843895959181097343292934009653542386784127282375019764638432240505304648101, 739422832583403823403837831802136107593509589942947902014204968923412689379907)
ph = [584297112520340495757457954416165393828472756298945167299482077258411155766756, 886432149227960827335266910774569034430464592640209168563805700117347063152246, 613528590036968449893421430816319461615130635882647544978722093413694101540550, 576162106332135829961234799085370038425761945928004579456101802617485243023987, 627570890346195626159365118862437334953500165050236216404858019114288681512171, 1015503424232985454098149884321288932492551183126601131968495641510550575005042, 1532737675157046782602115678180407262847166210963507805526455422934164759886583, 1540047002602145805476906585925538790245968214992837106009502002588479779602195, 505097517314409449404205152068185149808364887623922221197462411159844816865696, 873498218680784138428154510303205366133389839886911286745954821800632158315951]
p = 1141741939958844590498346884870015122543626602665954681008204697160652371664923
a = 727131475903635498678013730344448225340496007388151739960305539398192321065043
b = 840714623434321649308065401328602364673881568379142278640950034404861312007307
class CB_curve:
    def __init__(self, p, a, b):
        self.p = p
        self.a = a
        self.b = b

    def add(self, P, Q):
        if P == -1:
            return Q
        (x1, y1) = P
        (x2, y2) = Q
        x3 = (x1 + x2) * (1 + self.a * y1 * y2) * inverse_mod((1 + self.b * x1 * x2) * (1 - self.a * y1 * y2), self.p) % self.p
        y3 = (y1 + y2) * (1 + self.b * x1 * x2) * inverse_mod((1 - self.b * x1 * x2) * (1 + self.a * y1 * y2), self.p) % self.p
        return (x3, y3)

    def mul(self, x, P):
        Q = -1
        while x > 0:
            if x & 1:
                Q = self.add(Q, P)
            P = self.add(P, P)
            x = x >> 1
        return Q
ecc = CB_curve(p, a, b)
Ql=[]
for i in range(10):
    Ql.append(ecc.mul(10-i,Q))
R.<x1,y1,e>=Zmod(p)[]
f=[]
for i in range(len(Ql)):
    x2,y2=Ql[i]
    fi=(ph[i]-e)*(1+b*x1*x2)*(1-a*y1*y2)-(x1+x2)*(1+a*y1*y2)
    f.append(fi)
Ideal(f).groebner_basis()
'''
[x1 + 239643535167901657800210470774814532510308869595840873642845564328410464397042, y1 + 146109242247186884695587727086539555907710369392694609972293964300672819401615, e + 716700711017198421972376297958894204723153539777056104579499803899129208364755]
x = 239643535167901657800210470774814532510308869595840873642845564328410464397042√
y = 146109242247186884695587727086539555907710369392694609972293964300672819401615×
e = 716700711017198421972376297958894204723153539777056104579499803899129208364755√
'''

根据官方wp可知这个x可以消去
https://test-cuycc6s9lprw.feishu.cn/docx/T7budbiSWoTNd4xQGVicHL1Vnpf

p = 1141741939958844590498346884870015122543626602665954681008204697160652371664923
a = 727131475903635498678013730344448225340496007388151739960305539398192321065043
b = 840714623434321649308065401328602364673881568379142278640950034404861312007307
Q = (460843895959181097343292934009653542386784127282375019764638432240505304648101, 739422832583403823403837831802136107593509589942947902014204968923412689379907)
pl = [908996880816674413953945844149350915331956247471480600840221415119794882139724, 971918808384910355828135603762747020183688585728289421786279444571287619529246, 1285550352531583269956802123237391199017403081800977678246201935580429758051904, 1551774945769448705387900437472951015954157193946719575845523359198154668857591, 676185408751480221545400062950292727848016906516506232986883519673765317932582, 1250300209784131850574858927023046353058343552115735540789593580037130054384362, 1298409778422699298367007023890818793557023853717180295526932023194697263501748, 1332552452292482549702793642987623159617988974910321945878093492007278710993114, 1030239404875082841481045525469865919289388171602293245905162820968158543176773, 1154148024180033719999293176590867264297899817449945744942661351655533433871621]
ph = [584297112520340495757457954416165393828472756298945167299482077258411155766756, 886432149227960827335266910774569034430464592640209168563805700117347063152246, 613528590036968449893421430816319461615130635882647544978722093413694101540550, 576162106332135829961234799085370038425761945928004579456101802617485243023987, 627570890346195626159365118862437334953500165050236216404858019114288681512171, 1015503424232985454098149884321288932492551183126601131968495641510550575005042, 1532737675157046782602115678180407262847166210963507805526455422934164759886583, 1540047002602145805476906585925538790245968214992837106009502002588479779602195, 505097517314409449404205152068185149808364887623922221197462411159844816865696, 873498218680784138428154510303205366133389839886911286745954821800632158315951]
xq = Q[0]

class CB_curve:
    def __init__(self):
        self.p = 1141741939958844590498346884870015122543626602665954681008204697160652371664923
        self.a = 727131475903635498678013730344448225340496007388151739960305539398192321065043
        self.b = 840714623434321649308065401328602364673881568379142278640950034404861312007307

    def add(self, P, Q):
        if P == -1:
            return Q
        (x1, y1) = P
        (x2, y2) = Q
        x3 = (x1+x2)*(1+self.a*y1*y2)*inverse_mod((1+self.b*x1*x2)*(1-self.a*y1*y2),self.p)% self.p
        y3 = (y1+y2)*(1+self.b*x1*x2)*inverse_mod((1-self.b*x1*x2)*(1+self.a*y1*y2),self.p)% self.p
        return (x3, y3)

    def mul(self, x, P):
        Q = -1
        x = x % self.p
        while x > 0:
            if x & 1:
                Q = self.add(Q, P)
            P = self.add(P, P)
            x = x >> 1
        return Q
    
    def negG(self,G):
        return self.mul(order-1,G)

ecc = CB_curve()
PR.<e,k,P0> =PolynomialRing(Zmod(p))
f = []
for i in range(10):
    x1 = P0
    x2 = ecc.mul(10-i,Q)[0]
    f.append(x1^2-x2^2-(1-b^2*x1^2*x2^2)*(ph[i]-e)*(pl[i]-e))
ans=Ideal(f).groebner_basis()
print(ans)
'''
[P0^2 + 219493165434454878473973957507132663767650700404392831423708684433961924200902, e + 716700711017198421972376297958894204723153539777056104579499803899129208364755]
y = 219493165434454878473973957507132663767650700404392831423708684433961924200902
e = 716700711017198421972376297958894204723153539777056104579499803899129208364755
'''

现在知道了y和e,我们可求P[0]和x

R.<P0> = PolynomialRing(GF(p))
f = P0^2+219493165434454878473973957507132663767650700404392831423708684433961924200902
print(f.roots())
'''
[(902098404790942932698136414095200590033317733070113807365359132832241907267881, 1), (239643535167901657800210470774814532510308869595840873642845564328410464397042, 1)]
P[0] = 902098404790942932698136414095200590033317733070113807365359132832241907267881
x = 239643535167901657800210470774814532510308869595840873642845564328410464397042
'''

知道P[0]后可以求P[1]

p = 1141741939958844590498346884870015122543626602665954681008204697160652371664923
a = 727131475903635498678013730344448225340496007388151739960305539398192321065043
b = 840714623434321649308065401328602364673881568379142278640950034404861312007307
G = (460843895959181097343292934009653542386784127282375019764638432240505304648101, 739422832583403823403837831802136107593509589942947902014204968923412689379907)

E = EllipticCurve(GF(p),[0,a+b,0,a*b,0])

def mapping(G):
    x,y = G
    x,y = ((b*x-a*y)*inverse_mod(y-x,p)%p,(b-a)*inverse_mod(y-x,p)%p)
    G = E(x,y)
    return G
    
x = 902098404790942932698136414095200590033317733070113807365359132832241907267881  
R.<y> = PolynomialRing(GF(p))
f = x*(a*y^2-1)-y*(b*x^2-1)
y = int(f.roots()[1][0])

P = (x,y)
print(P)
#(902098404790942932698136414095200590033317733070113807365359132832241907267881, 672929595307990944197873882889709005621738844588134711458648048321447534353147)

再换元映射,将huff映射到Weierstrass上来

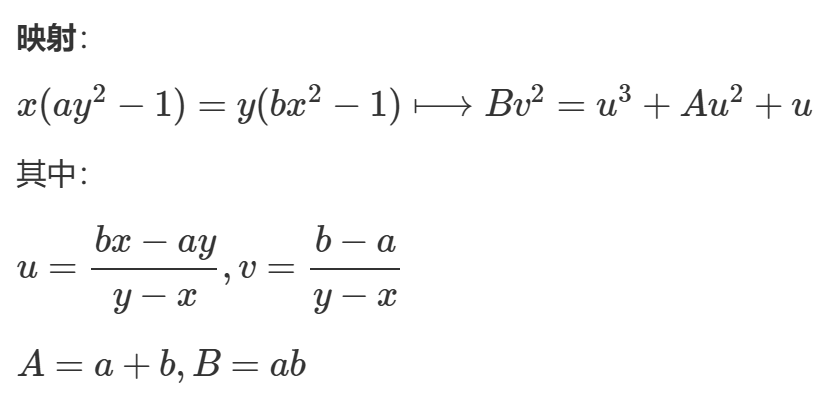
class CB_curve:
    def __init__(self):
        self.p = 1141741939958844590498346884870015122543626602665954681008204697160652371664923
        self.a = 727131475903635498678013730344448225340496007388151739960305539398192321065043
        self.b = 840714623434321649308065401328602364673881568379142278640950034404861312007307

    def add(self, P, Q):
        if P == -1:
            return Q
        (x1, y1) = P
        (x2, y2) = Q
        x3 = (x1+x2)*(1+self.a*y1*y2)*inverse_mod((1+self.b*x1*x2)*(1-self.a*y1*y2),self.p)% self.p
        y3 = (y1+y2)*(1+self.b*x1*x2)*inverse_mod((1-self.b*x1*x2)*(1+self.a*y1*y2),self.p)% self.p
        return (x3, y3)

    def mul(self, x, P):
        Q = -1
        while x > 0:
            if x & 1:
                Q = self.add(Q, P)
            P = self.add(P, P)
            x = x >> 1
        return Q
    
    def negG(self,G):
        return self.mul(order-1,G)
ecc = CB_curve()
p = 1141741939958844590498346884870015122543626602665954681008204697160652371664923
a = 727131475903635498678013730344448225340496007388151739960305539398192321065043
b = 840714623434321649308065401328602364673881568379142278640950034404861312007307
G = (586066762126624229327260483658353973556531595840920560414263113786807168248797, 66727759687879628160487324122999265926655929132333860726404158613654375336028)
P=(902098404790942932698136414095200590033317733070113807365359132832241907267881, 672929595307990944197873882889709005621738844588134711458648048321447534353147)
Q = (460843895959181097343292934009653542386784127282375019764638432240505304648101, 739422832583403823403837831802136107593509589942947902014204968923412689379907)
E = EllipticCurve(GF(p),[0,a+b,0,a*b,0])
print(E)

g = ((b*G[0] - a*G[1]) * inverse_mod(G[1]-G[0],p)%p,(b-a)*inverse_mod(G[1]-G[0],p)%p)
q = ((b*P[0] - a*P[1]) * inverse_mod(P[1]-P[0],p)%p,(b-a)*inverse_mod(P[1]-P[0],p)%p)
G = E(g)
Q = E(q)
print(G)
print(Q)
print(E.order())
'''
Elliptic Curve defined by y^2 = x^3 + 426104159379112557487732246803035467470750973101339337593050876642401261407427*x^2 + 91530605704782235055514790954057524984830206414334253565339948144004385061851*x over Finite Field of size 1141741939958844590498346884870015122543626602665954681008204697160652371664923
(401213088171030363584018990938949410304970540667112434451319358778028859051677 : 460349217535465024866281884380031233781318971872151051532892035527496595213976 : 1)
(682175555764551614570209880595883272089203931371422247526144450729748330692873 : 60260596347572319335133090468745331889659221772219926730100143329656081251910 : 1)
1141741939958844590498346884870015122544171009688372185479632675211885925945760
'''

阶光滑,直接ph就差解出m

n = G.order()
factors, exponents = zip(*factor(n))
primes = [factors[i] ^ exponents[i] for i in range(len(factors))][:-1]
print(primes)
logs=[]
for fac in primes:
    t=int(n)//int(fac)
    log=discrete_log(t*Q,t*G,operation='+')
    logs+=[log]
m = crt(logs,primes)
print(bytes.fromhex(hex(m)[2:]))
'''
[16, 3, 5, 37, 271, 4297, 6983, 9679, 52631, 139571, 84666937, 558977989]
b'DASCTF{goodathuff}'
'''

类似的解法

脚本来自https://www.cnblogs.com/ZimaBlue/articles/17780216.html

from random import randint

class CB_curve:
    def __init__(self):
        self.p = 1141741939958844590498346884870015122543626602665954681008204697160652371664923
        self.a = 727131475903635498678013730344448225340496007388151739960305539398192321065043
        self.b = 840714623434321649308065401328602364673881568379142278640950034404861312007307

    def add(self, P, Q):
        if P == -1:
            return Q
        (x1, y1) = P
        (x2, y2) = Q
        x3 =  (x1+x2)*(1+self.a*y1*y2)*inverse_mod((1+self.b*x1*x2)*(1-self.a*y1*y2),self.p)% self.p
        y3 =  (y1+y2)*(1+self.b*x1*x2)*inverse_mod((1-self.b*x1*x2)*(1+self.a*y1*y2),self.p)% self.p
        return (x3, y3)

    def mul(self, x, P):
        Q = -1
        x = x % self.p
        while x > 0:
            if x & 1:
                Q = self.add(Q, P)
            P = self.add(P, P)
            x = x >> 1
        return Q
    
    def negG(self,G):
        return self.mul(570870969979422295249173442435007561272085504844186092739816337605942962972880-1,G)

ecc = CB_curve()
G = (586066762126624229327260483658353973556531595840920560414263113786807168248797, 66727759687879628160487324122999265926655929132333860726404158613654375336028)
G_ = (-586066762126624229327260483658353973556531595840920560414263113786807168248797, -66727759687879628160487324122999265926655929132333860726404158613654375336028)
Q = (460843895959181097343292934009653542386784127282375019764638432240505304648101, 739422832583403823403837831802136107593509589942947902014204968923412689379907)

# test 
test = (ecc.add(G,G_))
print(test)
q1 = ecc.mul(5,G)
q2 = ecc.mul(5,G_)
print(ecc.add(q1,q2))

# attack
order = 570870969979422295249173442435007561272085504844186092739816337605942962972880
pl = [908996880816674413953945844149350915331956247471480600840221415119794882139724, 971918808384910355828135603762747020183688585728289421786279444571287619529246, 1285550352531583269956802123237391199017403081800977678246201935580429758051904, 1551774945769448705387900437472951015954157193946719575845523359198154668857591, 676185408751480221545400062950292727848016906516506232986883519673765317932582, 1250300209784131850574858927023046353058343552115735540789593580037130054384362, 1298409778422699298367007023890818793557023853717180295526932023194697263501748, 1332552452292482549702793642987623159617988974910321945878093492007278710993114, 1030239404875082841481045525469865919289388171602293245905162820968158543176773, 1154148024180033719999293176590867264297899817449945744942661351655533433871621]
ph = [584297112520340495757457954416165393828472756298945167299482077258411155766756, 886432149227960827335266910774569034430464592640209168563805700117347063152246, 613528590036968449893421430816319461615130635882647544978722093413694101540550, 576162106332135829961234799085370038425761945928004579456101802617485243023987, 627570890346195626159365118862437334953500165050236216404858019114288681512171, 1015503424232985454098149884321288932492551183126601131968495641510550575005042, 1532737675157046782602115678180407262847166210963507805526455422934164759886583, 1540047002602145805476906585925538790245968214992837106009502002588479779602195, 505097517314409449404205152068185149808364887623922221197462411159844816865696, 873498218680784138428154510303205366133389839886911286745954821800632158315951]

a = ecc.a
b = ecc.b
p = ecc.p
R.<xp,e>=PolynomialRing(Zmod(p))
F = []
for i in range(10):
    f = (pl[i] - e) * (ph[i] - e) * (1-b^2*xp^2 * ecc.mul(10-i,Q)[0] ^2) - (xp^2 - ecc.mul(10-i,Q)[0] ^2)
    F.append(f)
res=Ideal(F).groebner_basis()
print(res)
c = -219493165434454878473973957507132663767650700404392831423708684433961924200902
xp = Zmod(p)(c).nth_root(2,all=True)[1]

RR.<yp> = PolynomialRing(Zmod(p))
f = xp*(a*yp^2-1) - yp*(b*xp^2-1)
yp = f.roots()[1][0]

P = (int(xp),int(yp))
E = EllipticCurve(GF(p),[0,a+b,0,a*b,0])
print(E)

g = ((b*G[0] - a*G[1]) * inverse_mod(G[1]-G[0],p)%p,(b-a)*inverse_mod(G[1]-G[0],p)%p)
q = ((b*P[0] - a*P[1]) * inverse_mod(P[1]-P[0],p)%p,(b-a)*inverse_mod(P[1]-P[0],p)%p)

g = E(g)
q = E(q)
# 做映射之后的阶是不会变的

primes = [3 , 5 , 16, 37 , 271 , 4297 , 6983 , 9679 , 52631 , 139571 , 84666937 , 558977989]
logs=[]
for fac in primes:
    t=int(order)//int(fac)
    print('ok')
    log=discrete_log(t*q,t*g,operation='+')
    logs+=[log]
m = crt(logs,primes)
print(bytes.fromhex(hex(m)[2:]))
'''
(0, 0)
(0, 0)
[xp^2 + 219493165434454878473973957507132663767650700404392831423708684433961924200902, e + 716700711017198421972376297958894204723153539777056104579499803899129208364755]
Elliptic Curve defined by y^2 = x^3 + 426104159379112557487732246803035467470750973101339337593050876642401261407427*x^2 + 91530605704782235055514790954057524984830206414334253565339948144004385061851*x over Finite Field of size 1141741939958844590498346884870015122543626602665954681008204697160652371664923
ok
ok
ok
ok
ok
ok
ok
ok
ok
ok
ok
ok
b'DASCTF{goodathuff}'
'''

posted @ 2025-03-28 21:11 sevensnight 阅读(207) 评论(1) 收藏举报

刷新页面返回顶部

SevensNight

Huff曲线

题目:

解题思路:

分析曲线

分析代码

解答:

公告