Edwards曲线

题目:

from Crypto.Util.number import *
from secret import flag, Curve

def ison(C, P):
	c, d, p = C
	x, y = P
	return (x**2 + y**2 - c**2 * (1 + d * x**2*y**2)) % p == 0

def teal(C, P, Q):
	c, d, p = C
	x1, y1 = P
	x2, y2 = Q
	assert ison(C, P) and ison(C, Q)
	x3 = (x1 * y2 + y1 * x2) * inverse(c * (1 + d * x1 * x2 * y1 * y2), p) % p
	y3 = (y1 * y2 - x1 * x2) * inverse(c * (1 - d * x1 * x2 * y1 * y2), p) % p
	return (int(x3), int(y3))

def peam(C, P, m):
	assert ison(C, P)
	c, d, p = C
	B = bin(m)[2:]
	l = len(B)
	x, y = P
	PP = (-x, y)
	O = teal(C, P, PP)
	Q = O
	if m == 0:
		return O
	elif m == 1:
		return P
	else:
		for _ in range(l-1):
			P = teal(C, P, P)
		m = m - 2**(l-1)
		Q, P = P, (x, y)
		return teal(C, Q, peam(C, P, m))

c, d, p = Curve

flag = flag.lstrip(b'CCTF{').rstrip(b'}')
l = len(flag)
lflag, rflag = flag[:l // 2], flag[l // 2:]

s, t = bytes_to_long(lflag), bytes_to_long(rflag)
assert s < p and t < p

P = (398011447251267732058427934569710020713094, 548950454294712661054528329798266699762662)
Q = (139255151342889674616838168412769112246165, 649791718379009629228240558980851356197207)

print(f'ison(C, P) = {ison(Curve, P)}')
print(f'ison(C, Q) = {ison(Curve, Q)}')

print(f'P = {P}')
print(f'Q = {Q}')

print(f's * P = {peam(Curve, P, s)}')
print(f't * Q = {peam(Curve, Q, t)}')

'''
ison(C, P) = True
ison(C, Q) = True
P = (398011447251267732058427934569710020713094, 548950454294712661054528329798266699762662)
Q = (139255151342889674616838168412769112246165, 649791718379009629228240558980851356197207)
s * P = (730393937659426993430595540476247076383331, 461597565155009635099537158476419433012710)
t * Q = (500532897653416664117493978883484252869079, 620853965501593867437705135137758828401933)
'''

解题思路:

分析曲线

  • 我们首先分析这个曲线方程的形式为一个标准爱德华曲线方程

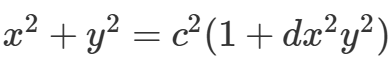
  • 分析曲线结构

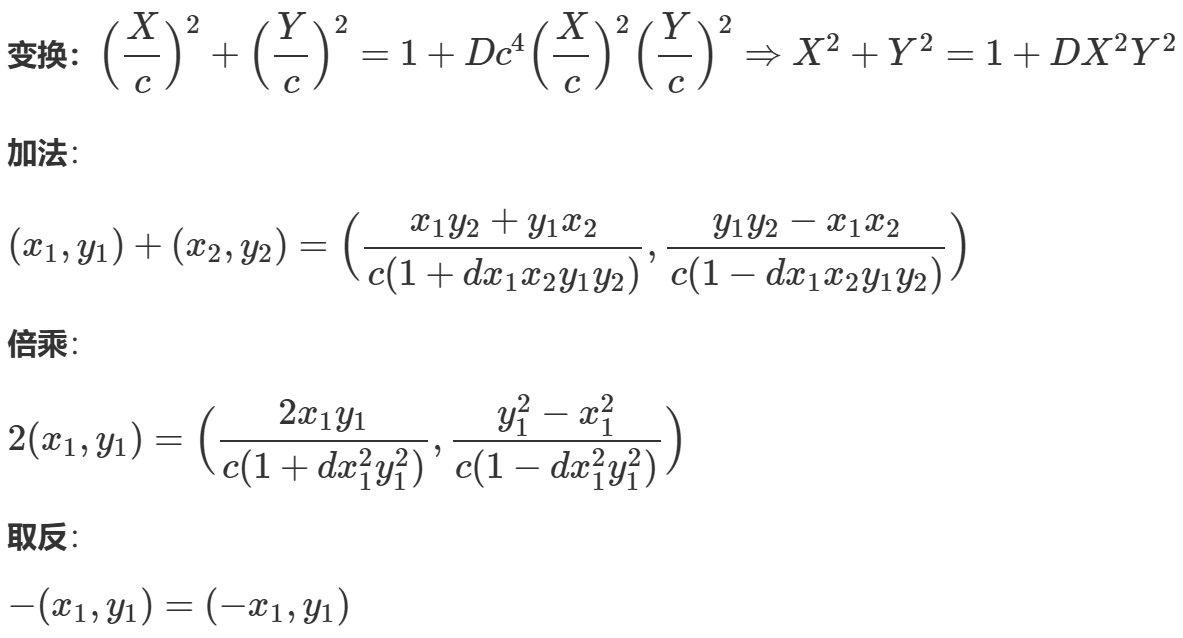
分析代码

  • **p**:模数,表示椭圆曲线定义在有限域Fp上
  • **d**:椭圆曲线的参数,用于定义曲线的方程
  • **c**:缩放因子,用于调整曲线的形状

(上面的参数都在元组里(就是没给,只知道个点))

ison(C,P)函数

  • 这个函数的作用是判断一个点P是否在给定的爱德华曲线上
  • 输入:曲线参数C=(c,d,p)和点P=(x,y)
  • 输出:布尔值,表示点P是否满足爱德华曲线的方程
  • 函数的实现是将点P的坐标代入曲线方程:x^2+y^2-c^2(1+dx^2y^2)≡0(mod p)如果结果为0,则 点P在曲线上,返回True;否则返回False

teal(C,P,Q)函数

  • 这个函数的作用是计算爱德华曲线上两个点P和Q的加法运算
  • 输入:曲线参数C=(c,d,p)和两个点P=(x1,y1)和Q=(x2,y2)
  • 输出:点R=(x3,y3),表示P+Q

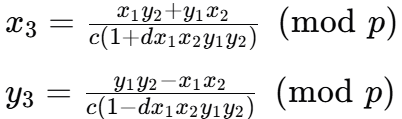
peam(C,P,m)函数

  • 这个函数的作用是计算爱德华曲线上点P的标量乘法,即m×P,标量乘法是椭圆曲线密码学中的核心运算,用于生成公钥和签名等
  • 输入:曲线参数C=(c,d,p),点P=(x,y)和标量m
  • 输出:点R,表示m×P
  • 函数的实现采用了双倍加法算法(Double-and-Add),这是一种高效的标量乘法算法,具体步骤如下:

将标量m转换为二进制表示

从最高位开始,逐位处理m的每一位

- 先将当前点`P`自身相加(即`P=P+P`)
- 如果当前位为`1`,则将`P`加到结果`Q`上

最终返回结果Q

(该代码计算了s×P和t×Q,并输出结果)

  • flag是一个需要加密的标志,被分割为两部分lflag和rflag,分别转换为整数s和t
  • 点P和Q是爱德华曲线上的两个已知点

解密思路1

  • 解密过程需要找到私钥<font style="color:rgb(6, 6, 7);">d</font>,使得<font style="color:rgb(6, 6, 7);">d × e ≡ 1 (mod n)</font>,其中<font style="color:rgb(6, 6, 7);">n</font>是椭圆曲线的阶
  • 那么如何求阶呢,似乎没有办法直接求这种圆锥曲线的阶,不过我们可以将Edcurve通过换元映射,变换为常见的椭圆曲线的形式
换元映射

  • 第一步:转化为蒙哥马利曲线方程(Montgomery)

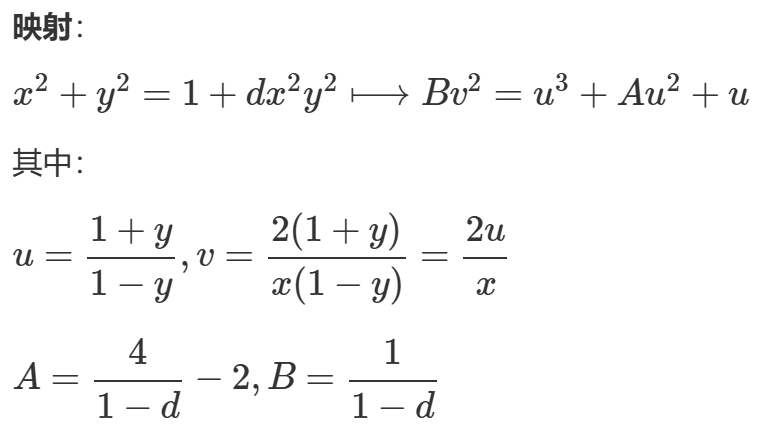     ![](https://cdn.nlark.com/yuque/0/2025/png/49294098/1742740769303-a1b69c05-dd80-4616-b4b3-81af3d87ef71.png)

  • 第二步:转化为椭圆曲线方程(Weierstrass)

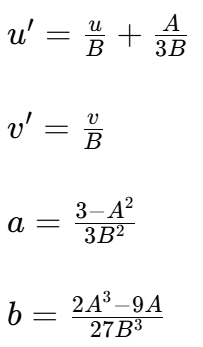
  • 此时蒙哥马利曲线就变成了椭圆曲线方程形式

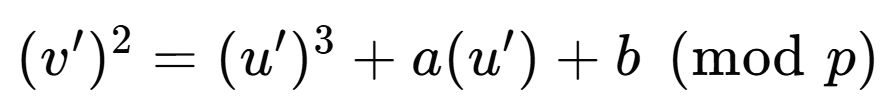     ![](https://cdn.nlark.com/yuque/0/2025/png/49294098/1739692113095-16b94fe0-11f5-41d7-be17-aa894404ecc5.png)

  • 然后求该曲线的阶,并且重新逆变换回Edcurve,得到的横坐标即为flag

解密思路2

求解参数
  • 我们可以直接把曲线的参数求出来
  • 我们的目标是恢复(c,d,p),以便我们可以重建曲线并解决离散对数问题,我们首先将获得p,这将使我们能够进行模p的求逆,从而恢复c,d
  • 求参数的原理参考https://blog.cryptohack.org/cryptoctf2021-hard#rohald
换元映射
  • 参考方法1

解答:

解法1:

def to_elliptic_2(P, p, c, d):
    Zp = Zmod(p)
    x, y = P
    x, y = Zp(x), Zp(y)
    c, d = Zp(c), Zp(d)
    x, y = x * c ** -1, y * c ** -1
    d = d * c ** 4
    u, v = (1 + y) / (1 - y), (2 * (1+y)) / (x * (1-y))

    # Montgomery
    B = 1 / (1-d)
    A = 2 * (1+d) / (1-d)

    # Weierstrass
    x = u / B + A / (3*B)
    y = v / B
    a = (3 - A**2) / (3 * B**2)
    b = (2 * A**3 - 9*A) / (27 * B**3)
    return (x, y), a, b

p = 903968861315877429495243431349919213155709
c = 662698094423288904843781932253259903384619
d = 540431316779988345188678880301417602675534
P = (398011447251267732058427934569710020713094, 548950454294712661054528329798266699762662)
Q = (139255151342889674616838168412769112246165, 649791718379009629228240558980851356197207)
S = (730393937659426993430595540476247076383331, 461597565155009635099537158476419433012710)
T = (500532897653416664117493978883484252869079, 620853965501593867437705135137758828401933)

P1, a, b = to_elliptic_2(P, p, c, d)
Q1, a, b = to_elliptic_2(Q, p, c, d)
S1, a, b = to_elliptic_2(S, p, c, d)
T1, a, b = to_elliptic_2(T, p, c, d)

EC = EllipticCurve(Zmod(p), [a, b])
P1 = EC(P1)
Q1 = EC(Q1)
S1 = EC(S1)
T1 = EC(T1)

s = P1.discrete_log(S1)
t = Q1.discrete_log(T1)
print(s)
print(t)
print(bytes.fromhex(hex(s)[2:])+bytes.fromhex(hex(t)[2:]))
'''
37536673610448804706158374243358240879730
23292556478798423635566146051309141390899
b'nOt_50_3a5Y_Edw4rDs_3LlipT!c_CURv3'
'''
#CCTF{nOt_50_3a5Y_Edw4rDs_3LlipT!c_CURv3}

解法2:

求参数

from math import gcd

def ison(C, P):
    """
    Verification points are on the curve
    """
    c, d, p = C
    u, v = P
    return (u**2 + v**2 - cc * (1 + d * u**2*v**2)) % p == 0

def a_and_b(u1,u2,v1,v2):
    """
    Helper function used to simplify calculations
    """
    a12 = u1**2 - u2**2 + v1**2 - v2**2
    b12 = u1**2 * v1**2 - u2**2 * v2**2
    return a12, b12

def find_modulus(u1,u2,u3,u4,v1,v2,v3,v4):
    """
    Compute the modulus from four points
    """
    a12, b12 = a_and_b(u1,u2,v1,v2)
    a13, b13 = a_and_b(u1,u3,v1,v3)
    a23, b23 = a_and_b(u2,u3,v2,v3)
    a24, b24 = a_and_b(u2,u4,v2,v4)

    p_almost = gcd(a12*b13 - a13*b12, a23*b24 - a24*b23)

    for i in range(2,1000):
        if p_almost % i == 0:
            p_almost = p_almost // i

    return p_almost

def c_sq_d(u1,u2,v1,v2,p):
    """
    Helper function to computer c^2 d
    """
    a1,b1 = a_and_b(u1,u2,v1,v2)
    return a1 * pow(b1,-1,p) % p

def c(u1,u2,v1,v2,p):
    """
    Compute c^2, d from two points and known modulus
    """
    ccd = c_sq_d(u1,u2,v1,v2,p)
    cc = (u1**2 + v1**2 - ccd*u1**2*v1**2) % p
    d = ccd * pow(cc, -1, p) % p
    return cc, d


P = (398011447251267732058427934569710020713094, 548950454294712661054528329798266699762662)
Q = (139255151342889674616838168412769112246165, 649791718379009629228240558980851356197207)
sP = (730393937659426993430595540476247076383331, 461597565155009635099537158476419433012710)
tQ = (500532897653416664117493978883484252869079, 620853965501593867437705135137758828401933)

u1, v1 = P
u2, v2 = Q
u3, v3 = sP
u4, v4 = tQ

p = find_modulus(u1,u2,u3,u4,v1,v2,v3,v4)
cc, d = c(u1,u2,v1,v2,p)

C = cc, d, p
assert ison(C, P)
assert ison(C, Q)
assert ison(C, sP)
assert ison(C, tQ)

print(f'Found curve parameters')
print(f'p = {p}')
print(f'c^2 = {cc}')
print(f'd = {d}')
'''
Found curve
p = 903968861315877429495243431349919213155709
c^2 = 495368774702871559312404847312353912297284
d = 540431316779988345188678880301417602675534
'''

换元映射

def to_elliptic_2(P, p, c, d):
    Zp = Zmod(p)
    x, y = P
    x, y = Zp(x), Zp(y)
    c, d = Zp(c), Zp(d)
    x, y = x / c , y / c 
    d = d * c ** 4
    
    # Montgomery
    u = (1 + y) / (1 - y)
    v = (2 * (1+y)) / (x * (1-y))
    B = 1 / (1-d)
    A = 2 * (1+d) / (1-d)

    # Weierstrass
    x = u / B + A / (3*B)
    y = v / B
    a = (3 - A**2) / (3 * B**2)
    b = (2 * A**3 - 9*A) / (27 * B**3)
    return (x, y), a, b

p = 903968861315877429495243431349919213155709
c = 662698094423288904843781932253259903384619
d = 540431316779988345188678880301417602675534
P = (398011447251267732058427934569710020713094, 548950454294712661054528329798266699762662)
Q = (139255151342889674616838168412769112246165, 649791718379009629228240558980851356197207)
S = (730393937659426993430595540476247076383331, 461597565155009635099537158476419433012710)
T = (500532897653416664117493978883484252869079, 620853965501593867437705135137758828401933)

P1, a, b = to_elliptic_2(P, p, c, d)
Q1, a, b = to_elliptic_2(Q, p, c, d)
S1, a, b = to_elliptic_2(S, p, c, d)
T1, a, b = to_elliptic_2(T, p, c, d)

EC = EllipticCurve(Zmod(p), [a, b])
P1 = EC(P1)
Q1 = EC(Q1)
S1 = EC(S1)
T1 = EC(T1)

s = P1.discrete_log(S1)
t = Q1.discrete_log(T1)
print(s)
print(t)
print(bytes.fromhex(hex(s)[2:])+bytes.fromhex(hex(t)[2:]))
'''
Share
37536673610448804706158374243358240879730
23292556478798423635566146051309141390899
b'nOt_50_3a5Y_Edw4rDs_3LlipT!c_CURv3'
'''
#CCTF{nOt_50_3a5Y_Edw4rDs_3LlipT!c_CURv3}
posted @ 2025-03-23 23:02  sevensnight  阅读(45)  评论(0)    收藏  举报