背包密码密度的作用(LLL算法的实现)
背包问题通解:
当密度d满足以下条件时,LLL算法能有效地解决这类背包问题
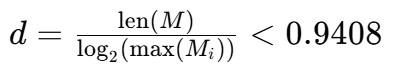
其中:
- len(M)是向量M的长度,即向量中元素的数量
- max(Mi)是向量M中的最大元素
计算:
import math
def calculate_density(M):
if all(isinstance(sub_list, list) for sub_list in M): #检查 M 是否为二维列表
densities = []
for sub_list in M:
len_M = len(sub_list) #计算子列表的长度
max_Mi = max(sub_list) #找到子列表中的最大元素
density = len_M / math.log2(max_Mi)
densities.append(density)
return densities
else:
len_M = len(M) #计算列表的长度
max_Mi = max(M) #找到列表中的最大元素
return len_M / math.log2(max_Mi)
#M_single = []
#M_multiple = [[],[],[]]
#计算单个背包问题的密度
density_single = calculate_density(M_single)
print(f"单个背包的密度是: {density_single}")
#计算多个背包问题的密度
densities_multiple = calculate_density(M_multiple)
for i, density in enumerate(densities_multiple):
print(f"第 {i + 1} 个背包的密度是: {density}")
构造格:
- 定义公钥序列M:
- 公钥序列
<font style="color:rgb(44, 44, 54);">M=(M</font><sub><font style="color:rgb(44, 44, 54);">1</font></sub><font style="color:rgb(44, 44, 54);">,M</font><sub><font style="color:rgb(44, 44, 54);">2</font></sub><font style="color:rgb(44, 44, 54);">,…,M</font><sub><font style="color:rgb(44, 44, 54);">n</font></sub><font style="color:rgb(44, 44, 54);">)</font>,其中每个<font style="color:rgb(44, 44, 54);">M</font><sub><font style="color:rgb(44, 44, 54);">i</font></sub>是一个整数
- 公钥序列
- 构造格的基:
- 格的基是一个矩阵,每一行代表一个向量;对于背包问题,可以构造如下矩阵:

- <font style="color:rgb(44, 44, 54);">这里</font>`<font style="color:rgb(44, 44, 54);">S</font>`<font style="color:rgb(44, 44, 54);">是目标值,即背包问题中需要达到的总重量</font>
- 理解每一行向量Vi:
- 每一行向量
<font style="color:rgb(44, 44, 54);">V</font><sub><font style="color:rgb(44, 44, 54);">i</font></sub>的形式为<font style="color:rgb(44, 44, 54);">(1,0,…,0,M</font><sub><font style="color:rgb(44, 44, 54);">i</font></sub><font style="color:rgb(44, 44, 54);">)</font>,表示在第i个位置有一个<font style="color:rgb(44, 44, 54);">M</font><sub><font style="color:rgb(44, 44, 54);">i</font></sub>,其余位置为<font style="color:rgb(44, 44, 54);">0</font>
- 每一行向量
- 明文序列x:
- 明文序列
<font style="color:rgb(44, 44, 54);">x=(x</font><sub><font style="color:rgb(44, 44, 54);">1</font></sub><font style="color:rgb(44, 44, 54);">,x</font><sub><font style="color:rgb(44, 44, 54);">2</font></sub><font style="color:rgb(44, 44, 54);">,…,x</font><sub><font style="color:rgb(44, 44, 54);">n</font></sub><font style="color:rgb(44, 44, 54);">)</font>,其中每个<font style="color:rgb(44, 44, 54);">x</font><sub><font style="color:rgb(44, 44, 54);">i</font></sub>只能取<font style="color:rgb(44, 44, 54);">0</font>或<font style="color:rgb(44, 44, 54);">1</font>,表示是否选择第<font style="color:rgb(6, 6, 7);">i</font>个物品
- 明文序列
- 线性组合:
- 对于线性组合
<font style="color:rgb(44, 44, 54);">x</font><sub><font style="color:rgb(44, 44, 54);">1</font></sub><font style="color:rgb(44, 44, 54);">V</font><sub><font style="color:rgb(44, 44, 54);">1</font></sub><font style="color:rgb(44, 44, 54);">+x</font><sub><font style="color:rgb(44, 44, 54);">2</font></sub><font style="color:rgb(44, 44, 54);">V</font><sub><font style="color:rgb(44, 44, 54);">2</font></sub><font style="color:rgb(44, 44, 54);">+⋯+x</font><sub><font style="color:rgb(44, 44, 54);">n</font></sub><font style="color:rgb(44, 44, 54);">V</font><sub><font style="color:rgb(44, 44, 54);">n</font></sub><font style="color:rgb(44, 44, 54);">−V</font><sub><font style="color:rgb(44, 44, 54);">n+1</font></sub>,这个组合必然在格点上,因为<font style="color:rgb(44, 44, 54);">x</font><sub><font style="color:rgb(44, 44, 54);">i</font></sub>只能取<font style="color:rgb(44, 44, 54);">0</font>或<font style="color:rgb(44, 44, 54);">1</font> - 向量
<font style="color:rgb(44, 44, 54);">t=x</font><sub><font style="color:rgb(44, 44, 54);">1</font></sub><font style="color:rgb(44, 44, 54);">V</font><sub><font style="color:rgb(44, 44, 54);">1</font></sub><font style="color:rgb(44, 44, 54);">+x</font><sub><font style="color:rgb(44, 44, 54);">2</font></sub><font style="color:rgb(44, 44, 54);">V</font><sub><font style="color:rgb(44, 44, 54);">2</font></sub><font style="color:rgb(44, 44, 54);">+⋯+x</font><sub><font style="color:rgb(44, 44, 54);">n</font></sub><font style="color:rgb(44, 44, 54);">V</font><sub><font style="color:rgb(44, 44, 54);">n</font></sub><font style="color:rgb(44, 44, 54);">−V</font><sub><font style="color:rgb(44, 44, 54);">n+1</font></sub>可以表示为<font style="color:rgb(44, 44, 54);">t=(x</font><sub><font style="color:rgb(44, 44, 54);">1</font></sub><font style="color:rgb(44, 44, 54);">,x</font><sub><font style="color:rgb(44, 44, 54);">2</font></sub><font style="color:rgb(44, 44, 54);">,…,x</font><sub><font style="color:rgb(44, 44, 54);">n</font></sub><font style="color:rgb(44, 44, 54);">,0)</font>
- 对于线性组合
- 向量长度和格的体积:
- 向量t的长度
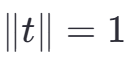
- 格的体积
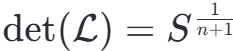
- 向量t的长度
- Hermite定理:
- 根据Hermite定理,
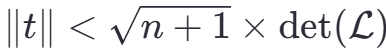
- 根据Hermite定理,
- 最短向量:
- 因此,向量
<font style="color:rgb(44, 44, 54);">t</font>是格L的最短向量,可以用LLL算法来找到它
- 因此,向量
代码实现:
使用整数环**ZZ**来构造矩阵A
c=
pub=[]
nbit = len(pub)
A = Matrix(ZZ, nbit + 1, nbit + 1)
for i in range(nbit):
A[i, i] = 1
A[i, nbit] = pub[i]
A[nbit, nbit] = -c
res = A.LLL()
x= []
for i in range(len(res.rows())):
row = res.row(i).list()
is_binary = True
for m in row:
if m !=0 and m!=1:
is_binary=False
break
if is_binary:
print(i,row) #得到一组只有0和1的数组
flag=''.join(str(j)for j in row[:-1])
print(hex(int(flag,2)))
使用有理数域**QQ**来构造矩阵L
pubkey = []
c =
L = matrix(QQ,len(pubkey) + 1,len(pubkey) + 1)
# N = nextprime(iroot(len(pubkey),2)[0]//2)
for i in range(len(pubkey)):
L[i,i] = 1
L[i,len(pubkey)] = pubkey[i]
for i in range(len(pubkey)):
L[len(pubkey),i]=1/2
L[-1,-1] = c #(L[len(pubkey),len(pubkey)]=-c)
L = L.LLL()
#print(L)
for i in range(len(pubkey) + 1):
M = L.row(i).list()[:-1]
flag = True
for m in M:
if m != 1/2 and m != -1/2: # 否定则为m = 1/2 或 -1/2,故此处and是合理的
flag = False
break
if flag:
m = ''
print(i,M)
for j in M:
if j == -1/2: # 此处并不确定哪个代表二进制1
m = '1' + m # 上面分析时说过,得出的是从低位到高位,故后面得出的数放前面可得正确m
else:
m = '0' + m
print(hex(int(m,2)))
break


 浙公网安备 33010602011771号
浙公网安备 33010602011771号