三元LCG

题目:

from Crypto.Util.number import *
from secret import FLAG
p = getPrime(128)
step = len(FLAG) // 3
xs = [bytes_to_long(FLAG[:step]), bytes_to_long(FLAG[step:2*step]), bytes_to_long(FLAG[2*step:])]
a = getPrime(64)
b = getPrime(64)
c = getPrime(64)
a = 18038175596386287827
b = 15503291946093443851
c = 17270168560153510007
p = 307956849617421078439840909609638388517

for _ in range(10):
    new_state = (a*xs[0] + b*xs[1] + c*xs[2]) % p
    xs = xs[1:] + [new_state]
    #print(xs)
print(xs)
print(a, b, c, p)
[255290883651191064919890629542861653873,221128501895959214555166046983862519384,108104020183858879999084358722168548984]

解题思路:

• 通过<font style="color:rgb(6, 6, 7);">ani = MMI(a, n)</font>计算<font style="color:rgb(6, 6, 7);">a</font>在模 <font style="color:rgb(6, 6, 7);">n</font>下的逆元<font style="color:rgb(6, 6, 7);">a</font><sup><font style="color:rgb(6, 6, 7);">-1</font></sup>
• 然后逆元<font style="color:rgb(6, 6, 7);">a</font><sup><font style="color:rgb(6, 6, 7);">−1</font></sup>用于解线性同余方程
• 通过线性方程<font style="color:rgb(6, 6, 7);">seed=a</font><sup><font style="color:rgb(6, 6, 7);">−1</font></sup><font style="color:rgb(6, 6, 7);">⋅(seed−b) (mod n)</font>更新<font style="color:rgb(6, 6, 7);">seed</font>的值
• 每次更新后,将新的<font style="color:rgb(6, 6, 7);">seed</font>放入<font style="color:rgb(6, 6, 7);">xs</font>的第一个位置,同时保留前两个值(每次将新生成的xn替换到xs的第三位上,前两位分别是上一次的二三位;依次从x8,9,10还原7回退到7,8,9 以此类推推出初始xs)

解答:

from libnum import *

a = 18038175596386287827
b = 15503291946093443851
cc = 17270168560153510007
n = 307956849617421078439840909609638388517
xs = [255290883651191064919890629542861653873,221128501895959214555166046983862519384,108104020183858879999084358722168548984]

for i in range(10):
    #真实密文
    c = xs[2]
    #print(c)
    MMI = lambda A, n,s=1,t=0,N=0: (n<2 and t%N or MMI(n,A%n,t,s-A//n*t,N or n),-1)[n<1] #逆元计算
    ani = MMI(a,n)
    seed = c

    #计算出真实b
    b = 15503291946093443851
    b = b * xs[0] + cc * xs[1]

    seed = (ani * (seed - b)) % n
    print(seed)
    xs = [seed] + xs[0:2]
    print(xs)

    print(n2s(int(xs[0])))
    print(n2s(int(xs[1])))
    print(n2s(int(xs[2])))
    print("")

'''
b'flag{try_some'
b'_linear_algeb'
b'ra_technique}'
'''

ai一把梭

AI思路:

已知条件

1. 最后三个状态值：xs（代码输出的最后三个值）
2. 参数：a、b、c和p
3. 生成公式：new_state = (a*xs[0] + b*xs[1] + c*xs[2]) % p

解密思路

1. 逆向计算：从已知的最后三个状态值出发，利用生成公式逆向推导出前面的状态值
2. 恢复初始状态：通过逆向计算，逐步恢复出初始状态xs，即最初的三个值
3. 恢复**FLAG**：将恢复的初始状态值转换回字节序列，拼接起来得到原始的FLAG

具体步骤

1. 逆向计算公式

已知： new_state=(a⋅xs[0]+b⋅xs[1]+c⋅xs[2]) mod p

逆向计算公式：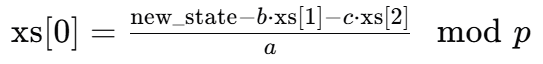

由于是在模 p 的情况下，需要计算模逆元： xs[0]=(new_state−b⋅xs[1]−c⋅xs[2])⋅a⁻¹ mod p

其中 a⁻¹ 是 a 在模 p 下的逆元，可以通过扩展欧几里得算法计算

2. 逆向计算状态值

从已知的最后三个状态值xs开始，逐步逆向计算前面的状态值

3. 恢复初始状态

逆向计算 10 次，恢复出最初的三个状态值

4. 转换为字节序列

将恢复的三个状态值转换为字节序列，拼接起来得到原始的FLAG

from Crypto.Util.number import long_to_bytes

# 已知参数
a = 18038175596386287827
b = 15503291946093443851
c = 17270168560153510007
p = 307956849617421078439840909609638388517

# 已知的最后三个状态值
xs = [255290883651191064919890629542861653873,221128501895959214555166046983862519384,108104020183858879999084358722168548984]

# 计算模逆元
def mod_inverse(x, p):
    return pow(x, -1, p)

# 逆向计算
a_inv = mod_inverse(a, p)
for _ in range(10):
    new_state = xs[-1]
    xs = xs[:-1]
    xs.insert(0, (new_state - b * xs[0] - c * xs[1]) * a_inv % p)

# 恢复初始状态
initial_states = xs

# 转换为字节序列
step = len(initial_states) // 3
flag_parts = [long_to_bytes(state) for state in initial_states]
flag = b''.join(flag_parts)

print("Recovered FLAG:", flag)
#flag{try_some_linear_algebra_technique}