LCG隔位输出(多次连续加密)

题目:

from Crypto.Util.number import *

flag = b'NSSCTF{******}'

class LCG:
    def __init__(self, seed, a, b, m):
        self.seed = seed  # 初始种子
        self.a = a  # 乘数
        self.b = b  # 增量
        self.m = m  # 模数

    def generate(self):
        self.seed = (self.a * self.seed + self.b) % self.m
        self.seed = (self.a * self.seed + self.b) % self.m
        return self.seed

lcg = LCG(bytes_to_long(flag), getPrime(255), getPrime(255), getPrime(256))

for i in range(getPrime(16)):
    lcg.generate()

print(lcg.generate())
print(lcg.generate())
print(lcg.generate())
print(lcg.generate())
print(lcg.generate())
'''
25445927935559969212648839062255651208014967526951331344342413906051118248013,
81572970970116732975667604095930675262596098540738447440566868976253289440293,
6956793925625110803779114150160476498676179542815207353218944386232051429289,
88042506866508011592456777776490262927213783361334741921985316105965255450508,
5652832125321707726481846809536180176877263519327268361130605456255558285092
'''

解题思路:

• 这里进行了两次加密,我们得到的并不是连续的输出,而是隔位输出,比如是 X2,X4,X6,X8,X10

def generate(self):
        self.seed = (self.a * self.seed + self.b) % self.m
        self.seed = (self.a * self.seed + self.b) % self.m
        return self.seed

• 首先要恢复模数m,依然可以构造消去增量b构造等比数列,所以我们依然可以用之前的方法求m

  

• 接下来就是求a

  

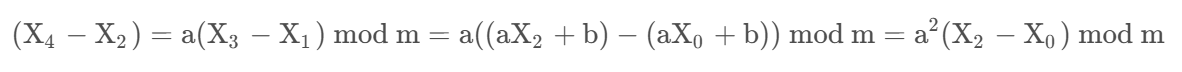
• 然后就是这个a^2,可以把a^2看作a,把(a+1)*b看成b,这样就相当于重新构造了一个LCG

解答:

import gmpy2
from Crypto.Util.number import GCD, isPrime, long_to_bytes

c = [25445927935559969212648839062255651208014967526951331344342413906051118248013,
81572970970116732975667604095930675262596098540738447440566868976253289440293,
6956793925625110803779114150160476498676179542815207353218944386232051429289,
88042506866508011592456777776490262927213783361334741921985316105965255450508,
5652832125321707726481846809536180176877263519327268361130605456255558285092]

t=[]
for i in range(1,len(c)):
    t.append(c[i]-c[i-1])

m = 0
for i in range(1,len(t)-1):
    m = GCD(t[i+1]*t[i-1]-t[i]**2, m)
# print(isPrime(m))   # true

a = (c[3]-c[2])*gmpy2.invert(c[2]-c[1],m) % m
b = (c[2]-a*c[1]) % m    # 把(a+1)*b当成b就可以了
# print(gmpy2.gcd(a,m))
# print(gmpy2.gcd(b,m))
a_1=gmpy2.invert(a,m)

for i in range(2**16):
    c[1] = (c[1]-b) * a_1 % m
    flag = long_to_bytes(c[1])

    if b'NSSCTF{' in flag:
        print(flag)
        break
#NSSCTF{step_step_step}