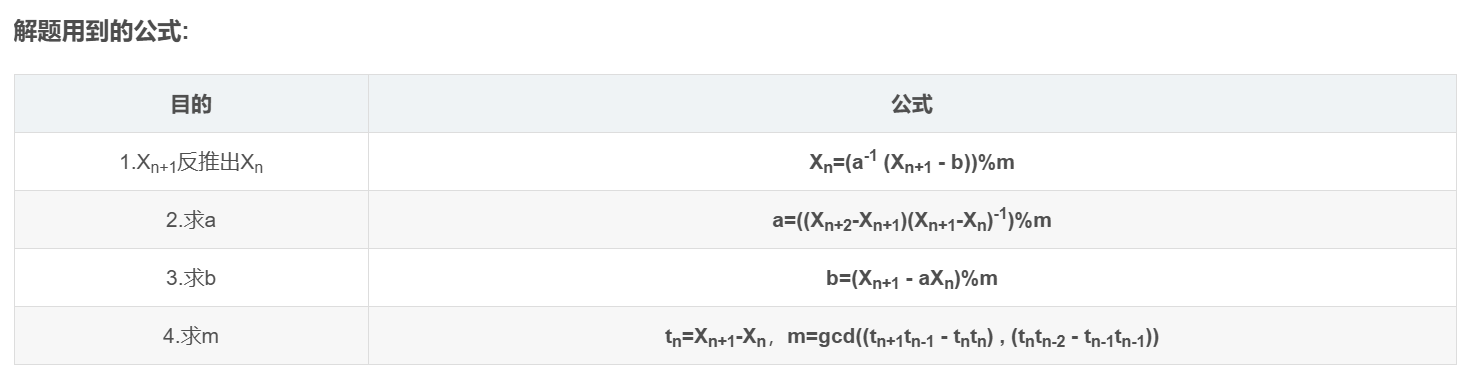
已知seed,a,b,n,c

知识拓展:

1.LCG的基本原理

LCG是一种基于线性同余关系的伪随机数生成器,它通过一个简单的递推公式生成一系列伪随机数,虽然这些数看起来是随机的,但实际上它们是通过确定性的算法生成的,因此称为"伪随机数"

2. LCG的递推公式

LCG的核心是一个递推公式,用于生成下一个伪随机数,公式如下: X_n+1=(aX_n+b) mod m 其中:

• X_n 是当前的随机数
• X_n+1 是下一个随机数
• X 表示生成的伪随机数序列,其中X₀是初始值,也被称为种子(seed)
• a 是乘数(Multiplier),必须是一个与m互素的正整数
• b 是增量(Increment),也必须是一个与m互素的正整数
• m 是模数(Modulus),必须一个大于0的正整数

题目:

from Crypto.Util.number import *
flag = b'Spirit{***********************}'

plaintext = bytes_to_long(flag)
length = plaintext.bit_length()

a = getPrime(length)
b = getPrime(length)
n = getPrime(length)

seed = 33477128523140105764301644224721378964069
print("seed = ",seed)
for i in range(10):
    seed = (a*seed+b)%n
ciphertext = seed^plaintext
print("a = ",a)
print("b = ",b)
print("n = ",n)
print("c = ",ciphertext)
# seed =  33477128523140105764301644224721378964069
# a =  216636540518719887613942270143367229109002078444183475587474655399326769391
# b =  186914533399403414430047931765983818420963789311681346652500920904075344361
# n =  155908129777160236018105193822448288416284495517789603884888599242193844951
# c =  209481865531297761516458182436122824479565806914713408748457524641378381493

解题思路:

• 想要得到flag就要知道plaintext
• 想要知道plaintext只能通过ciphertext = seed ^ plaintex这个表达式推出
• 而ciphertext==c我们知道,式子中的seed可以通过他给的初始seed,a,b,n运用算法lcg十次得到
• 然后根据异或的特性求解出plaintext,即plaintext = seed ^ ciphertext

(异或特性,c=a异或b,那么a=b异或c,或者b=a异或c)

解答:

from Crypto.Util.number import *

seed = 33477128523140105764301644224721378964069
a = 216636540518719887613942270143367229109002078444183475587474655399326769391
b = 186914533399403414430047931765983818420963789311681346652500920904075344361
n = 155908129777160236018105193822448288416284495517789603884888599242193844951
c = 209481865531297761516458182436122824479565806914713408748457524641378381493
for i in range(10):
    seed = (a * seed + b) % n

m = c ^ seed
print(long_to_bytes(m))
#Spirit{0ops!___you_know__LCG!!}