已知m高位攻击

题目:

from Crypto.Util.number import *

p = getPrime(512)
q = getPrime(512)

flag = b'NSSCTF{******}'

n = p*q
m = bytes_to_long(flag)

e = 3
c = pow(m, e, n)

print(f'n = {n}')
print(f'm = {m>>100}')
print(f'c = {c}')

'''
n = 1527542955109141740955682973826193262775892499957309448026045241470857728195657663426381459817190647872750820593934305392986732687654051540838628636529717414135863605586498459487983117670942529496973140251670874510207985224170313618738268651184582186637089407746738836054395760157095709388670653150429457223183161697730087281761369404956762102465246289770300941300936135728738323821631682286737786472020790680432476428922187234364341215016265407571963282147129157
m = 2214226572250613833249705195927505959981823363137633354626532745196588970707
c = 22113876206623661468496987580282614626160320529328454393375952035910523390370709980915981609422504775420007441257006956611997263223244837790238493516238723139514158563675396731542096229586616735753203254810465452822757959264870210654015436735165961713016222816604825816304606749448517022584926571828009062411578367333
'''

解题思路:

• 本题泄露了m的高位
• 那么这些泄露的数据有什么用呢,我们考虑RSA的加密本质实际上就是一个模多项式

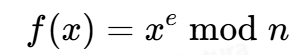
• 现在我们得到了其中的一个函数值即f(m)=c,所以等于我们要求解模多项式的根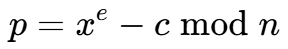

    ![](https://cdn.nlark.com/yuque/0/2025/png/49294098/1739696057262-5bdafa75-d606-47ee-ac37-8eb5667561ac.png)
  

• Coppersmith可以求解小根,但是这这里的<font style="color:rgb(0, 0, 0);">m</font>还是太大了,但是因为<font style="color:rgb(0, 0, 0);">m</font>的高位泄露了,我们可以将<font style="color:rgb(0, 0, 0);">m</font>写为

<font style="color:rgb(0, 0, 0);">m=m</font><sub><font style="color:rgb(0, 0, 0);">h</font></sub><font style="color:rgb(0, 0, 0);">+x</font>,此时有:

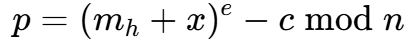
• 此时我们还知道<font style="color:rgb(0, 0, 0);">x</font>位数为100,显然小于<font style="color:rgb(0, 0, 0);">n</font><sup><font style="color:rgb(0, 0, 0);">1/e</font></sup>(1024/3位);所以我们便可以用Coppersmith进行求解根

解答:

from gmpy2 import *
from Crypto.Util.number import *

n = 1527542955109141740955682973826193262775892499957309448026045241470857728195657663426381459817190647872750820593934305392986732687654051540838628636529717414135863605586498459487983117670942529496973140251670874510207985224170313618738268651184582186637089407746738836054395760157095709388670653150429457223183161697730087281761369404956762102465246289770300941300936135728738323821631682286737786472020790680432476428922187234364341215016265407571963282147129157
m = 2214226572250613833249705195927505959981823363137633354626532745196588970707
c = 22113876206623661468496987580282614626160320529328454393375952035910523390370709980915981609422504775420007441257006956611997263223244837790238493516238723139514158563675396731542096229586616735753203254810465452822757959264870210654015436735165961713016222816604825816304606749448517022584926571828009062411578367333

m = m<<100

print(m)
#2806865643354785581450142994351107732326351637470254633277360198619644201710864636143835565518735468920832
PR.<x> = PolynomialRing(Zmod(n))

f = (m+x)^3 - c
res = f.small_roots()
m = int(res[0] + m)
print(m)
#2806865643354785581450142994351107732326351637470254633277360198619644201711450860255199207594318928228477
print(bytes.fromhex(hex(m)[2:]))
#NSSCTF{688404a6-c408-4196-bc43-7f18317a9170}