短填充攻击

题目:

from Crypto.Util.number import *
m = bytes_to_long(b'NSSCTF{******}')

p = getPrime(512)
q = getPrime(512)

n = p*q

e = 9

r = getPrime(512)

c1 = pow(m, e, n)
c2 = pow(m+r, e, n)

print(f'c1 = {c1}')
print(f'c2 = {c2}')
print(f'r = {r}')
print(f'n = {n}')

'''
c1 = 135074766579407676786282087896424573055829820741326911395660008092908906818293714163243721440579480398437184153110701014575949020137195005556115765711856362529093323957313305701439430406396620730435232669024347062255561124227077117736226705746520202121773331267896121082546807985584499775544186860738299210902
c2 = 52198561898892210533988782934627447441579509170862004216826284305082884787397969852570583444422705227177306845788090962326207704949679636373972262848806083888114511515323970306654941921527306928423850775839578728701294521014874290792581635297504014585143468088934951952990888189000603302912352199468290961647
r = 7226418134082605571805056000800553195029496658257912353583130240746954757224748488491991266548553899116384605868480860827154816241193159482670000874841821
n = 144690523587663809780722437199578577582544144694543134253077982812595463236242062416509866333774784681011350541203308061301675822157859373788530465702809816586981803008466959154241234879285863437666243631170277595720205934928759253610014553402523757331771549475265418644503305010214366648156173843801360148229
'''

解题思路:

当给出两组密文,且明文满足m2=m1+r时则可以使用该方式

(其实这就是线性填充广播攻击当a=1的情况)

• 可以直接用线性填充广播攻击的思路求解,不过这里我们如果不知道r该怎么求解呢

• 考虑两个二元多项式

  

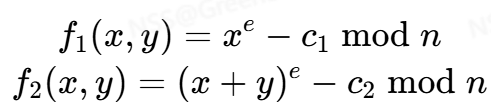
• 显然<font style="color:rgb(0, 0, 0);">(m1,r)</font>是多项式的一组根,而这里指出了这俩多项式经过<font style="color:rgb(0, 0, 0);">resultant</font>后将得到一个<font style="color:rgb(0, 0, 0);">y</font>的多项式,并且<font style="color:rgb(0, 0, 0);">r</font>是其中的一个根,则我们再利用CopperSmith求出这个小根即可得到<font style="color:rgb(0, 0, 0);">r</font>

解答:

def franklinReiter(n,e,r,c1,c2):
    R.<X> = Zmod(n)[]
    f1 = X^e - c1
    f2 = (X + r)^e - c2
    return Integer(n-(compositeModulusGCD(f1,f2)).coefficients()[0])

def compositeModulusGCD(a, b):
    if(b == 0):
        return a.monic()
    else:
        return compositeModulusGCD(b, a % b)

def CoppersmithShortPadAttack(e,n,C1,C2,eps=1/30):
    """
    求解r
    Figured out from: https://en.wikipedia.org/wiki/Coppersmith's_attack#Coppersmith.E2.80.99s_short-pad_attack
    """
    P.<x,y> = PolynomialRing(ZZ)
    ZmodN = Zmod(n)
    g1 = x^e - C1
    g2 = (x+y)^e - C2
    res = g1.resultant(g2)
    P.<y> = PolynomialRing(ZmodN)
    rres = 0
    # 这一步的目的是因为虽然res只包含y，但它还是在二元多项式环空间中，我们提取系数和指数重新生成一个一元多项式
    for i in range(len(res.coefficients())):
        rres += res.coefficients()[i]*(y^(res.exponents()[i][1]))

    diff = rres.small_roots(epsilon=eps)
    return int(diff[0])

c1 = 135074766579407676786282087896424573055829820741326911395660008092908906818293714163243721440579480398437184153110701014575949020137195005556115765711856362529093323957313305701439430406396620730435232669024347062255561124227077117736226705746520202121773331267896121082546807985584499775544186860738299210902
c2 = 52198561898892210533988782934627447441579509170862004216826284305082884787397969852570583444422705227177306845788090962326207704949679636373972262848806083888114511515323970306654941921527306928423850775839578728701294521014874290792581635297504014585143468088934951952990888189000603302912352199468290961647
r = 7226418134082605571805056000800553195029496658257912353583130240746954757224748488491991266548553899116384605868480860827154816241193159482670000874841821
n = 144690523587663809780722437199578577582544144694543134253077982812595463236242062416509866333774784681011350541203308061301675822157859373788530465702809816586981803008466959154241234879285863437666243631170277595720205934928759253610014553402523757331771549475265418644503305010214366648156173843801360148229

m = franklinReiter(n, 9, r, c1, c2)
print(hex(m))
print(bytes.fromhex(hex(m)[2:]))
#0x4e53534354467b35333962376330372d666265392d343165392d626163612d3035393130323063613638337d
#NSSCTF{539b7c07-fbe9-41e9-baca-0591020ca683}