Schemidt-Samoa密码

题目:

from Crypto.Util.number import *
flag = b'NSSCTF{******}'

p = getPrime(512)
q = getPrime(512)
n = p*p*q
e = n

c = pow(bytes_to_long(flag), e, n)
d = inverse(e, (p-1)*(q-1))

print(f'n = {n}')
print(f'd = {d}')
print(f'c = {c}')

'''
n = 539403894871945779827202174061302970341082455928364137444962844359039924160163196863639732747261316352083923762760392277536591121706270680734175544093484423564223679628430671167864783270170316881238613070741410367403388936640139281272357761773388084534717028640788227350254140821128908338938211038299089224967666902522698905762169859839320277939509727532793553875254243396522340305880944219886874086251872580220405893975158782585205038779055706441633392356197489
d = 58169755386408729394668831947856757060407423126014928705447058468355548861569452522734305188388017764321018770435192767746145932739423507387500606563617116764196418533748380893094448060562081543927295828007016873588530479985728135015510171217414380395169021607415979109815455365309760152218352878885075237009
c = 192900246089028524753714085947506209686933390275949638288635203069117504901164350538204619142802436833736532680210208373707687461486601253665313637541968852691434282584934523173439632554783111037594035333325446559685553119339191110056283203940511701992217372405369575376549738295022767068810511670144120539082403063406787770958515441813335548550876818218065412869322721395317537328975187612606437225577060414403223288106406471061759010085578263501971809720648827
'''

解题思路:

• 和以往的RSA稍有不同,这里的

n=p²q

e=n

• 同时我们直接得到了d,按照RSA的思路则直接c^d mod n即可,但是我们会发现解密出来是乱码,说明这样解密是不对的,实际上这是一种名为Schemidt-Samoa的非对称密码,而它的解密方式为

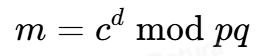
解答:

from gmpy2 import *
from Crypto.Util.number import *

def getPQ(pub, priv):
    return gmpy2.gcd(pub, gmpy2.powmod(2, pub*priv, pub)-2)


def decrypt(pub, priv, enc):
    return gmpy2.powmod(enc, priv, getPQ(pub, priv))

n = 539403894871945779827202174061302970341082455928364137444962844359039924160163196863639732747261316352083923762760392277536591121706270680734175544093484423564223679628430671167864783270170316881238613070741410367403388936640139281272357761773388084534717028640788227350254140821128908338938211038299089224967666902522698905762169859839320277939509727532793553875254243396522340305880944219886874086251872580220405893975158782585205038779055706441633392356197489
d = 58169755386408729394668831947856757060407423126014928705447058468355548861569452522734305188388017764321018770435192767746145932739423507387500606563617116764196418533748380893094448060562081543927295828007016873588530479985728135015510171217414380395169021607415979109815455365309760152218352878885075237009
c = 192900246089028524753714085947506209686933390275949638288635203069117504901164350538204619142802436833736532680210208373707687461486601253665313637541968852691434282584934523173439632554783111037594035333325446559685553119339191110056283203940511701992217372405369575376549738295022767068810511670144120539082403063406787770958515441813335548550876818218065412869322721395317537328975187612606437225577060414403223288106406471061759010085578263501971809720648827


pq = getPQ(n, d)
m = decrypt(n, d, c)
print(long_to_bytes(m))
#NSSCTF{864098e7-7ef1-4c7e-90d6-d103d8c272e0}