中国剩余定理(CRT)的运用
题目:
from Crypto.Util.number import *
from secret import flag
flag=bytes_to_long(flag)
l=flag.bit_length()//3 + 1
n=[]
N=1
while len(n) < 3:
p = 4*getPrime(l)-1
if isPrime(p):
n.append(p)
N *= p
print(f'c={flag*flag%N}')
from sympy import symbols, expand
x = symbols('x')
polynomial = expand((x - n[0]) * (x - n[1]) * (x - n[2]))
print(f'{polynomial=}')
# c=24884251313604275189259571459005374365204772270250725590014651519125317134307160341658199551661333326703566996431067426138627332156507267671028553934664652787411834581708944
# polynomial=x**3 - 15264966144147258587171776703005926730518438603688487721465*x**2 + 76513250180666948190254989703768338299723386154619468700730085586057638716434556720233473454400881002065319569292923*x - 125440939526343949494022113552414275560444252378483072729156599143746741258532431664938677330319449789665352104352620658550544887807433866999963624320909981994018431526620619
解题思路:
密文生成:
<font style="color:rgb(6, 6, 7);">l</font>是每个质数的位数,通过flag.bit_length() // 3 + 1计算得到- 生成了三个特殊的质数
n[0],n[1]和n[2],每个质数的形式为<font style="color:rgb(6, 6, 7);">p=4×getPrime(l)−1</font>,并且确保p也是质数 - 计算模数
<font style="color:rgb(6, 6, 7);">N=n[0]*n[1]*n[2]</font> - 密文
<font style="color:rgb(6, 6, 7);">c</font>通过<font style="color:rgb(6, 6, 7);">c=flag^2 mod N</font>生成
多项式生成:
- 使用
sympy库生成了一个三次多项式,其根为<font style="color:rgb(6, 6, 7);">n[0]</font>,<font style="color:rgb(6, 6, 7);">n[1]</font>和<font style="color:rgb(6, 6, 7);">n[2]</font>:<font style="color:rgb(6, 6, 7);">polynomial=(x−n[0])*(x−n[1])*(x−n[2])</font> - 展开后的多项式形式为:
<font style="color:rgb(6, 6, 7);">polynomial=x^3−(n[0]+n[1]+n[2])x^2+(n[0]n[1]+n[1]n[2]+n[2]n[0])x−n[0]n[1]n[2]</font>
解答:
- 首先求得多项式的根
- 通常
c是根据m^e mod N生成,因此我们这里假定e=2 - 再运用有限域的开方求解一个模质数
n[i]意义下的方程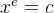 的解
的解 - 最后利用中国剩余定理(CRT)去遍历所有的解
解答:
法1:有限域的开方+CRT
- 求方程的根
# 定义变量
x = var('x')
# 已知的多项式字符串
polynomial_str = "x**3 - 15264966144147258587171776703005926730518438603688487721465*x**2 + 76513250180666948190254989703768338299723386154619468700730085586057638716434556720233473454400881002065319569292923*x - 125440939526343949494022113552414275560444252378483072729156599143746741258532431664938677330319449789665352104352620658550544887807433866999963624320909981994018431526620619"
# 将字符串转换为Sage表达式
polynomial = sage_eval(polynomial_str, locals={'x': x})
# 求解多项式方程
roots = solve(polynomial == 0, x)
# 输出根
print("The roots of the polynomial are:")
for root in roots:
print(root)
'''
The roots of the polynomial are:
x == 5487564316951417093934647798659941512646442958127439071827
x == 5908636118089697338533572785710162817248001570348495067227
x == 3868765709106144154703556118635822400623994075212553582411
'''
- 求解一个模质数n[i]意义下的方程
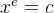 的解
的解
c = 24884251313604275189259571459005374365204772270250725590014651519125317134307160341658199551661333326703566996431067426138627332156507267671028553934664652787411834581708944
e = 2
n = 125440939526343949494022113552414275560444252378483072729156599143746741258532431664938677330319449789665352104352620658550544887807433866999963624320909981994018431526620619
p = 5487564316951417093934647798659941512646442958127439071827
q = 5908636118089697338533572785710162817248001570348495067227
r = 3868765709106144154703556118635822400623994075212553582411
R = Zmod(p)['x']; (x,) = R._first_ngens(1)
f = x ** e - c
f = f.monic()
res1 = f.roots()
print('res1 = ',res1)
R = Zmod(q)['x']; (x,) = R._first_ngens(1)
f = x ** e - c
f = f.monic()
res2 = f.roots()
print('res2 = ',res2)
R = Zmod(r)['x']; (x,) = R._first_ngens(1)
f = x ** e - c
f = f.monic()
res3 = f.roots()
print('res3 = ',res3)
'''
res1 = [(5212735863395943288910959852640920033190508878765872629842, 1), (274828453555473805023687946019021479455934079361566441985, 1)]
res2 = [(4725223583123785863404548749849456718900150991615252259928, 1), (1183412534965911475129024035860706098347850578733242807299, 1)]
res3 = [(3246915958185332968953452707900267984480404202681728477174, 1), (621849750920811185750103410735554416143589872530825105237, 1)]
'''
- 利用中国剩余定理CRT去遍历所有的解
from Crypto.Util.number import long_to_bytes
import libnum
n0 = 5487564316951417093934647798659941512646442958127439071827
n1 = 5908636118089697338533572785710162817248001570348495067227
n2 = 3868765709106144154703556118635822400623994075212553582411
res1 = [(5212735863395943288910959852640920033190508878765872629842, 1), (274828453555473805023687946019021479455934079361566441985, 1)]
res2 = [(4725223583123785863404548749849456718900150991615252259928, 1), (1183412534965911475129024035860706098347850578733242807299, 1)]
res3 = [(3246915958185332968953452707900267984480404202681728477174, 1), (621849750920811185750103410735554416143589872530825105237, 1)]
for i in res1:
for j in res2:
for k in res3:
m = libnum.solve_crt([int(i[0]),int(j[0]),int(k[0])],[n0,n1,n2])
flag = long_to_bytes(m)
if b'VNCTF{' in flag:
print(flag)
#VNCTF{90dcfb2dfb21a21e0c8715cbf3643f4a47d3e2e4b3f7b7975954e6d9701d9648}
法2:rabin算法
from sympy import symbols, Eq, solve
from Crypto.Util.number import *
import itertools
x = symbols('x')
c = 24884251313604275189259571459005374365204772270250725590014651519125317134307160341658199551661333326703566996431067426138627332156507267671028553934664652787411834581708944
polynomial = x**3 - 15264966144147258587171776703005926730518438603688487721465*x**2 + 76513250180666948190254989703768338299723386154619468700730085586057638716434556720233473454400881002065319569292923*x - 125440939526343949494022113552414275560444252378483072729156599143746741258532431664938677330319449789665352104352620658550544887807433866999963624320909981994018431526620619
n = solve(Eq(polynomial, 0), x)
N = 1
for p in n:
N *= p
def crt(primes, remainders):
result = 0
for i in range(len(primes)):
Mi = N // primes[i]
inv = inverse(Mi, primes[i])
result += remainders[i] * Mi * inv
return result % N
roots = [pow(c, (int(p) + 1) // 4, int(p)) for p in n]
# 遍历所有可能的符号组合
for signs in itertools.product([1, -1], repeat=3):
adjusted_roots = [
signs[0] * roots[0] % n[0],
signs[1] * roots[1] % n[1],
signs[2] * roots[2] % n[2]
]
flag = crt(n, adjusted_roots)
print(long_to_bytes(flag))
'''
b"9\xb3\x11\x03*o\xd4v\xbcU@\x14R\xd4\xa5\xf1'nX\xe0V\x0e\x98\x92\x05\x19\x0750\x19\xdc\x8d\xb9\xee\xc9\x90\x00\xe9\xa4\xab:\xc6qh5`\x83G\x80@\n\xf6`\x0b|#\xd9\x90,\xb1\x07\xa5\xcba\x81\xb1\x19f\xcb\xd2\xb8\xc6"
b'>PO\x0eF\x7f\\$\xf8\x9e!\xf6\x05\x11\x0c\xd5v\x0cY\xa3\xe4\xbf\xf4\xe8|y \xa2\xeet\x0bm\\\xf7\x0cX\x80<\x1d\xd06\x9b0\xf5%\x16\xc0\xb6v\x96)\n\xde\x1a\xc5!\xfa%\x11$\xe6h\x84\xc1\xb4\xda\x01\x11\xb5kFS'
b'}\x8f\x96I\xdf\xd5j\xfa\xff\xe2N\x02\x9a@\x90vO\xef\xe9\xa7<7\xb72\xa5\xeb6\x88\x19\xbcs\xec\xb2H\xd4\xe1_\x8b\xab\xfd\xdc\x9b:\n\xad\x15\xa3m\xd1k\xceb\x00\xb3\x06P\x99\xf1\x93\xc6z/\x888\x9dI\x91h\xf4Ex\xbb'
b'VNCTF{90dcfb2dfb21a21e0c8715cbf3643f4a47d3e2e4b3f7b7975954e6d9701d9648}'
b'\x81\x807\xceSW\xfc6\xdbbi\x17\x88\x18.\x8d\xda)\x87\xa8f\x86I(V\xda\xe1\x93mO\xdd\xff\xee\xe4\xafC\x12ub\xbai\xa7\x92\xcd8\x01x\x18`\xf5}\xb2\x10O\xe0\xe4H\x1c\x0fo\xec)\xcf*p\x0f\xb0\xa1qu\x95N'
b"\x04F\xef\xc7\xc7\xc9\x0cu\x0b\xe4~{P\n\x02}\xeck\xcfb\\\x7f\xf7&\x14'\xe2<\x88\xf6\xccyo\xd2\x0e\x95\x19\x1e\x17\xf0\xc4p\x8c'\xbdQ\t\x0c\xc2\xef\xe6\xb2F\xd6\x11\xc8\xe7_\xb0\x0e\xa8^\x80)\x02\xf7\x83q\xb3dU\x10"
b'C\x867\x03a\x1f\x1bK\x13(\xaa\x87\xe59\x86\x1e\xc6O_e\xb3\xf7\xb9p=\x99\xf8!\xb4?4\xf8\xc5#\xd7\x1d\xf8m\xa6\x1ejp\x95=EO\xeb\xc4\x1d\xc5\x8c\tinR\xf7\x87,2\xb0<%\x83\x9f\xebg\x13\xc8\xf2>\x87x'
b'H#u\x0e}.\xa2\xf9Oq\x8ci\x97u\xed\x03\x14\xed`)B\xa9\x15\xc6\xb4\xfa\x11\x8fr\x99c\xd8h,\x19\xe6w\xc0\x1fCfET\xca5\x06)3\x14\x1b\xaa\x1d\xe7}\x9b\xf5\xa7\xc1\x17$\x1a\xe8=\x00\x1e\x8f\xfbs\xdb\xd7\x15\x05'
'''


 浙公网安备 33010602011771号
浙公网安备 33010602011771号