差值分解素因数(m大于n)

题目:

from Crypto.Util.number import *
import gmpy2
FLAG = b'flag{                               '
m = bytes_to_long(FLAG)
p =    #  a prime
q =    #  a prime
n = p*q
e = 65537
c = pow(m,e,n)
print('n=',n)
print('c=',c)
'''
n=16026690428477930599319309987814117360807203959333979485460616887444993030960723667744637313561710383341307655954326470212089349757841149802435975533
c=3578657998616757595773234766900753933819276902828912201780063132276893321988014757347257217896296660797699342180321599128083290554436351526909362708
'''

解题思路:

因为RSA加密的同余性质可能导致解密结果不是原始明文,而是一个偏移量。循环检查从2**20(即1,048,576)个可能的偏移量

解答:

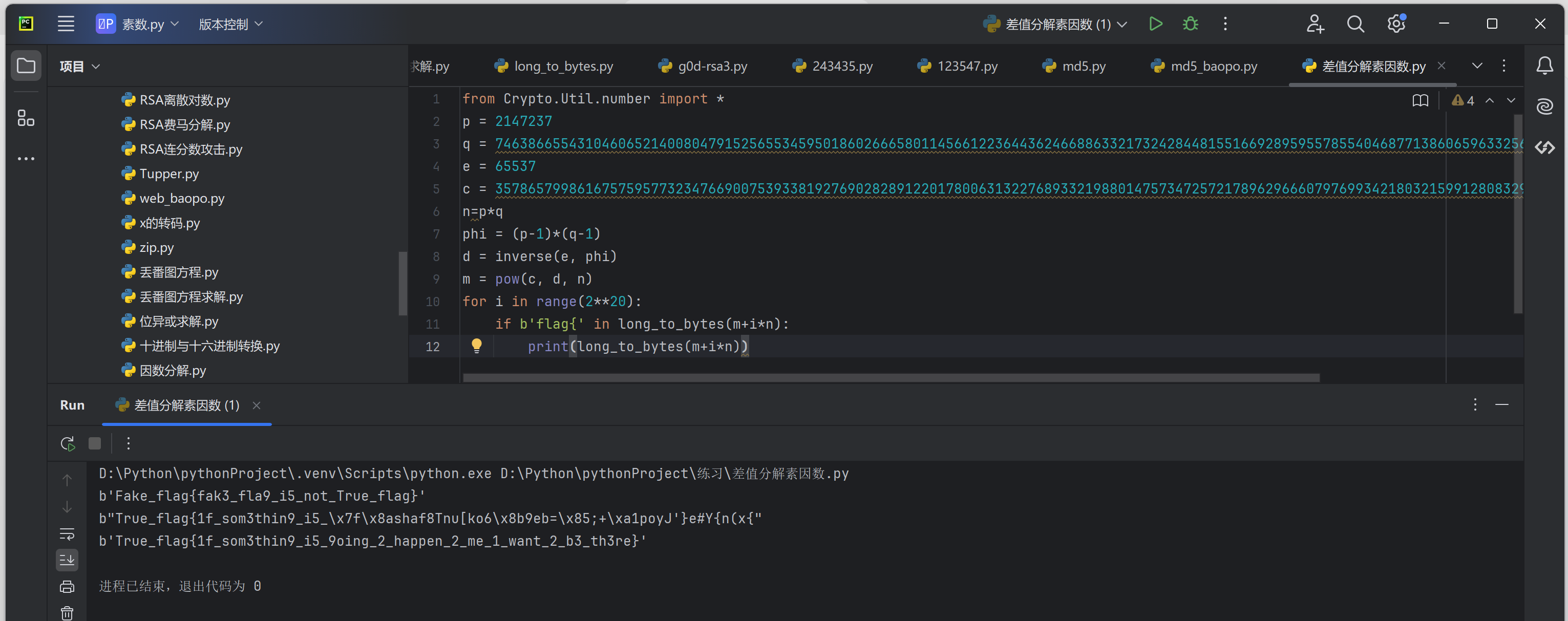
from Crypto.Util.number import *
p = 2147237
q = 7463866554310460652140080479152565534595018602666580114566122364436246688633217324284481551669289595578554046877138606596332565877842618119209
e = 65537
c = 3578657998616757595773234766900753933819276902828912201780063132276893321988014757347257217896296660797699342180321599128083290554436351526909362708
n=p*q
phi = (p-1)*(q-1)
d = inverse(e, phi)
m = pow(c, d, n)
for i in range(2**20):
    if b'flag{' in long_to_bytes(m+i*n):
        print(long_to_bytes(m+i*n))

'''
b'Fake_flag{fak3_fla9_i5_not_True_flag}'
b"True_flag{1f_som3thin9_i5_\x7f\x8ashaf8Tnu[ko6\x8b9eb=\x85;+\xa1poyJ'}e#Y{n(x{"
b'True_flag{1f_som3thin9_i5_9oing_2_happen_2_me_1_want_2_b3_th3re}'
'''

最后我们发现n真的小于m2,而m1小于n

from Crypto.Util.number import *
m1 = b'Fake_flag{fak3_fla9_i5_not_True_flag}'
m2 = b'True_flag{1f_som3thin9_i5_9oing_2_happen_2_me_1_want_2_b3_th3re}'
m1 = bytes_to_long(m1)
m2 = bytes_to_long(m2)
print(m1)
print(m2)
#m1=35001880411086343343343898392484061141996750808533271876755483488463443257632336554059645
#m2=4422853704166197551632951338717086339827242462249479650643595521229421717179255332483495968541482152211930742006936839208245357162435349686310987849950589
#n =16026690428477930599319309987814117360807203959333979485460616887444993030960723667744637313561710383341307655954326470212089349757841149802435975533