2025-11-07

数论

1.P6583 回首过去 - 洛谷（十进制有限小数）

整数分块
因为直接计算O(n)

       for (int i = 1 ; i <= n ; ++ i){
           int j = i, o ;
           while (j % 2 == 0) j /= 2 ;
           while (j % 5 == 0) j /= 5 ;
           ans += n / j ;
       }

因此考虑使用整数分块优化
枚举l，找右端点r，所以在l~r中，n/l是恒定值
右端点求法r=n/(n/l)

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int mod = 998244353;
const int N=2e5+10;
int ans;

int sum(int x){//容斥
    return (x - x / 5 - x / 2 + x / 10);
}

//O((logn)^2)
int all_2_5(int x){//计算小于 x的 2^(re2)*5^(re5)总个数
    int res = 0;
    int re2 = log(x) / log(2) + 1;//算log2(x),即最大上标
    int re5 = log(x) / log(5) + 1;
    int sum2 = 1, sum5;
    for (int i = 0; i <= re2;i++){
        sum5 = 1;
        for (int j = 0; j <= re5;j++){
            if(sum5*sum2>x)
                break;
            sum5 = 5LL * sum5;
            res++;
        }
        sum2 *= 2LL;
    }
    return res;
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin >> n;
    for (int l = 1, r; l <= n;l=r+1){//整数分块操作
        r = n / (n / l);
        ans += (sum(r) - sum(l - 1)) * (n / l) * all_2_5(n / l);
    }
    cout << ans << endl;
}

2.P4139 上帝与集合的正确用法 - 洛谷(拓展欧几里得)（递归）

拓展欧几里得

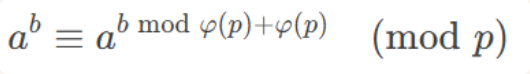
[!warning] 注意
快速幂用int时要防止整数溢出！！！

#include <bits/stdc++.h>
using namespace std;
#define LL long long
const LL mod = 998244353;
const int N = 1e7 + 10;
int p[N], vis[N], cnt;
int phi[N];

void get_phi(int n){
    phi[1] = 1;
    for (int i = 2; i <= n;i++){
        if(!vis[i]){
            p[cnt++] = i;
            phi[i] = i - 1;
        }
        for (int j = 0; p[j] <= n / i;j++){
            int m = i * p[j];
            vis[m] = 1;
            if(i%p[j]==0){
                phi[m] = p[j] * phi[i];
                break;//
            }else{
                phi[m] = (p[j] - 1) * phi[i];
            }
        }
    }
}

int qmi(int a,int b,int p)
{
    int res=1;
    while(b)
    {
        if(b&1)
            res = 1LL*res * a % p;
        a=1LL*a*a%p;
        b >>= 1;
    }
    return res;
}

int solve(int p){//拓展欧拉函数，递归求解,O(logp)
    if(p==1)
        return 0;
    return qmi(2, solve(phi[p]) + phi[p], p);
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    get_phi(1e7);
    int T;
    cin >> T;
    while(T--){
        int p;
        cin >> p;
        cout << solve(p) << endl;
    }
}       

3.CF582A GCD Table - 洛谷(GCD)（CF1700）

找\(n^2\) 中最大num[i]
删去本身的数量，即mp[gcd(num[i],num[i])]
把num[i]与在a数组中所有gcd数量删去
gcd(num[i],a[j])，gcd(a[j],num[i])

#include <bits/stdc++.h>
using namespace std;
#define LL long long
const LL mod = 998244353;
const int N=250010;
int num[N], a[510];
int ans, cnt;
map<int, int> mp;
LL gcd(LL a,LL b){
    return b?gcd(b,a%b):a;
}
LL lcm(LL a,LL b){
    return a/gcd(a,b)*b;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin >> n;
    for (int i = 1; i <= n * n;i++){//O(n^2logn)
        int x;
        cin >> x;
        if(!mp[x])
            num[++cnt] = x;
        mp[x]++;
    }
    sort(num + 1, num + cnt + 1);
    for (int i = cnt; i >= 1 && ans < n;){
        while(!mp[num[i]])
            i--;
        a[++ans] = num[i];
        mp[num[i]]--;
        for (int j = 1; j < ans;j++){//O(n^2logn)
            mp[gcd(num[i], a[j])] -= 2;
        }
    }
    for (int i = 1; i <= ans;i++){
        cout << a[i] << " ";
    }
}

4.CF687B Remainders Game - 洛谷（1800）（拓展中国剩余定理）

还不会EXCRT...
有空的时候去学！！！

#include <bits/stdc++.h>
using namespace std;
#define LL long long
const LL mod = 998244353;
const int N=2e5+10;
LL gcd(LL a,LL b){
    return b?gcd(b,a%b):a;
}
LL lcm(LL a,LL b){
    return a/gcd(a,b)*b;
}
int p = 1;

//本题只要判断所有c的最小公倍数是否是 k的倍数
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    LL n, k;
    cin >> n >> k;
    for (int i = 1; i <= n;i++){
        LL c;
        cin >> c;
        p = (lcm(p, c)) % k;
    }
    if(p%k==0)
        cout << "Yes\n";
    else{
        cout << "No\n";
    }
}

又把LL忘了！！！

CF

Problem - 1516B - Codeforces（XOR）（1500）

暴力找解，因为找的是相邻元素

#include <bits/stdc++.h>
using namespace std;
#define LL long long
const LL mod = 998244353;
const int N=2010;
int a[N];

void solve()
{
    int n;
    cin >> n;
    int ans = 0;
    for (int i = 0; i < n;i++){
        cin >> a[i];
        ans ^= a[i];
    }
    if(ans==0){
        cout << "YES\n";
        return;
    }
    int now = 0, res = 0;
    for (int i = 0; i < n;i++){
        now ^= a[i];
        if(now==ans){
            res++;
            now = 0;
        }
    }
    if(res>2){
        cout << "YES\n";
    }else{
        cout << "NO\n";
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int T;
    cin >> T;
    while (T--)
    {
        solve();
    }
}

Problem - 1646C - Codeforces(状态压缩)

在n=\(10^{12}\) 范围，要会推最大阶乘为 15! ≈ 1.3×10¹²
计算所有阶乘和的可能，在加上剩余数关于2的幂的次数和

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int mod = 998244353;
const int N=2e5+10;
int f[20];
// 15! ≈ 1.3×10¹²
int getnum(int x){
    int res = 0;
    while(x){
        if(x&1)
            res++;
        x /= 2;
    }
    return res;
}

void solve()
{
    int n;
    cin >> n;
    int ans = 100;
    for (int i = 0; i < (1 << 13);i++){//状态压缩
        int t = 0, sum = 0;
        for (int j = 0; j < 13;j++){
            if(i>>j&1){
                t++;
                sum += f[j];
            }
        }
        if(n>=sum){
            ans = min(ans, t + getnum(n - sum));
        }
    }
    cout << ans << endl;
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int T;
    f[0] = 6;
    for (int i = 4; i <= 15;i++){
        f[i - 3] = f[i - 4] * i;
    }
    cin >> T;
    while (T--)
    {
        solve();
    }
}

碎碎念

早上就刷这些了，终于把洛谷数论题单刷完了，但是好像好多定理都忘的差不多了，大概周天的时候把整个进阶数论全部整理一遍！！！
下午吃朱富贵，晚上可能预习点离散数学