Arbitrage实验

一、     实验内容及目的

实验内容：

根据题目Arbitrage，用Floyd算法解出题目，并进行算法分析、效率分析、实验结果分析。

实验目的：

通过题目，深入理解Floyd算法的思想，体会Floyd算法的优缺点，了解更多的最短路算法。

分析的指标：

在相同数据规模的情况下的算法代码运行时间。以及通过数学方法计算出的时间复杂度。

二、实验方案

实验环境：Windows10 + Dev-C++ + 硬盘大小100GB + 8核处理器 + 16GB内存

题目描述：

 

将关键信息挑选出来，此题目可描述成：

题目首先给出N种货币，然后给出了这N种货币之间的兑换的兑换率。问在这N种货币中是否有货币可以经过若干次兑换后，兑换成原来的货币可以使货币量增加。

解题方案：

将每个可以兑换的货币之间想象为一个边，而边与边之间的权值就是这两个货币的兑换率，整个可以兑换的货币之间可以产生一个有向图。我们的目的是判断是否能够找到一条路径，从一个顶点出发再回到这个顶点的最长路径。存在这个最长路径也就意味着这个存在套汇的可能性。

首先把每个货币的单词映射成一个数字,表示该货币的编号.然后其实本题用到了类似Floyd的动态规划思想.

首先假设货币1对换货币2 比率为a,货币2对换货币3 比率为b.

那么货币1对换货币3比率为多少呢?为a*b.

现在我们希望货币能增值,所以如果货币1换货币3 有两种比率分别为0,5和0,6.那么我们明显放弃0.5那个,只需要用0.6的比率即可.所以这道题就成了求一个有向图的任意两点的最大兑换比例,不过这个比例不是相加运算了,而是相乘运算.且现在不是最小值最优了,而是最大值最优了。

找出最长路径的方法：

flody算法的变式

伪代码如下：

Floyd(A[1…n])

//生成有向图每个顶点之间的最长路径

//输入：一个有向图A

//输出：一个具有每个顶点之间最长距离的图A

for i ← 1 to n do

        for j ← 1 to n do

                for k ← to n do

                        if A[j][k] < A[j][i] * A[i][k])

                                        A[j][k] = A[j][i] * A[i][k]

首先通过map这种STL将每种货币代表的顶点号记录下来，生成货币与顶点之间的对应关系，根据题目给出的兑换率生成有向图。再通过Floyd算法生成有向图每个顶点之间的最长路径，判断对角线上的元素是否有大于1的，大于1说明有一条路径可以实现套汇。

三、结果及分析

样例1：

 

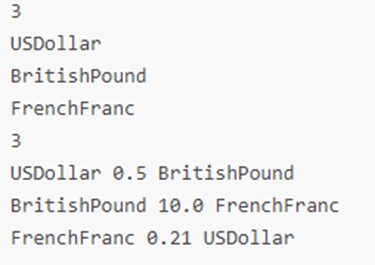
图 3 样例1

对应的二维数组为：

 

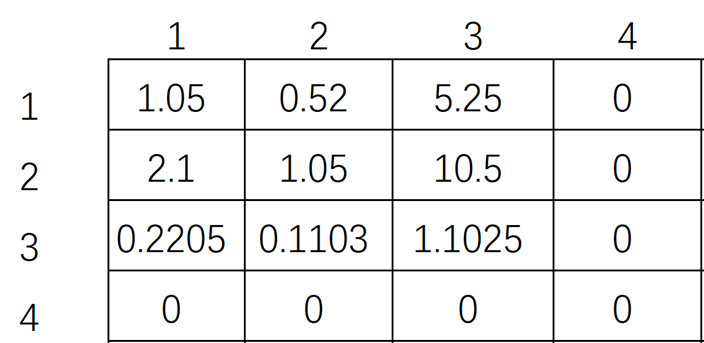
图 4 样例1对应的二维数组

通过样例1的二维数组我们可以看出对角线上的值存在大于1的，说明存在一种方式可以实现经过若干次兑换后，兑换成原来的货币可以使货币量增加。

样例2：

 

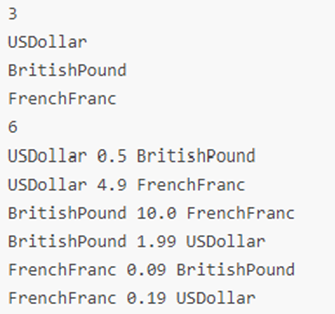
图 5 样例2

对应的二维数组为：

 

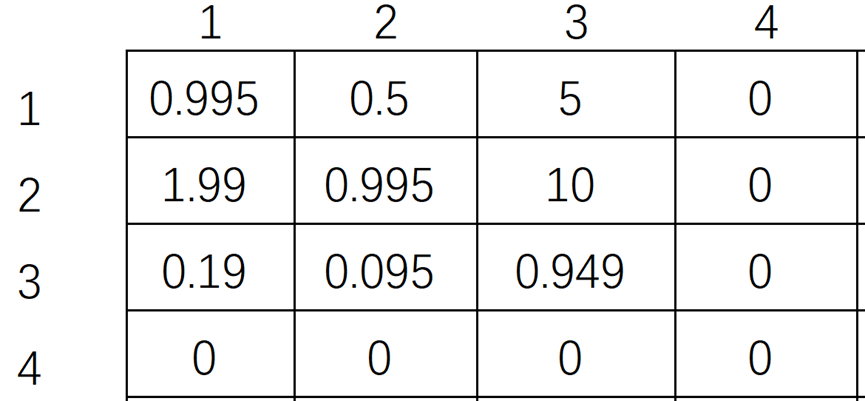
图 6 样例2对应的二维数组

通过样例2的二维数组我们可以看出对角线上的值不存在大于1的值，说明没有方法使得原来的货币量增加。

算法分析：

Floyd(A[1…n])

//生成有向图每个顶点之间的最长路径

//输入：一个有向图A

//输出：一个具有每个顶点之间最长距离的图A

for i ← 1 to n do   …………………………………………………………n

        for j ← 1 to n do ………………………………………………………n

                for k ← to n do ……………………………………………………n

                        if A[j][k] < A[j][i] * A[i][k])

                                        A[j][k] = A[j][i] * A[i][k]

Floyd算法复杂度为O(n^3)

所以改程序的时间复杂度为O(n^3)。

其他解法：

在网上看见有不同的解法，主要是使用了Bellman_Ford 来判断正环。

题意大致可以变成在一个n个顶点的图中能否找到一个正权环，这里的正权环指财富增加，很明显可用Bellman-ford 算法（专门解决存在环的最短路径问题）。

Bellman-ford 算法：一个具有n个顶点的图如果不存在环，则从顶点x,到顶点y，最多经过n-1条边（要考虑连通性，每个顶点最多经过 1 次），因此 x 到 y 的最短路 最多经过 n - 1 次松弛操作（就是更新长度）就应该出现，如果第 n 次松弛还可以得到最优，那么这个图就肯定是存在环了（直接用Dijkstra 就无法得到最优的，环的存在会影响最优解是否存在）。

 

图 7 Bellman-ford 算法 

四、总结

floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话，首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题，我们需要为这个目标重新做一个诠释。floyd算法加入了这个概念。

   (1) 用数组dis[i][j]来记录i,j之间的最短距离。初始化dis[i][j],若i=j则dis[i][j]=0,

若i,j之间有边连接则dis[i][j]的值为该边的权值，否则dis[i][j]的值为 。

   (2) 对所有的k值从1到n，修正任意两点之间的最短距离，计算dis[i][k]+dis[k][j]的值，若小于dis[i][j],则dis[i][j]= dis[i][k]+dis[k][j]，否则dis[i][j]的值不变。

 

 Bellman-Ford算法与Dijkstra算法思想一样，用于求解单源点最短路径问题。Bellman-ford算法除了可求解边权均非负的问题外，关键是还可以解决存在负权边的问题，而Dijkstra算法只能处理边权非负的问题，因此 Bellman-Ford算法的适用面要广泛一些。但是，原始的Bellman-Ford算法时间复杂度较高，应对于具体问题进行优化。

（1） 初始化：将除源点外的所有顶点的最短距离估计值 dist[v] ←+∞, dist[s] ←0;

（2）迭代求解：反复对边集E中的每条边进行松弛操作，使得顶点集V中的每个顶点v的最短距离估计值逐步逼近其最短距离；（运行|v|-1次）

（3）检验负权回路：判断边集E中的每一条边的两个端点是否收敛。如果存在未收敛的顶点，则算法返回false，表明问题无解；否则算法返回true，并且从源点可达的顶点v的最短距离保存在 dist[v]中。

 五、参考文献及附录

MojitoCoco 最短路径Floyd算法 [EB/OL] [2019-09-28].

https://www.bilibili.com/video/BV1LE411R7CS

 coderyzh 最短路径模板+解析——（FLoyd算法）[EB/OL] [2019-03-17].

https://blog.csdn.net/ytuyzh/article/details/88617987

 kewlgrl POJ 2240-Arbitrage [EB/OL] [ 2016-08-02 ]. https://blog.csdn.net/MIKASA3/article/details/52091567

 RioTian POJ：Arbitrage （搜索，汇率换算是否赚？） [EB/OL] [ 2020-05-19 ].

https://www.cnblogs.com/RioTian/p/12918264.html

 附录：

Floyd算法
#include<bits/stdc++.h>
#define INF 9999999
using namespace std;
double dp[33][33] = {0};
void f(int n) {
    for(int i = 0 ; i < n ; i++) {
        for(int j = 0 ; j  < n ; j++) {
            for(int k = 0 ; k < n ; k++) {
                if(dp[j][k] < dp[j][i] * dp[i][k]) {
                    dp[j][k] = dp[j][i] * dp[i][k];
                }
            }
        }
    }
}
int main() {
    int n,m,cnt = 1;
    double rate;
    map<string,int>g;
    while(cin >> n,n) {
        memset(dp,INF,sizeof(dp));
        for(int i =  0; i < n ; i++) {
            string s;
            cin >> s;
            g[s] = i;
        }
        cin >> m;
        for(int i = 0 ; i < m ; i ++) {
            string a,b;
            cin >> a >> rate >> b;
            dp[g[a]][g[b]] = rate;
        }
        f(n);
        int flag =0;
        for(int i = 0 ; i < n ; i++) {
            if(dp[i][i] > 1) {
                flag =1;
                break;
            }
        }
        if(flag) cout << "Case " << cnt++ << " Yes" << endl;
        else cout << "Case " << cnt++ << " No" << endl;
    }
}

Bellman_Ford算法
#include<bits/stdc++.h> 
using namespace std;
const int maxn = 40;
double d[maxn];
int n, m;

struct Edge {
    int u, v;
    double r;
} edge[maxn * maxn];
map<string, int>mp;

bool bellman_ford(int s) {
    memset(d, 0, sizeof(d));
    d[s] = 1;
    for(int i = 1; i <=n; ++i)
        for (int j = 0; j < m; ++j) {
            int u = edge[j].u;
            int v = edge[j].v;
            double r = edge[j].r;
            if (d[v] < d[u] * r)
                d[v] = d[u] * r;
        }
    if (d[s] > 1.0)return true;
    return false;
}

int main() {
    int cnt = 1;
    while (cin >> n && n) {
        mp.clear();

        string s;
        for (int i = 1; i <= n; ++i) {
            cin >> s;
            mp[s] = i;
        }

        cin >> m;
        string s1, s2;
        double rat;
        for (int i = 0; i < m; ++i) {
            cin >> s1 >> rat >> s2;
            edge[i].u = mp[s1];
            edge[i].v = mp[s2];
            edge[i].r = rat;
        }

        bool flag = false;
        for(int i = 1; i <=n; ++i)
            if (bellman_ford(i)) {
                flag = true;
                break;
            }

        if(flag) cout << "Case " << cnt++ << " Yes" << endl;
        else cout << "Case " << cnt++ << " No" << endl;
    }
}