【题解】#10249. 「一本通 1.3 例 5」weight

• #10249. 「一本通 1.3 例 5」weight题解

题意

【题目描述】
原题来自：USACO
已知原数列 \(a_1​,a_2​,\dots,a_n\)​ 中的前 1 项，前 2 项，前 3 项， 前 n 项的和，以及后 1 项，后 2 项，后 3 项，后 n 项的和，但是所有的数都被打乱了顺序。此外，我们还知道数列中的数存在于集合 S 中。试求原数列。当存在多组可能的数列时，求字典序最小的数列。

【输入格式】
第 1 行，一个整数 n 。
第 2 行，2×n 个整数，注意：数据已被打乱。
第 3 行，一个整数 m ，表示 S 集合的大小。
第 4 行， m 个整数，表示 S 集合中的元素。

【输出格式】
输出满足条件的最小数列。

【数据范围】
对于 100% 的数据， 1≤n≤1000,1≤m≤500 ，且 S∈{1,2,⋯,500} 。

思路

要成为一名合格的OIer,您首先要学会倒着思考。（所谓倒着并不是指倒立）：
很明显，给定了和的集合后，加以排序，每个位置上的数都确定了。故用深搜找出符合条件的数列即可。
对于每一个被拎出来的数，它只有可能被放在数列的前半段（顺着搜）或后半段（倒着搜）。于是我们在dfs函数中用两个参数x、y记录分别顺着/倒着搜到哪，当x==y且剩下待填入的数在数集S里时，说明找到了目标数列，输出即可。
字典序？暂时不会证[笑哭]，持续更新……

顺便说一句，笔者在理解题解的时候有如下抽风行为：

1. \(S_n\)=\(T_n\)， 即前缀和与后缀和中，各自的最大值相等
   很明显，数列\(a_1, a_2 , \dots ,a_n\)一共有\(n\)项。

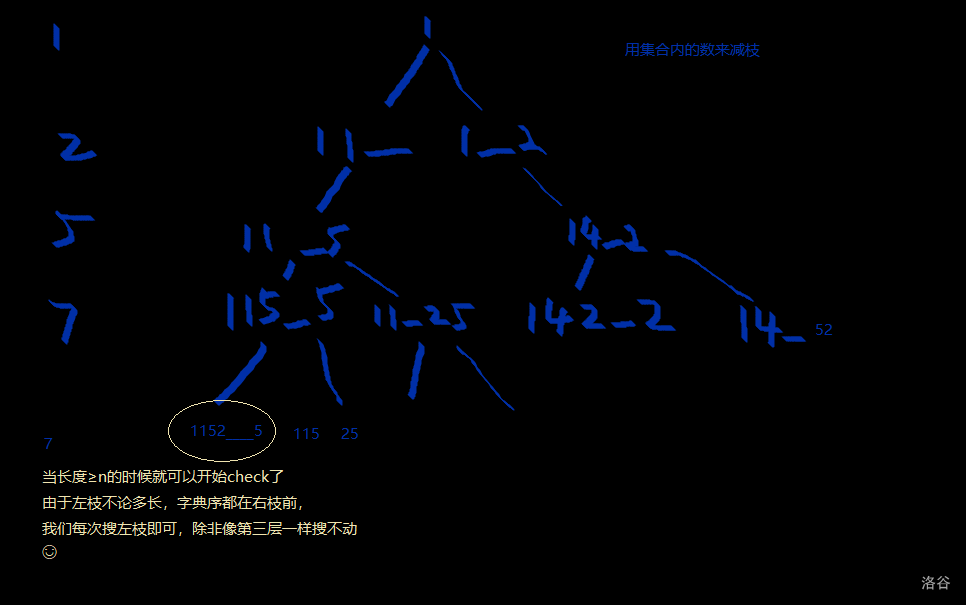
看起来很棒，但是不能满足字典序最小。
为什么？其实笔者还不知道。

代码实现

x. seq1[p1]=0
最后一道关卡：下载大样例后发现总是有一处输出0，逐段排查后发现是回溯时加上seq[p]=0这一句导致的。但是按理说，已经回溯了，不影响呀？
究其原因，是不太聪明的笔者把seq[p]=0放在了p--后面……直接导致了RE和WA……这个故事告诉我们，做题的时候要集中精力！不要边听信(y)息(z)老(j)师催眠边写，除非您有足够的时间、精力和耐心找这个低级错误。

♪(＾∀＾●)ﾉ撒花~

AC Code

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=2005;
int n,m;
ll s[N];
ll p,seq1[N],p1,seq2[N],p2;
bool a[N],flag;

void dfs(int k,int x,int y,ll pre,ll suf) {
	if(flag) return;
	if(x==y) {
		if((!a[s[k]-pre]) && (!a[s[k]-suf])) return;
		if(s[2*n]<=suf+pre || s[2*n]-pre-suf>500) return;
		if(!a[s[2*n]-suf-pre]) return;
		for(int i=1; i<=p1; i++) printf("%lld ",seq1[i]);
		printf("%lld ",s[2*n]-suf-pre);
		for(int i=p2; i>=1; i--) printf("%lld ",seq2[i]);
		flag=true;
		return;
	}
	if(s[k]>pre && s[k]-pre<=500) {
		if(a[s[k]-pre]) {
			p1++;
			seq1[p1]=s[k]-pre;
			dfs(k+1,x+1,y,s[k],suf);
			if(flag) return;
			p1--;
		}
	}
	if(s[k]>suf && s[k]-suf<=500) {
		if(a[s[k]-suf]) {
			p2++;
			seq2[p2]=s[k]-suf;
			dfs(k+1,x,y-1,pre,s[k]);
			if(flag) return;
			p2--;
		}
	}
}

int main() {
	scanf("%d",&n);
	for(int i=1; i<=2*n; i++) scanf("%lld",&s[i]);
	scanf("%d",&m);
	for(int i=1,j; i<=m; i++) {
		scanf("%d",&j);
		a[j]=true;
	}
	sort(s+1,s+2*n+1);
	dfs(1,1,n,0,0);//the first element of set a,now filling the yth space,current sum
	return 0;
}
/*
5
1 2 5 7 7 9 12 13 14 14
4
1 2 4 5
*/
//2022.03.03,finally!!!!!!!