最小生成树

最小生成树

 一、什么是图的最小生成树（MST）？

   　　不知道大家还记不记得树的一个定理：N个点用N-1条边连接成一个连通块，形成的图形只可能是树，没有别的可能。

 

一个有N个点的图，边一定是大于等于N-1条的。图的最小生成树，就是在这些边中选择N-1条出来，连接所有的N个点。这N-1条边的边权之和是所有方案中最小的。

 

 

二、最小生成树用来解决什么问题？

就是用来解决如何用最小的“代价”用N-1条边连接N个点的问题。例如：

【例4-9】、城市公交网建设问题

【问题描述】

　　有一张城市地图，图中的顶点为城市，无向边代表两个城市间的连通关系，边上的权为在这两个城市之间修建高速公路的造价，研究后发现，这个地图有一个特点，即任一对城市都是连通的。现在的问题是，要修建若干高速公路把所有城市联系起来，问如何设计可使得工程的总造价最少？

【输入格式】

    n（城市数，1<=n<=100）

　　e（边数）

　　以下e行，每行3个数i,j,wij，表示在城市i,j之间修建高速公路的造价。

【输出格式】

　　n-1行，每行为两个城市的序号，表明这两个城市间建一条高速公路。

【输入样例】

　　5 8

　　1 2 2

　　2 5 9

　　5 4 7

　　4 1 10

　　1 3 12

　　4 3 6

　　5 3 3

　　2 3 8

【输出样例】

　　　1  2

　　　2  3

　　　3  4

　　　3  5

 

【分析】：

对于最小生成树问题，有两种解决方法，*Prim*与*Kruskacl*，复杂度分别为O(m*logn) O(m*logm)，一下是对其两种算法的简单介绍

 

Kruskal算法

Kruskal（克鲁斯卡尔）算法是一种巧妙利用并查集来求最小生成树的算法。

　　首先我们把无向图中相互连通的一些点称为处于同一个连通块中。例如下图

图中有3个连通块。1、2处于一个连通块中，4、5、6也处于一个连通块中，孤立点3也称为一个连通块。

Kruskal算法将一个连通块当做一个集合。Kruskal首先将所有的边按从小到大顺序排序（一般使用快排），并认为每一个点都是孤立的，分属于n个独立的集合。然后按顺序枚举每一条边。如果这条边连接着两个不同的集合，那么就把这条边加入最小生成树，这两个不同的集合就合并成了一个集合；如果这条边连接的两个点属于同一集合，就跳过。直到选取了n-1条边为止。

 

算法描述:

 

1. 初始化并查集。father[x]=x，
2. tot=0
3. 将所有边用快排从小到大排序。
4. 计数器 k=0;
5. for (i=1; i<=M; i++)      //循环所有已从小到大排序的边

 

if 这是一条u,v不属于同一集合的边(u,v)(因为已经排序，所以必为最小)，

 

    　①合并u,v所在的集合，相当于把边(u,v)加入最小生成树。

 

　    ②tot=tot+W(u,v)

 

      ③k++

 

      ④如果k=n-1,说明最小生成树已经生成，则break;

 

1. 结束，tot即为最小生成树的总权值之和。

 

 

 

【思想讲解】

 

Kruskal（克鲁斯卡尔）算法开始时，认为每一个点都是孤立的，分属于n个独立的集合。

 

 

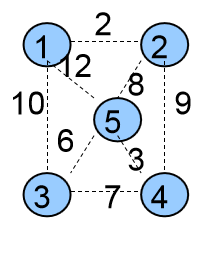
5个集合{ {1}，{2}，{3}，{4}，{5} }

 

生成树中没有边

 

 

 

Kruskal每次都选择一条最小的边，而且这条边的两个顶点分属于两个不同的集合。将选取的这条边加入最小生成树，并且合并集合。

 

第一次选择的是<1,2>这条边，将这条边加入到生成树中，并且将它的两个顶点1、2合并成一个集合。

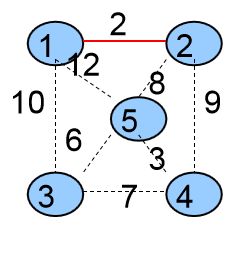
4个集合{ {1，2}，{3}，{4}，{5} }

生成树中有一条边{ <1,2> }

第二次选择的是<4,5>这条边，将这条边加入到生成树中，并且将它的两个顶点4、5合并成一个集合。

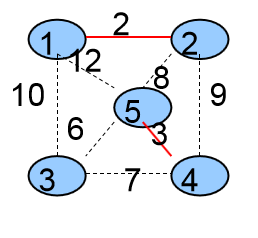
3个集合{ {1，2}，{3}，{4，5} }

生成树中有2条边{ <1,2> ，<4,5>}

第三次选择的是<3,5>这条边，将这条边加入到生成树中，并且将它的两个顶点3、5所在的两个集合合并成一个集合　　

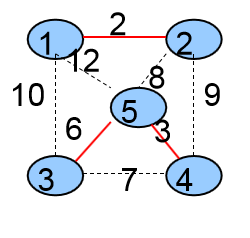
2个集合{ {1，2}，{3，4，5} }

生成树中有3条边{ <1,2> ，<4,5>，<3，5>}

第四次选择的是<2,5>这条边，将这条边加入到生成树中，并且将它的两个顶点2、5所在的两个集合合并成一个集合。　　

 

 

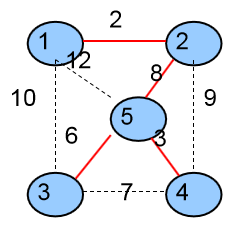
1个集合{ {1，2，3，4，5} }

生成树中有4条边{ <1,2> ，<4,5>，<3，5>，<2,5>}

  算法结束，最小生成树权值为19。

　　通过上面的模拟能够看到，Kruskal算法每次都选择一条最小的，且能合并两个不同集合的边，一张n个点的图总共选取n-1次边。因为每次我们选的都是最小的边，所以最后的生成树一定是最小生成树。每次我们选的边都能够合并两个集合，最后n个点一定会合并成一个集合。通过这样的贪心策略，Kruskal算法就能得到一棵有n-1条边，连接着n个点的最小生成树。

　　Kruskal算法的时间复杂度为O(E*logE)，E为边数。

程序如下：

#include<cstdio>
#include<iostream>
#include<algorithm>
#define N 5005
#define M 200010
#define FORa(i,s,e)    for(i=s;i<=e;i++)
#define FORs(i,s,e)    for(i=s;i>=e;i--)
#define File(name) freopen(name".in","r",stdin); freopen(name".out","w",stdout);
using namespace std;
static char buf[100000],*pa=buf,*pb=buf;
#define gc pa==pb&&(pb=(pa=buf)+fread(buf,1,100000,stdin),pa==pb)?EOF:*pa++
inline int read();
struct Edge{
    int next,from,to,dis;
}edge[N];
int head[10000],n,m,num_edge,fa[N];
bool bz[N];
int find(int x)
{
    if(fa[x]==x)
        return fa[x];
    fa[x]=find(fa[x]);
}
void Add_edge(int from,int to,int dis)
{
    edge[++num_edge]=(Edge){head[from],from,to,dis};
    head[from]=num_edge;
}
bool cmp(Edge p1,Edge p2)
{
    p1.dis<p2.dis;
}
int main()
{
    File("Kruskal");
    int from,to,fdis,i,tot=0,sum=0,t1,t2;
    n=read(),m=read();
    FORa(i,1,n) fa[i]=i;
    FORa(i,1,m)
    {
        from=read(),to=read(),fdis=read();
        Add_edge(from,to,fdis);
        Add_edge(to,from,fdis);
    }
    sort(edge+1,edge+1+n,cmp);
    bz[1]=1;
    FORa(i,1,m)
    {
        t1=find(edge[i].from),t2=find(edge[i].to);
        if(t1!=t2)
        {
            fa[t1]=fa[t2];
            tot++;
            sum+=edge[i].dis;
        }    
        if(tot==n-1) break;
    }
    if(tot==n-1)
    cout<<sum;
    else
        cout<<"orz";
    return 0;
}
inline int read()
{
    register int x(0);register int f(1);register char c(gc);
    while(c<'0'||c>'9')f=c=='-'?-1:1,c=gc;
    while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=gc;
    return f*x;
}

int Find(int x) 并差集 压缩路径

{if(fa[x]==x) return x;fa[x]=Find(fa[x]);}

 

FORa(i,1,n) fa[i]=i; 初始化，将父亲指向自己

sort(edge+1,edge+1+n,cmp);排序

FORa(i,1,m)

{

t1=Find(edge[i].from);t2=Find(edge[i].to);

if(t1!=t2) 并差集合并

cnt++,fa[t1]=t2,ans+=edge[i].dis;

if(cnt==n-1)

cout<<ans;return;

 

Prim算法

Prim算法采用与Dijkstra、Bellman-Ford算法一样的“蓝白点”思想：白点代表已经进入最小生成树的点，蓝点代表未进入最小生成树的点。

算法描述：

以1为起点生成最小生成树，min[v]表示蓝点v与白点相连的最小边权。MST表示最小生成树的权值之和。

一：初始化：min[v]= ∞(v≠1); min[1]=0;MST=0;

二：for (i = 1; i<= n; i++)

1.寻找min[u]最小的蓝点u。

2.将u标记为白点

3.MST+=min[u]

4.for 与白点u相连的所有蓝点v  

  if (w[u][v]<min[v])

 min[v]=w[u][v];

三：算法结束： MST即为最小生成树的权值之和

 

算法分析&思想讲解：

   Prim算法每次循环都将一个蓝点u变为白点，并且此蓝点u与白点相连的最小边权min[u]还是当前所有蓝点中最小的。这样相当于向生成树中添加了n-1次最小的边，最后得到的一定是最小生成树。

　我们通过对下图最小生成树的求解模拟来理解上面的思想。蓝点和虚线代表未进入最小生成树的点、边；白点和实线代表已进入最小生成树的点、边。

初始时所有点都是蓝点，min[1]=0,min[2、3、4、5]=∞。权值之和MST=0。

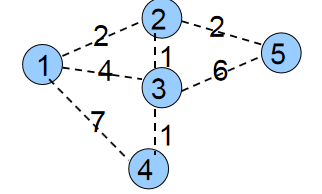
第一次循环自然是找到min[1]=0最小的蓝点1。将1变为白点，接着枚举与1相连的所有蓝点2、3、4，修改它们与白点相连的最小边权。

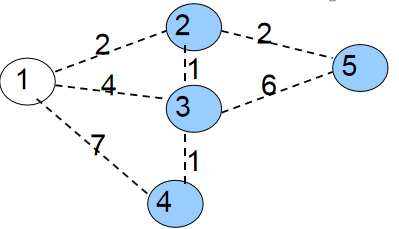
min[2]=w[1][2]=2;

min[3]=w[1][3]=4;

min[4]=w[1][4]=7；

第二次循环是找到min[2]最小的蓝点2。将2变为白点，接着枚举与2相连的所有蓝点3、5，修改它们与白点相连的最小边权。

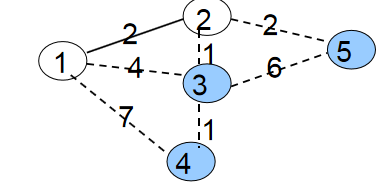
min[3]=w[2][3]=1;

min[5]=w[2][5]=2;

　　

第三次循环是找到min[3]最小的蓝点3。将3变为白点，接着枚举与3相连的所有蓝点4、5，修改它们与白点相连的最小边权。

 

min[4]=w[3][4]=1;

由于min[5]=2 < w[3][5]=6;所以不修改min[5]的值。

最后两轮循环将点4、5以及边w[2][5],w[3][4]添加进最小生成树。

 

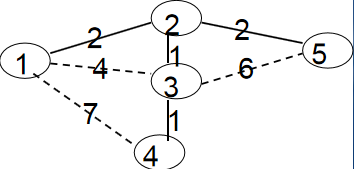
最后权值之和MST=6。这n次循环，每次循环我们都能让一个新的点加入生成树，n次循环就能把所有点囊括到其中；每次循环我们都能让一条新的边加入生成树，n-1次循环就能生成一棵含有n个点的树；每次循环我们都取一条最小的边加入生成树，n-1次循环结束后，我们得到的就是一棵最小的生成树。这就是Prim采取贪心法生成一棵最小生成树的原理。算法时间复杂度：O (N2)。

 

#include<cstdio>
#include<queue>
#include<cstring>
#include<utility>
#include<algorithm>
#define FORa(i,s,e) for(i=s;i<=e;i++)
#define R register int
using namespace std;

int n,m,cnt,ans,head[5005],dis[5005],bz[5005]; 
struct Edge
{
    int next,to,dis;
}edge[400005];
int num_edge;
void Add_edge(int from,int to,int dis)
{
    edge[++num_edge]=(Edge){head[from],to,dis};
    head[from]=num_edge;
}
typedef pair <int,int> pp;
priority_queue <pp,vector<pp>,greater<pp>> q;//first dis     second u
void Prim()
{
    pp ft;
    dis[1]=0;
    q.push(make_pair(0,1));
    while(!q.empty()&&cnt<n)
    {
    ft=q.top(),q.pop();
        if(bz[ft.second]) continue;
        cnt++,ans+=ft.first,bz[ft.second]=1;
        for(R i=head[ft.second];i;i=edge[i].next)
            if(dis[edge[i].to]>edge[i].dis)
                dis[edge[i].to]=edge[i].dis,q.push(make_pair(dis[edge[i].to],edge[i].to));
    }
}
int main()
{
    memset(dis,127,sizeof(dis));
    R from,to,fdis;
    scanf("%d%d",&n,&m);
    for(R i=1;i<=m;i++)
    {
        scanf("%d%d%d",&from,&to,&fdis);
        Add_edge(to,from,fdis),Add_edge(from,to,fdis);
    }
    Prim();
    if (cnt==n)printf("%d",ans);
    else printf("orz");
}

 

#define PP pair<int,int>二元组存储最小生成树的信息

priority_queue<PP,vector<PP>,greater<PP>> q; 放入优先队列中，链式前向星储存，降低时空复杂度

memset(dis,63,sizeof(dis)); dis[1]=0; 赋初值

q.push(make_pair(0,1)); 随便将一个点插入队列

while(!q.empty()&&cnt<n)

{

p=q.top(),q.pop();  取出蓝点中离最小生成树最小的点

if(bz[p.second]) continue;判重

cnt++,ans+=p.first,bz[p.second]=1;

for(i=head[p.second];i;i=edge[i].next)

if(edge[i].dis<dis[edge[i].to])  类似dijkstra的松弛操作，更新蓝点离最小生成树的距离

dis[edge[i].to]=edge[i].dis,q.push(make_pair(edge[i].dis,edge[i].to));

}

if(cnt==n) cout<<ans; 是否生成一颗最小生成树

 

【总结】

克鲁斯卡尔

1. 并查集加排序
2. 预处理，现将所有的节点的父亲指向自己
3. 输入m条边，切记，只需要m条边
4. 按每一条边的权值排序
5. 最后并查集来查询，看是否加入到生成树中，注意并查集模板是这样写的

int Find(int x){if(fa[x]==x) return fa[x];  return fa[x]=Find(fa[x]);

1. 最后查看是否是构造了一颗n个点，n-1条边的最小生成树

普里姆

1. 对于构造边，就使用链式前向星，但是对于边的话就需要开两倍
2. 初始化，将dis[]（这个点到最小生成树的最近的距离）赋值为一个极大的值，但是不能超过INF的二分之一，即为memset(dis,63,sizeof (dis))为一个较大的值，memset赋值的时候需要赋值为2的x次方-1
3. 再用一个pair来储存队列节点的信息，宏定义 #define pair<int,int> pp
4. 放入优先队列priority_queue<pp,vector<pp>,greater<pp> >  q; 小根堆，默认为大根堆
5. 两个连着的尖括号之间需要打空格
6. Pair的比较，先比较first，在比较second，所以将dis存入first，u存入second
7. 最外层循环为队列不为空且最小生成树还没有构建好while(!q.empty()&&cnt<n)
8. 接着，退出队列中的对头，查看是否出现过，没有出现过就将此点打标记，cnt++，答案加上这条边的权值，扩散连接它的边，放入队列

 感谢各位与信奥一本通的鼎力相助！