NNDL 神经网络与深度学习 第3章 线性模型（上）——学习笔记

现在我们才算正式开始学习 神经网络与深度学习 的内容

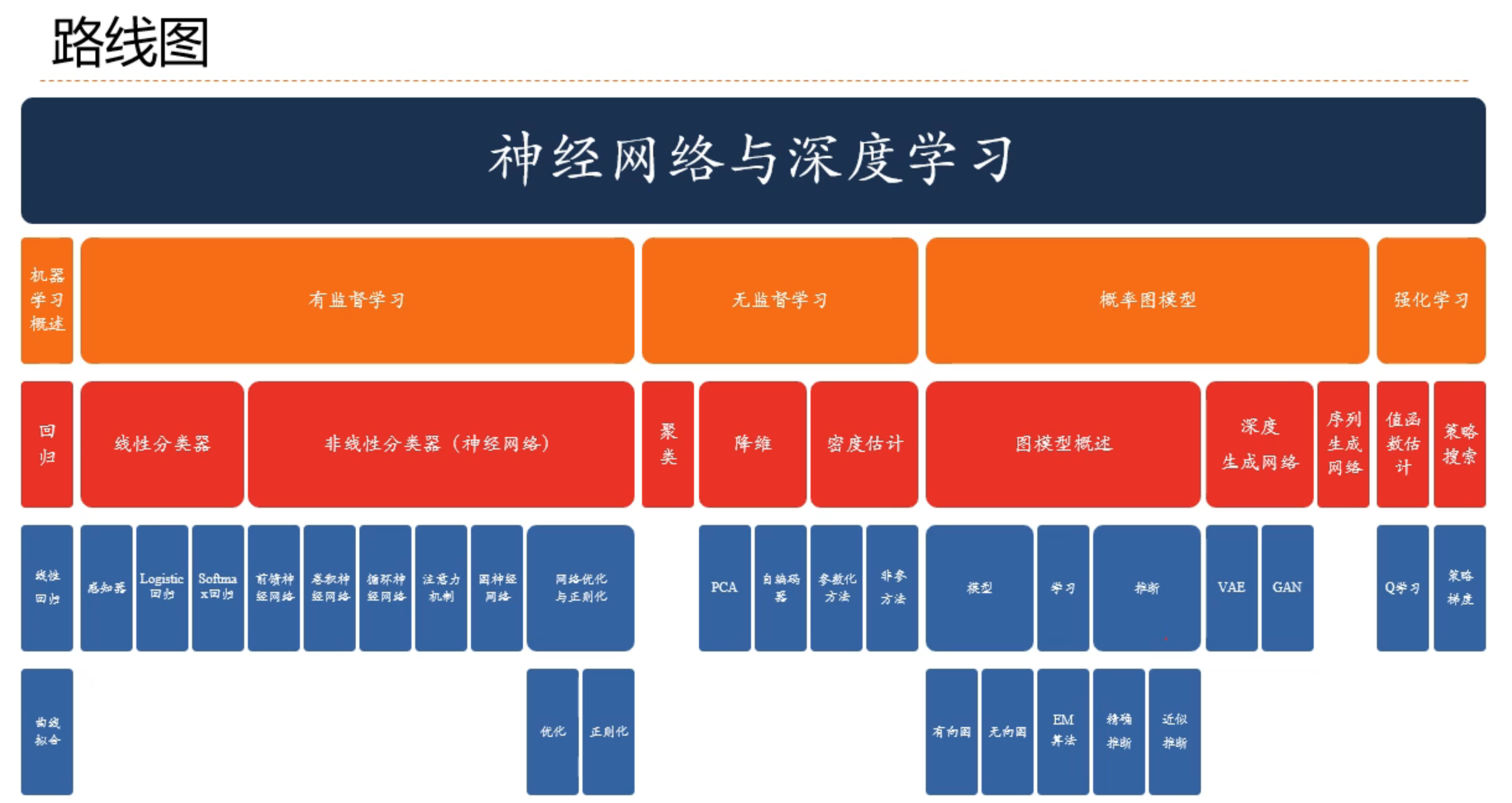
线性模型

线性模型（Linear Model）是机器学习中应用最广泛的模型，指通过样本特征的线性组合来进行预测的模型．给定一个 𝐷 维样本 𝒙 = [𝑥1, ⋯ , 𝑥𝐷]T，其线性组合函数为:

其中 𝒘 = [𝑤1, ⋯ , 𝑤𝐷]T 为 𝐷 维的权重向量，𝑏 为偏置。

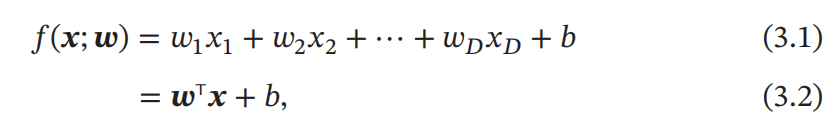
我们先以典型的线性模型——线性回归来讲解

线性回归（Linear Regression）

回归 （Regression）

回归问题的输入 x 为 𝐷 维向量，输出 y 为 一个连续变量。主要表示的是求解 x，y之间的映射关系。

模型

线性回归的模型为：

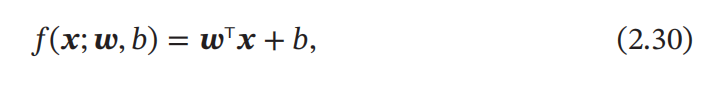
b 为什么叫偏置，因为如果没有 b 整个模型其实是过原点的。而我们可以通过方法将偏置消除掉，那么我们就要介绍 增广权重向量 和 增广特征向量（如下图）：

他们其实都是对 x 和 w 的变换。 我们直接将 **增广权重向量 和 增广特征向量 与 x、w 替代**，那么我们可以将整个线性回归模型 简化为： 𝑓(𝒙 ; 𝒘) = 𝒘T𝒙．

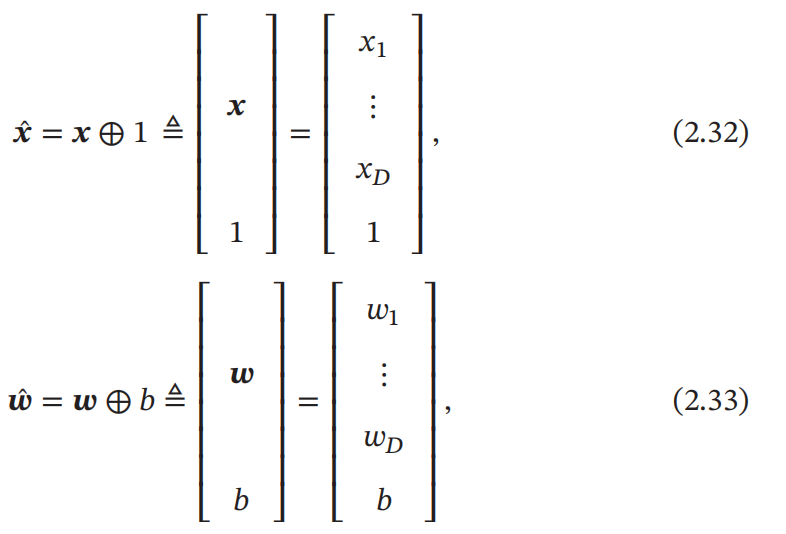
通过增广向量可以将线性回归的偏置消除

经验风险最小化（ERM）

经验风险

上一章我们介绍到，平方损失函数适合于预测标签 y 为实数值的任务中，而线性回归预测标签 y 为连续实数值，因此平方损失函数非常合适衡量真实标签和预测标签之间的差异。所以我们可以定义训练集 D 上的经验风险为：

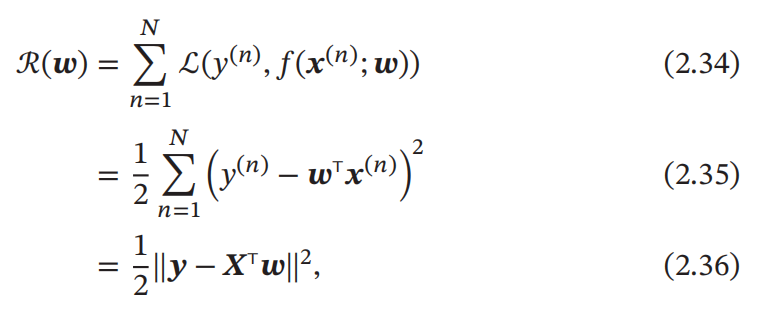
其中最后一个式子，是我们对其进行的简化:

其中 𝒚 = [𝑦⁽¹⁾, ⋯ , 𝑦^(𝑁)]^T ∈ ℝ^𝑁 是由所有样本的真实标签组成的列向量。

而 𝑿 ∈ ℝ^{(𝐷+1)×𝑁} 是由所有样本的输入特征 𝒙⁽¹⁾, ⋯ , 𝒙^(𝑁) 组成的矩阵：

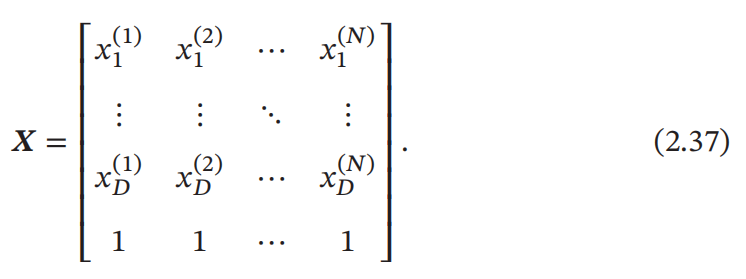
风险最小化

我们得到了经验风险的式子，那么我们需要对其进行最小化，这里就需要涉及求矩阵偏导的基础知识。

矩阵微积分

标量关于向量的偏导数：

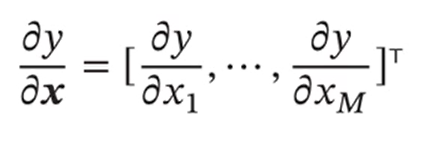
向量关于向量的偏导数：

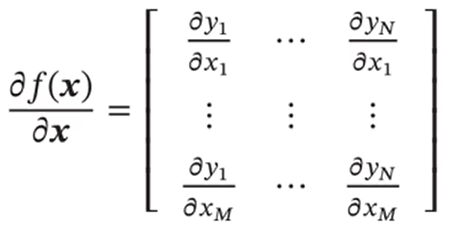
向量函数及其导数：

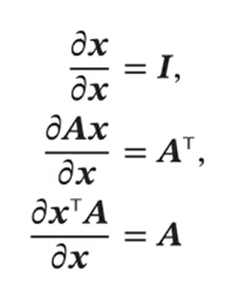
求解

风险函数 ℛ(𝒘) 是关于 𝒘 的凸函数，其对 𝒘 的偏导数为：

令 $$\frac{𝜕}{𝜕𝒘}R(𝒘)= 0$$ 得到最优的参数𝒘∗ 为

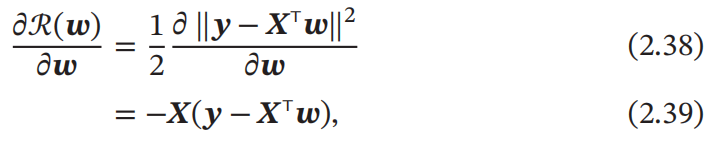
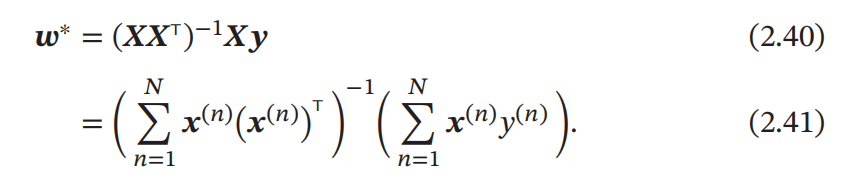
这种求解线性回归参数的方法也叫最小二乘法（Least Square Method，LSM）

结构风险最小化

结构风险

最小二乘法的基本要求是各个特征之间要互相独立，保证 $𝑿𝑿^T$ 可逆。但即使 $𝑿𝑿^T$ 可逆，如果特征之间有较大的多重共线性（Multicollinearity），也会使得 $𝑿𝑿^T$ 的逆在数值上无法准确计算。数据集 $𝑿$ 上一些小的扰动就会导致 ${{(𝑿𝑿^T)}^{−1}}$ 发生大的改变，进而使得最小二乘法的计算变得很不稳定。于是提出了岭回归（Ridge Regression）,加上一个常数 $𝜆$ 使得 $(𝑿𝑿^T + 𝜆𝐼)$ 满秩，即其行列式不为 $0$ 得到：

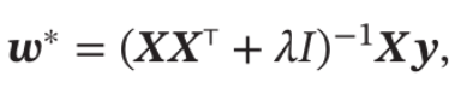
岭回归的解 $𝒘^∗$ 可以看作结构风险最小化准则下的最小二乘法估计，其目标函数可以写为

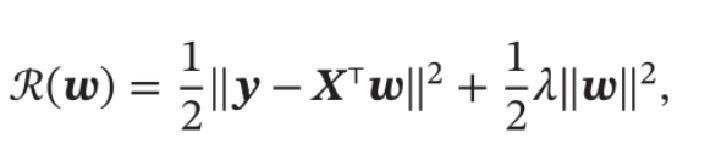
线性回归的概率视角

基本概念

• 概率（Probability）：一个随机事件发生的可能性大小，为0到1之间的实数。

• 随机变量（Random Variable）：比如随机掷一个骰子，得到的点数就可以看成一个随机变量X，其取值为{1,2,3,4,5,6}。

• 概率分布（Probability Distribution）：一个随机变量 $X$ 取每种可能值的概率。

  • ${P(X = x_i) = p(x_i)}$   ${\forall{i}\in{\{1,...,n\}}}$
  • 满足 $\sum\limits_{i=1}^{n}p(x_i) = 1$, ${p(x_i)\geqslant0}$，${\forall{i}\in{\{1,...,n\}}}$

• 伯努利分布（Bernoulli Distribution）：在一次试验中，事件A出现的概率为µ，不出现的概率为1 − µ。若用变量X 表示事件A出现的次数，则X 的取值为0和1，其相应的分布为：

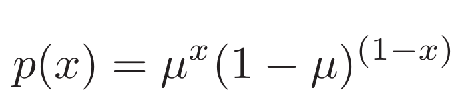
• 二项分布（Binomial Distribution）：在n次伯努利分布中，若以变量X 表示事件A出现的次数，则X 的取值为 $\{0,… ,n\}$，分布为：

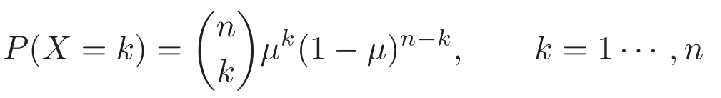
二项式系数，表示从n个元素中取出k个元素而不考虑其顺序的组合的总数。

• 连续随机变量 𝑌 的概率分布一般用概率密度函数（ Probability Density Function ， PDF ）p(x) 来描述。

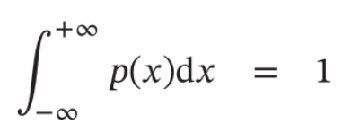
• 高斯分布（Gaussian Distribution）：统计学上又叫正态分布，高斯函数是正态分布的密度函数，分布为：

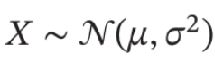
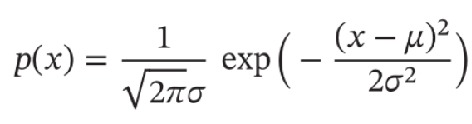
• 贝叶斯公式：两个条件概率p(y|x)和p(x|y)之间的关系：

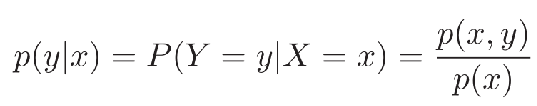
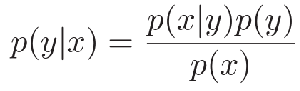
最大似然估计

从概率的角度来看线性回归，本来标签 ${y = f(x;w)}$，但是我们加入一个噪声${\varepsilon\sim{N(0,\sigma^2)}}$，那么${y = f(x;w)+\varepsilon}$，我们就可以将 $y$ 看作一个随机变量，其服从以均值为$f(x;w) = w^Tx$，方差为 $σ^2$ 的高斯分布。

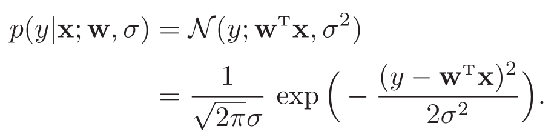
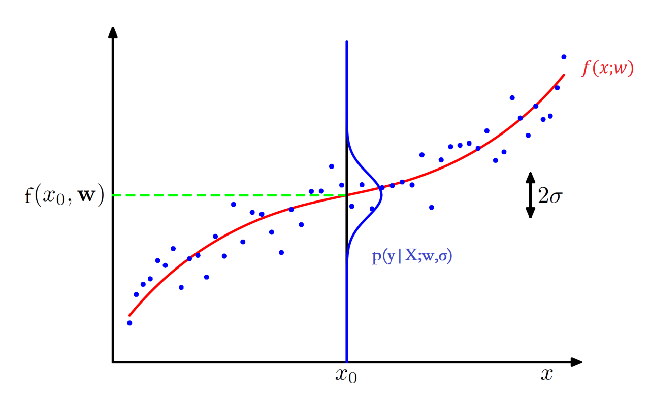
有了概率模型之后，我们就需要求解模型参数，我们引入了似然这个概念。

似然

似然函数是关于统计模型 ${p(x;w)}$ 的参数 $w$ 的函数。

• $w$ 固定时，我们称 ${p(x;w)}$ 为概率，它描述固定参数 $w$ 时，随机变量 $x$ 的分布情况。
• $w$ 变动时，我们称 ${p(x;w)}$ 为似然，它描述已知随机变量 $x$ 时，不同参数 $w$ 对其分布的影响。

机器学习一般是求解 $w$ ，所以提出了似然，它其实和概率只是变量不同，研究对象不同。

线性回归中的似然

参数w在训练集D上的似然函数（Likelihood）为：

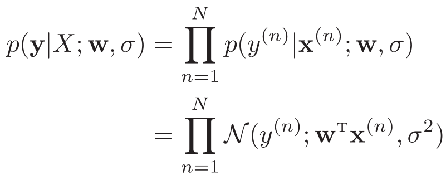
机器学习都假设数据独立同分布的。

最大似然估计（Maximum Likelihood Estimate，MLE）

定义了似然函数，我们还需要一个方法来优化参数 $w$。即是指找到一组参数 $w$ 使得似然函数 $p(y|X;w,σ)$ 最大。也就是给定 $x$ 找到一个 $w$ ，让 $y$ 的正确概率最大。

由于概率一般都比较小，所以进行了一定的对数处理。然后得到解，神奇的发现其实就是最小二乘法的解。

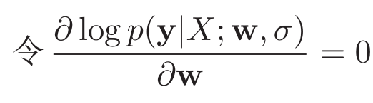
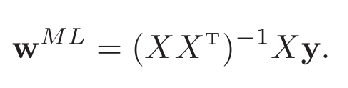
贝叶斯学习

我们用似然函数，将 $w$ 作为研究对象，来求解它。但实际上 $w$ 和 $x$ 都是随机变量，于是我们使用贝叶斯学习，将两个都看成随机变量来研究。它的目标是，给定一组观测数据 $X$ 求参数 $w$ 的分布 $p(w|X)$，$p(w|X)$ 也称为后验分布（posterior）
于是我们得到了，他们之间的关系。

最大后验估计（Maximum A Posterior Estimate，MAP）

找到一个 $w$ 使得 后验最大。

总结

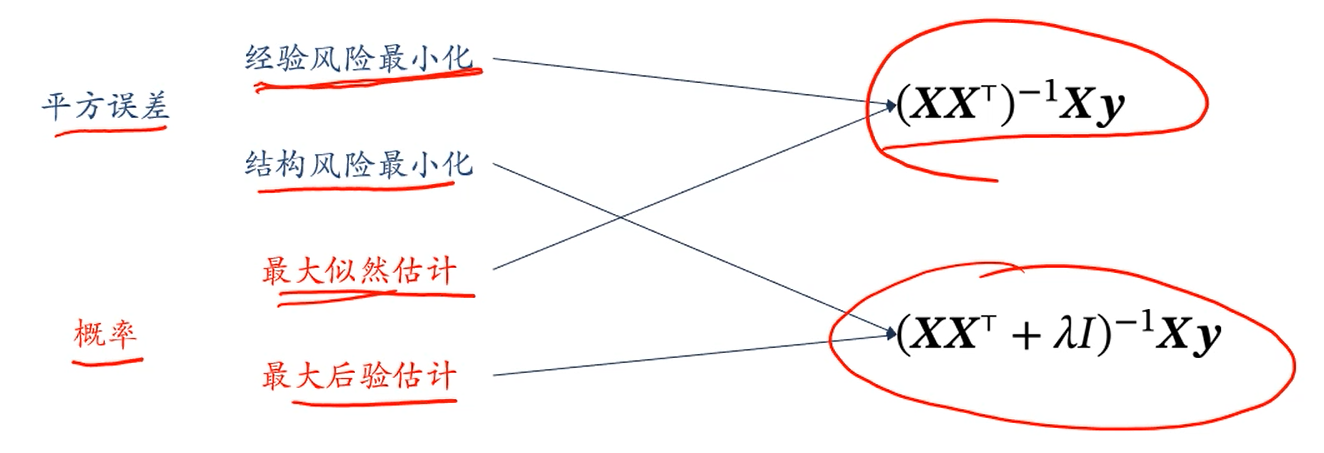
我们可以发现，平方误差角度和概率角度，它们其实都是等价的。