基础概念
数据集划分
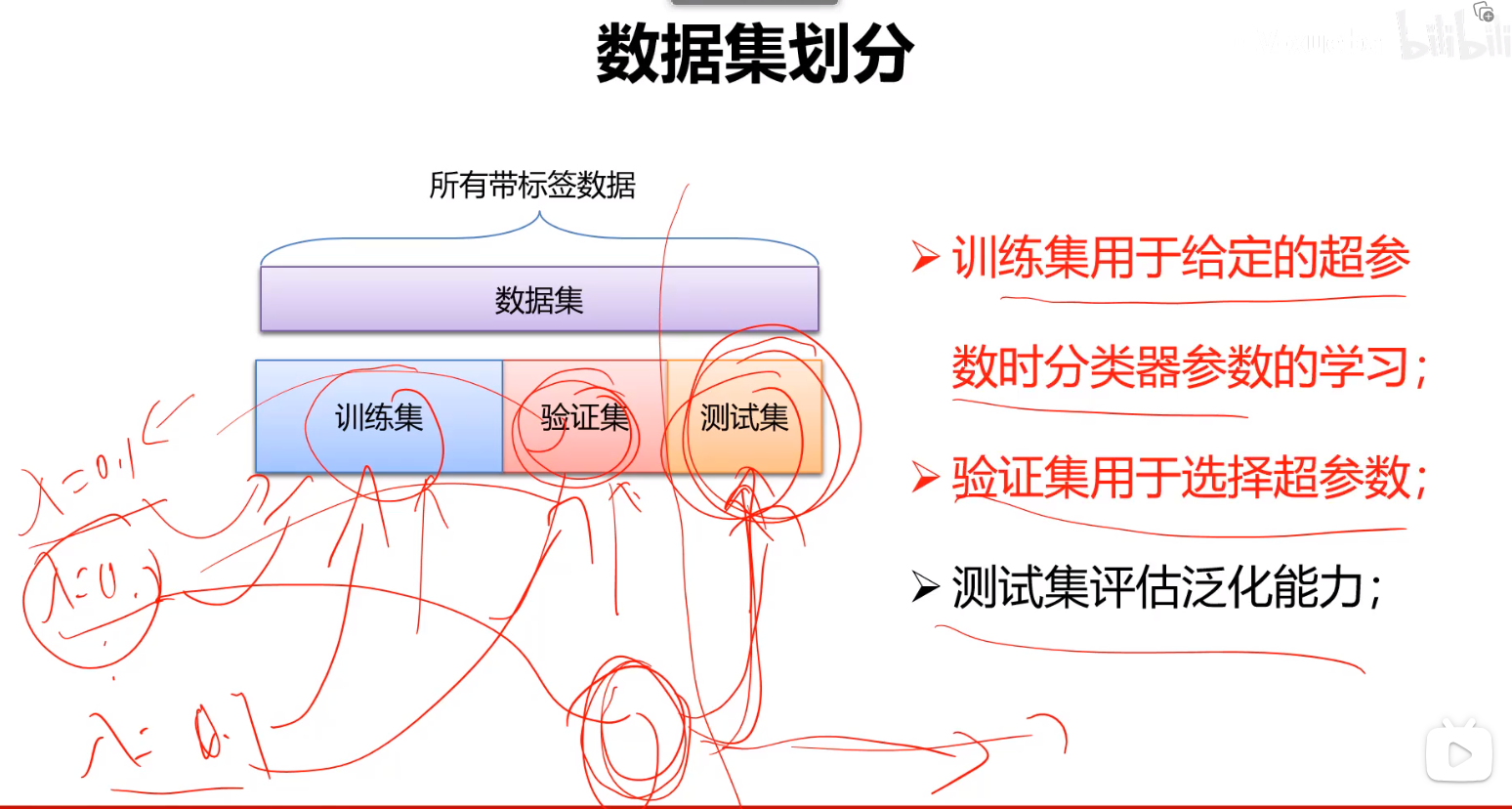
首先人为给定一组包括λ在内的,也就给定了一组模型,然后我们再确定参数的初值并带入训练集去优化每个模型的参数,然后将这些模型分别用验证集验证,看看哪个超参数对应的模型最好就将其带入测试集评价我现在能拿到最好模型的性能。
交叉验证

- 比如说做一个男女分类问题,一个模型对于男生的分类正确率为90%,对女生的分类正确率为90%;另外一个模型对于男生的分类错误率为100%,对于对女生的分类正确率为100%;如果选择的验证集全都是女生,我们肯定会得出第二个模型较好。
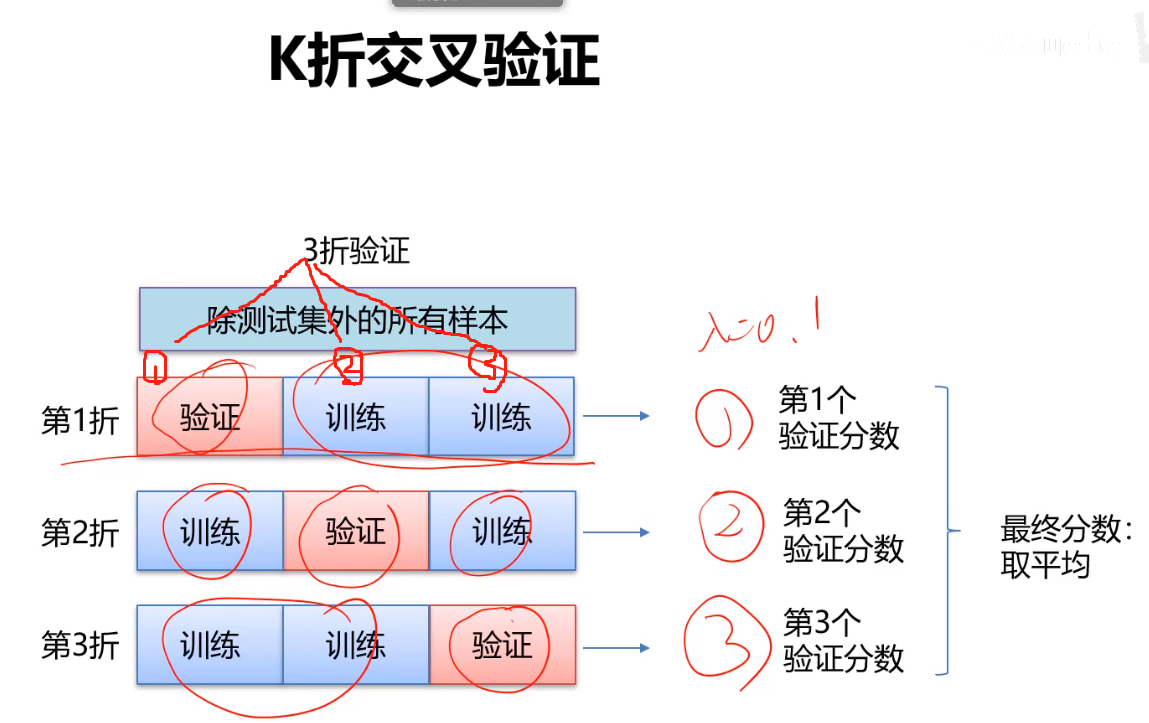
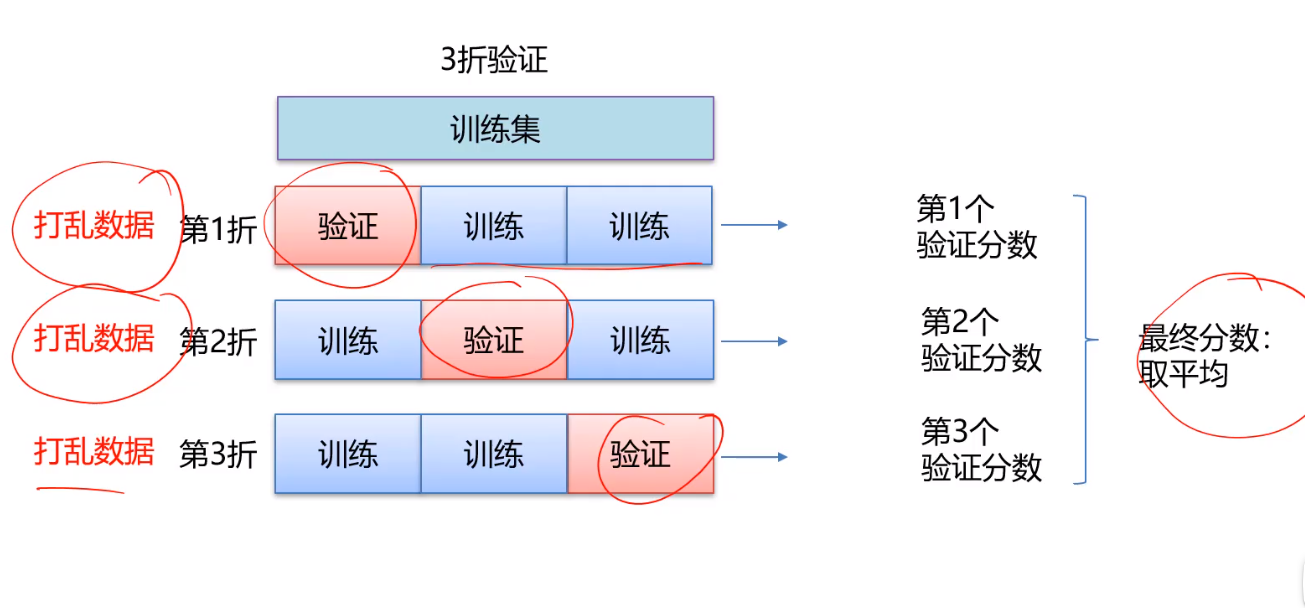
- 怎么发现问题,就是将训练集以不同方式划分,这次选择训练集中的一组数据为验证集,下次选择另外一组,如果对于同一个超参数的模型,发现这个模型在两组验证集的差别特别大,这个时候表明选择的验证集可能有问题
解决上述问题我们采用交叉验证的方法
数据预处理
归一化
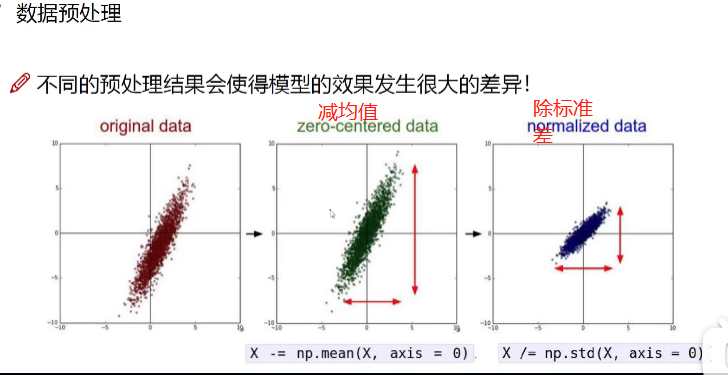
我们一般会将输入样本特征进行归一化处理,使数据变为均值为0,标准差为1的分布或者范围在0~1的分布。
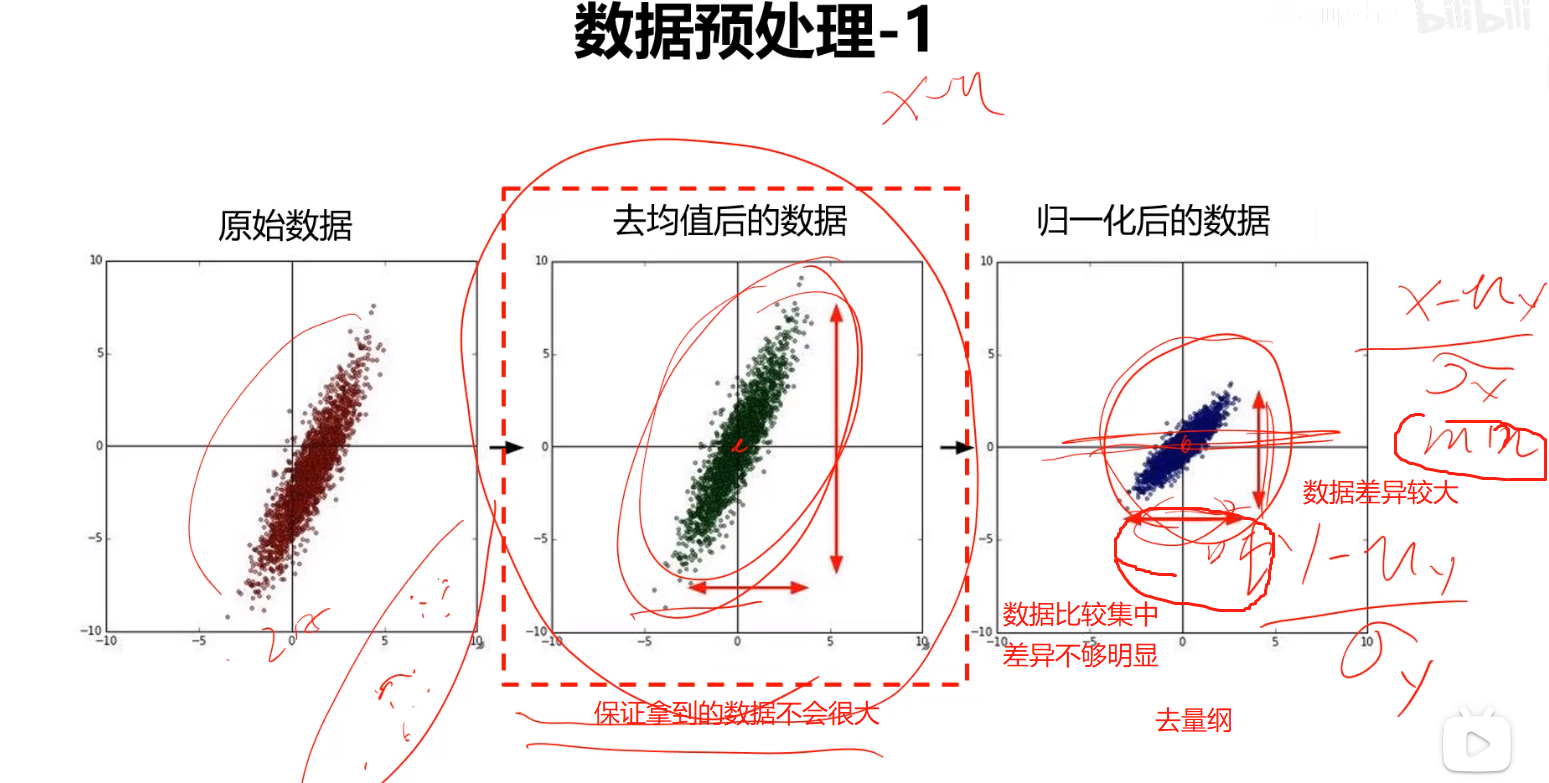
作用是:
- 保证输入的样本数据不会很大
- 去除量纲
- 防止网络因样本特征分布较散,使得神经网络学习速度缓慢甚至难以学习。
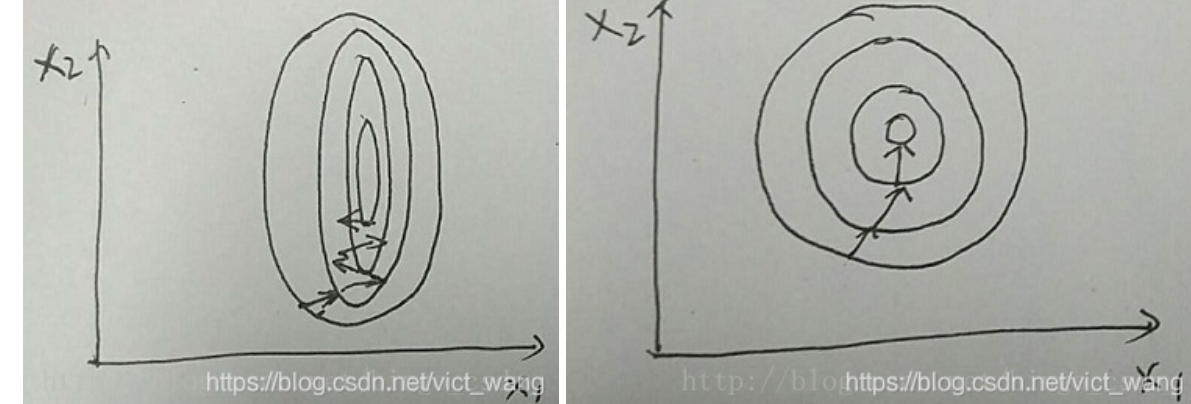
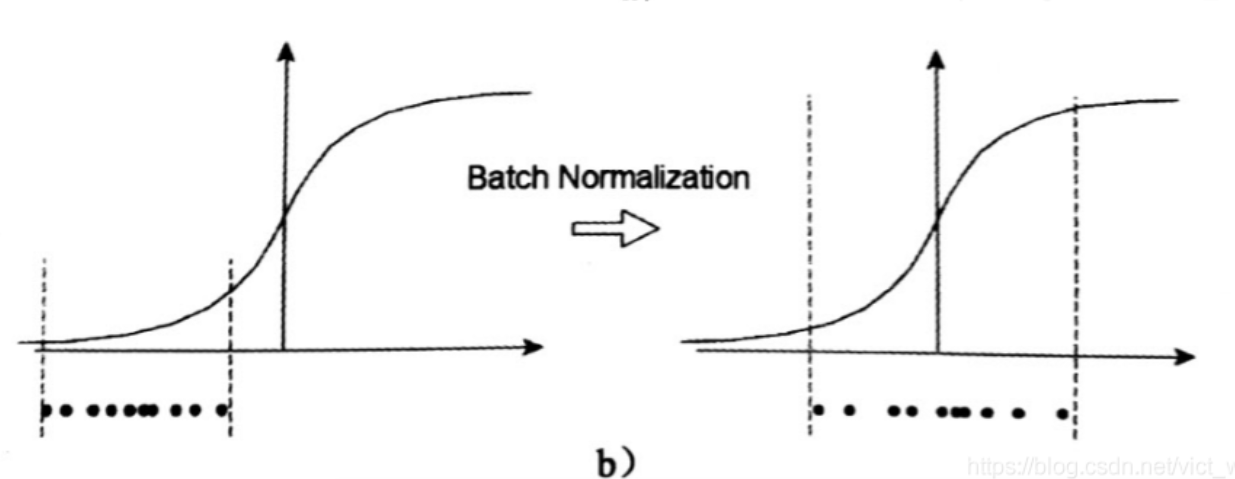
左图中样本特征的分布为椭圆,当用梯度下降法进行优化学习时,其优化过程将会比较曲折,需要经过好久才能到达最优点;右图中样本特征的分布为比较正的圆,当用梯度下降法进行优化学习时,其有过的梯度方向将往比较正确的方向走,训练比较快就到达最优点。因此一个比较好的特征分布将会使神经网络训练速度加快,甚至训练效果更好。
- 防止梯度消失
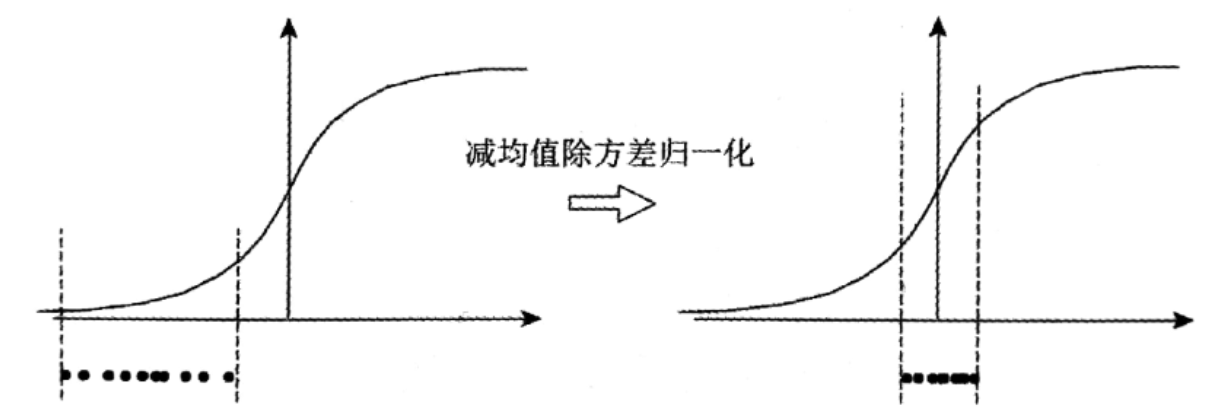
左图是没有经过任何处理的输入数据,曲线是sigmoid函数,如果数据在梯度很小的区域,那么学习率就会很慢甚至陷入长时间的停滞。减均值除方差后,数据就被移到中心区域如右图所示,对于大多数激活函数而言,这个区域的梯度都是最大的或者是有梯度的(比如ReLU),这可以看做是一种对抗梯度消失的有效手段。对于一层如此,如果对于每一层数据都那么做的话,数据的分布总是在随着变化敏感的区域,相当于不用考虑数据分布变化了,这样训练起来更有效率。
上述方法的缺点:
批归一化

注意批归一化的输入是指Wx,也就是将权值和输入数据相乘然后相加之后的值作为批归一化的输入
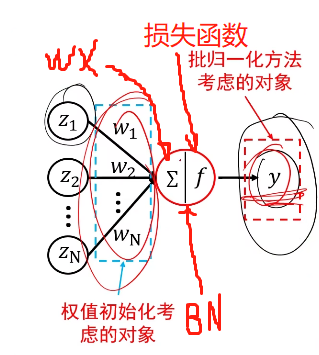
- 求每一个小批量训练数据的均值
- 求每一个小批量训练数据的方差
- 使用求得的均值和方差对该批次的训练数据做归一化,获得0-1分布。其中ε是为了避免除数为0时所使用的微小正数。
- 尺度变换和偏移:将xi乘以γ调整数值大小,再加上β增加偏移后得到yi,这里的γ是尺度因子,β是平移因子。这一步是BN的精髓,由于归一化后的xi基本会被限制在正态分布下,使得网络的表达能力下降。为解决该问题,我们引入两个新的参数:γ,βγ和β是在训练时网络自己学习得到的。
BN的本质就是利用优化变一下方差大小和均值位置,使得新的分布更切合数据的真实分布,保证模型的非线性表达能力。BN的极端的情况就是这两个参数等于mini-batch的均值和方差(μB,σ2B)那么经过batch normalization之后的数据和输入完全一样,当然一般的情况是不同的。
预测时均值和方差怎么求?
在训练时,我们会对同一批的数据的均值和方差进行求解,进而进行归一化操作。
但是对于测试时我们的均值和方差怎么求呢?由于测试的时候是用一张图像一张图像的去测试的,而批归一化的均值和方差是一批图像中求得的。
对于预测阶段时所使用的均值和方差,其实也是来源于训练集。比如我们在模型训练时我们就记录下每一批下的均值和方差,待训练完毕后,我们求整个训练样本的均值和方差期望值,作为我们进行预测时进行BN的的均值和方差,然后γ和β是我们训练的时候学习好的:
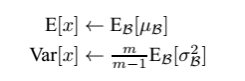
最后测试阶段,BN的使用公式就是:
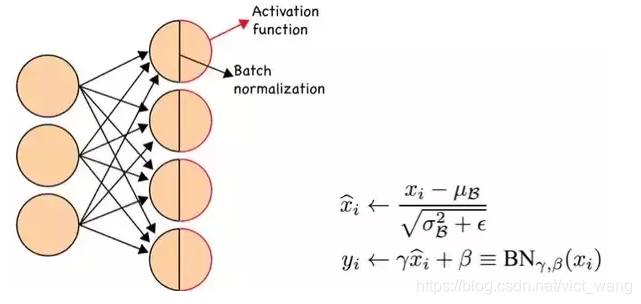
关于BN的使用位置,在CNN中一般应作用与非线性激活函数之前,s型函数s(x)的自变量x是经过BN处理后的结果。因此前向传导的计算公式就应该是:
![]()
其实因为偏置参数b经过BN层后其实是没有用的,最后也会被均值归一化,当然BN层后面还有个β参数作为偏置项,所以b这个参数就可以不用了。因此最后把BN层+激活函数层就变成了:

参考文章:
【深度学习】批归一化(Batch Normalization)_数据增强方法 批归一化_wuxiaoxiao2021的博客-CSDN博客
批归一化中的γ和β可用链式法则求得:
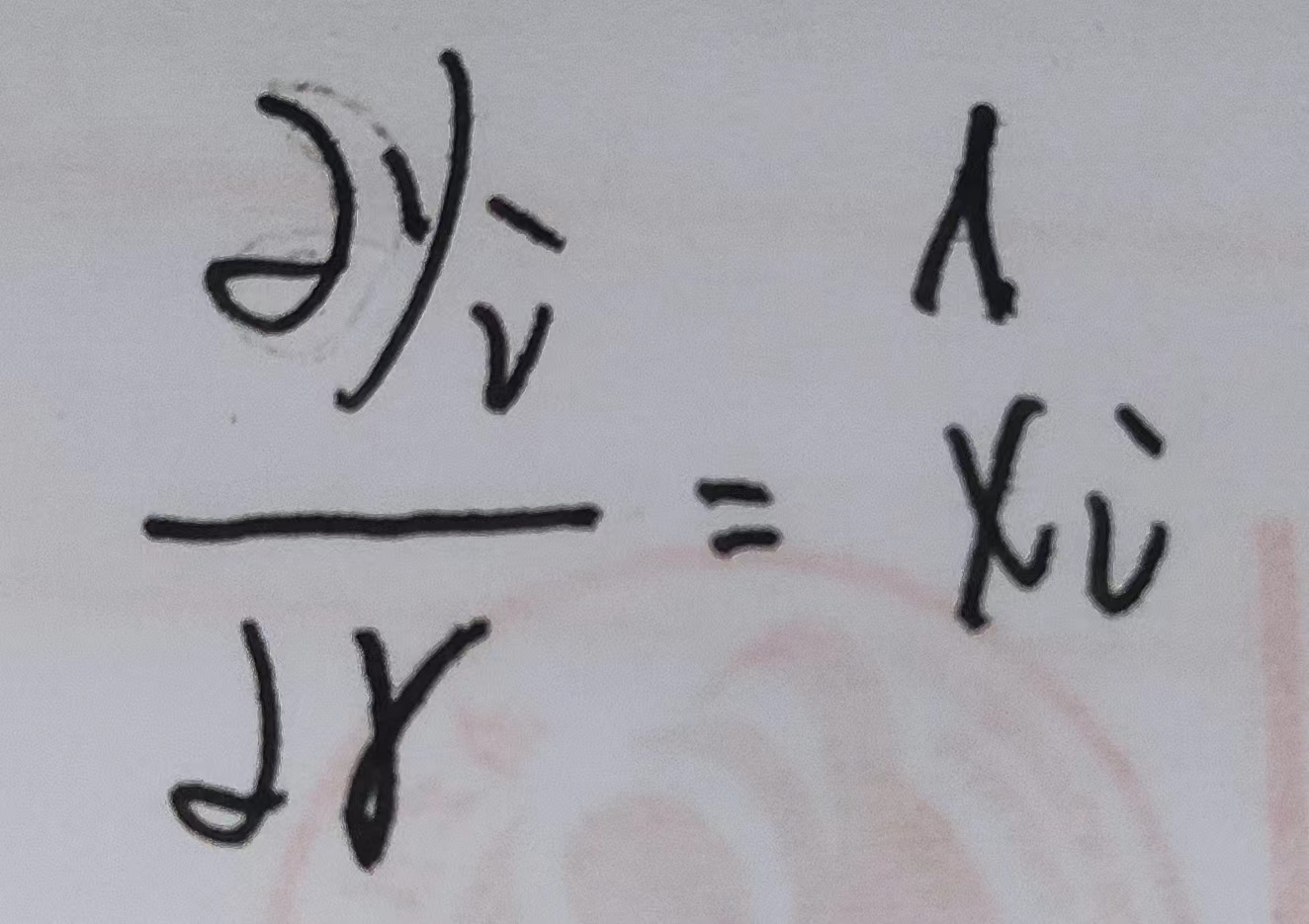
参数的初始化

权值初始化
全零初始化
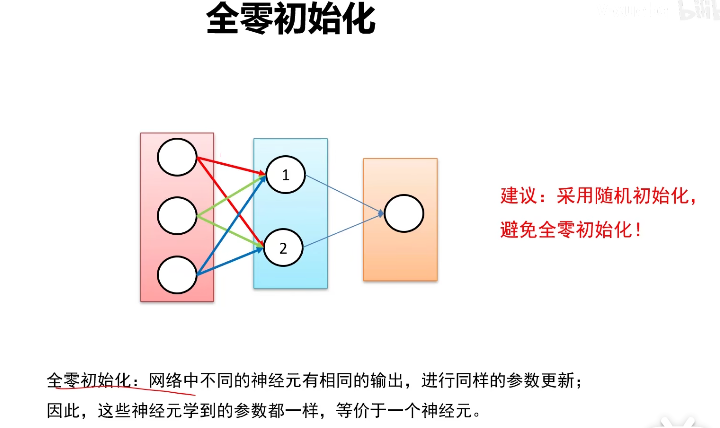
这样会导致每层的各个神经元的输出都一样,返回来的梯度都一样,更新过后的权值也都一样,这不是我们希望的结果。
上述权值不一定全都为0,全都为相同的值也会导致每次更新后的权值都一样

随机权值初始化

小方差的情况(会造成前向堵塞)
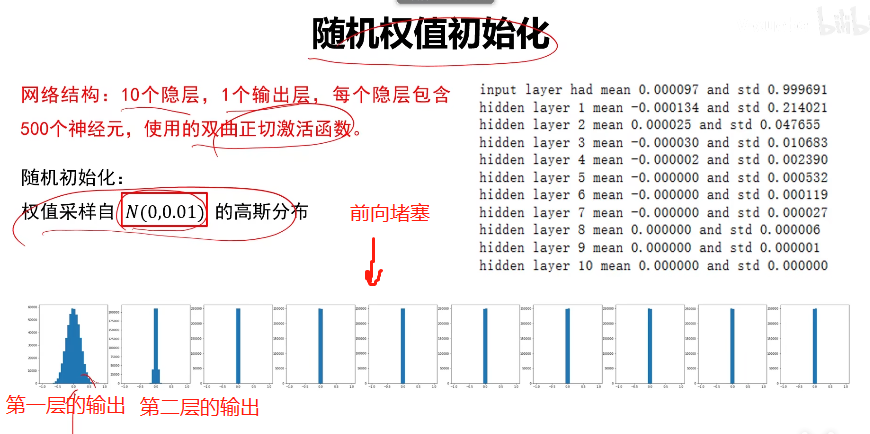
后面的输出基本都是0
大方差(方向堵塞,反向传递的时候梯度为0)
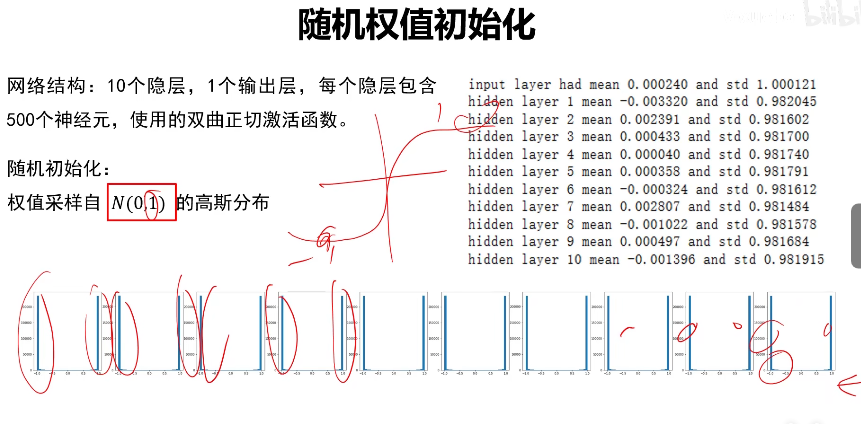
输出值都为±1,输出值如果在±1的话那么梯度就会为0,这会导致梯度消失。
Xavier初始化

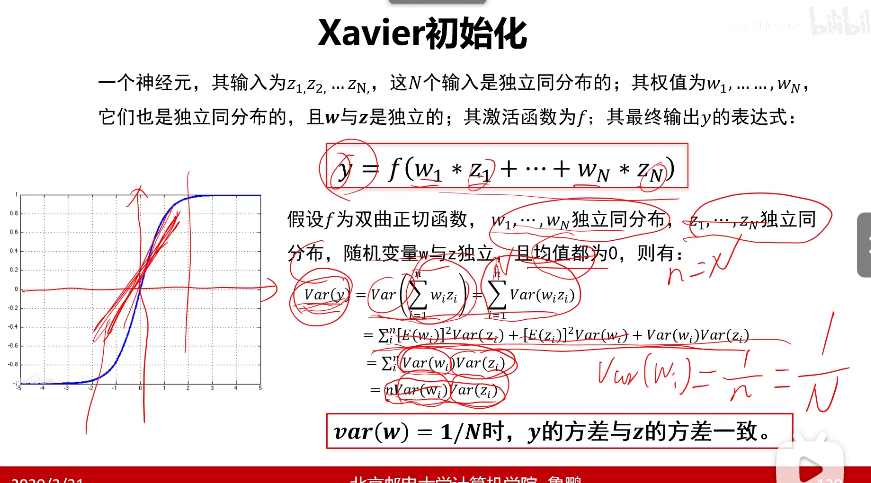

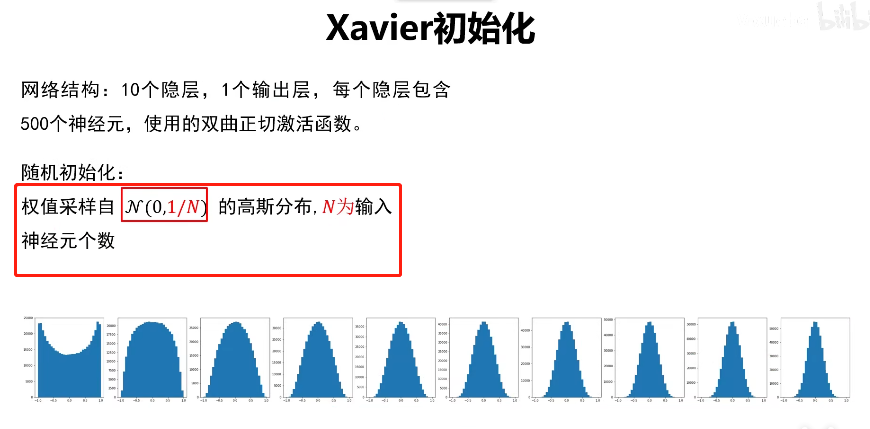
但是Xavier对Relu激活函数效果不大好
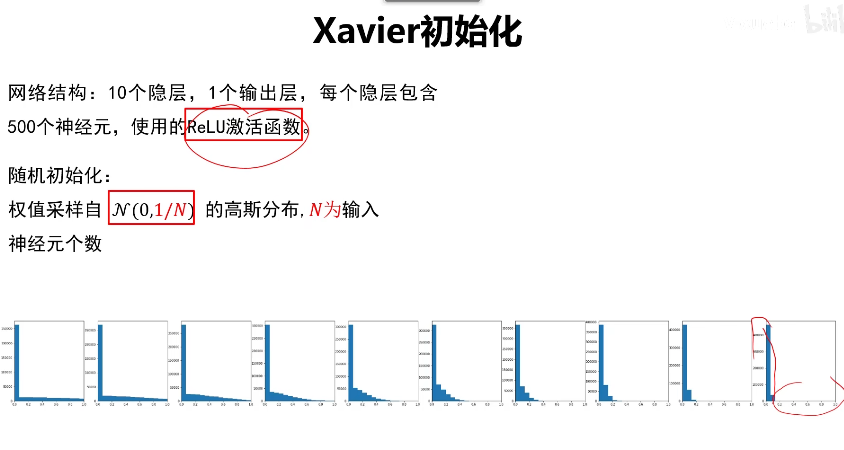
HE初始化
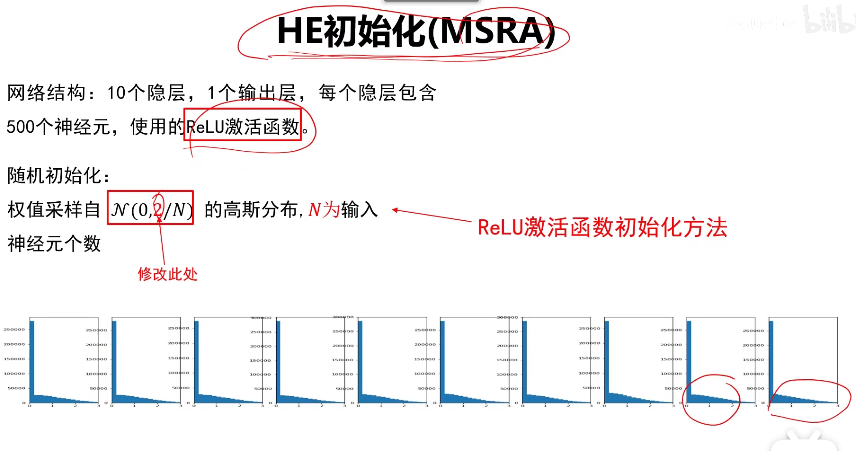

线性分类器(Wx+b的形式)
得分函数

W:权重参数,对结果起着决定性的影响因素,决定了模型的样子。权重的大小指的是这个像素的影响程度的大小,权重的正负表示对结果起着促进作用还是抑制作用,W的维度是类别数*特征维度
b:偏置参数,对结果进行微调操作,只是改变了模型的平移情况


权值可以看成模板,模板参与线性分类器运算时要变成向量,假如x和W2这个模板相乘后的值比较大,那么汽车这个类的模板最终得分肯定高,代表x越有可能时汽车类,也就是说如果x和模板相匹配的话,两者乘出来的结果肯定大
W矩阵是优化得来的
损失函数
用来衡量当前模型的好坏程度

策略就是用不同的数据集也就是用多张图片去验证这个分类器,每张图片的验证都会得到一个损失,然后将所有图片得到的损失累加然后取平均。
下面是一张图片的例子:



- 这个损失函数是大于0的,数值越大表明我们求得的权重矩阵越不好,在计算损失函数之前我们知道我们的输入是什么(有标签),比如我们输入的是猫,那么猫的那一维就是正确的得分,我们希望它比其它的维度的值要大
- 1表示容忍值,比如猫和车的得分过于接近这种情况下我们得到的损失是0,没有损失,这显然是我们不能容忍的,因为这样会导致我们将猫和汽车归为一类,因此我们得有一个容忍值,这样保证了当正确的数值要比错误的数值大多少我们才能认为是没有损失的。比如是这里是1,表明了正确的得分要比错误的得分大1,我们才能得到一个比1大的负数,导致结果是0,从而没有损失
正则化
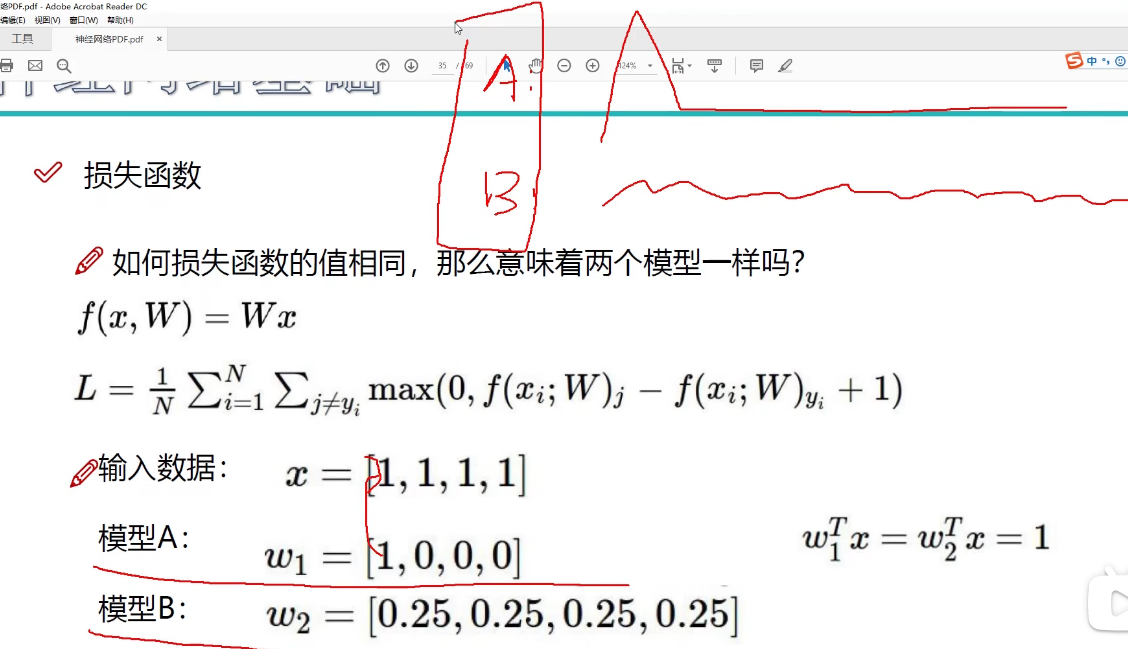
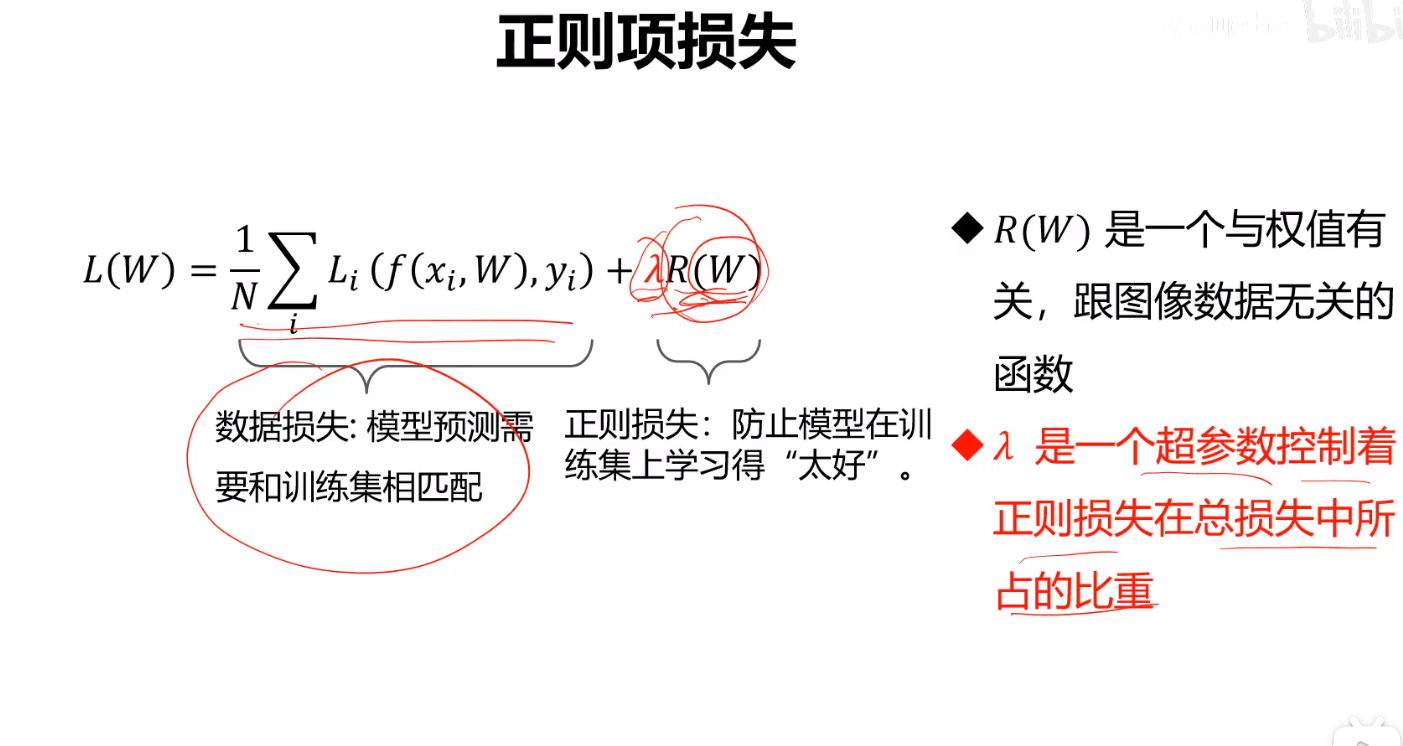
模型A只考虑x中第一个像素值因此容易发生过拟合,因此我们要加入正则化项,它代表了由于权重参数所带来的损失
超参数


超参数是学习之前就设置好的,它不需要通过学习而改变,而参数是学习之前给一个初始值,然后通过学习来改变这个参数以达到最优,神经元的个数以及神经元的层数(我们训练之前就设置好的)为超参数,神经元的权值(w)为参数
超参数的设置

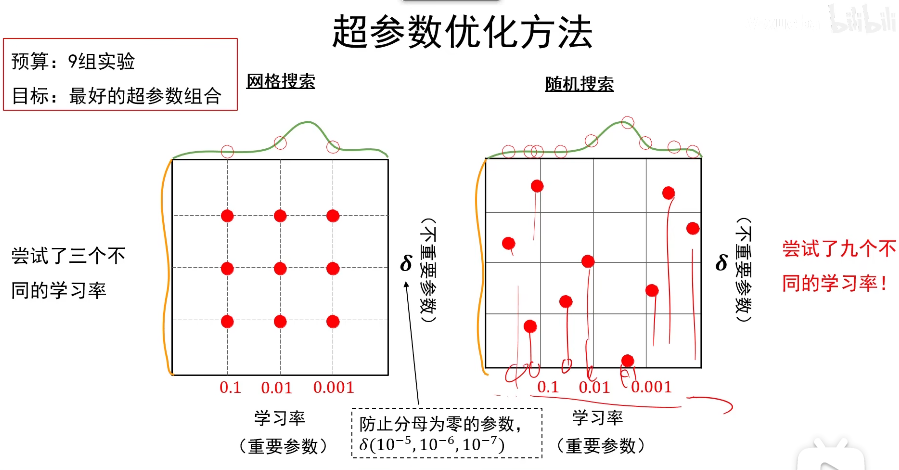
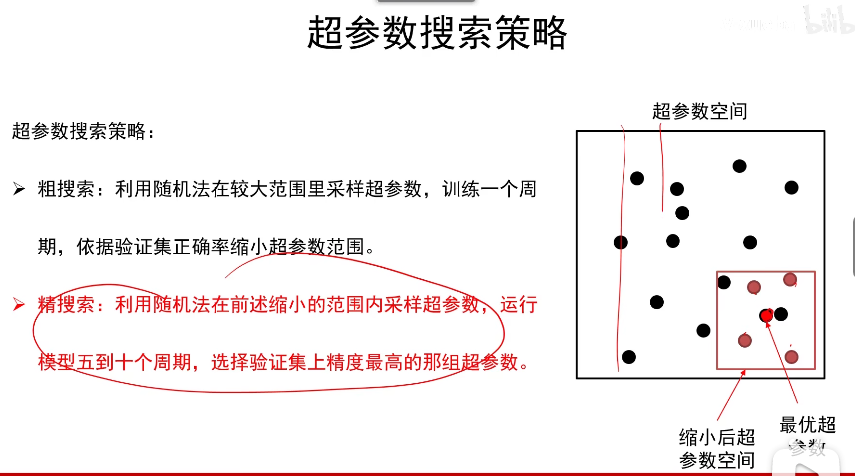
也就是说粗搜索搜索0-1的范围内随机采点,然后发现0-0.1范围内效果较好,那么我们再在0-0.1范围内随机选取几个点进行精搜索。

第一种情况显然选取0.1-1的概率较大,但是这些参数的数量级相同(都是0.1数量级的),因此结果差不多。
Softmax分类器
以上的方法的过程是这样的
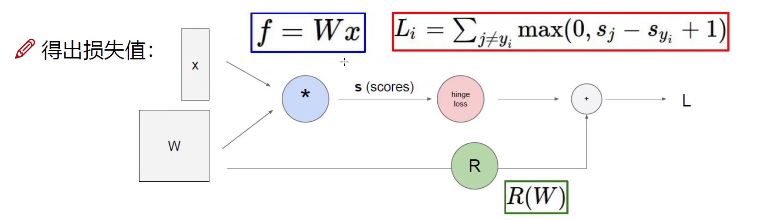
当中根本没有涉及到概率,因为分类任务通常要看属于某个类别的概率值,因此我们要将上面的模型做一些变化,首先来看softmax分类器

- exp是放大每个分数的差距的
- 归一化是将分数转换为概率的,它是指将每项的分数除以所有项的分数之和,得到这一项的概率
- 而计算损失值的时候是将输入的类别的概率带进去计算的,比如我输入的是一只猫,那么我就将0.13带进去,负号是因为概率是在0和1之间的,因此log为负数,加个负号我们将它转换成正数
- 注意这个log函数的损失叫做交叉熵损失
此时我们修改上面的模型:
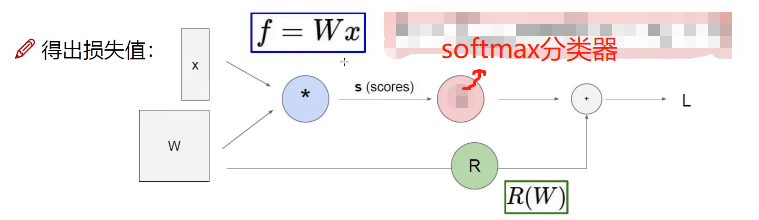
这个模型是分类任务的模型,而上面的模型是回归任务
前向传播与反向传播
前向传播将得分转换成概率而得到了一个损失值,而反向传播是更新w从而使得损失值达到最小
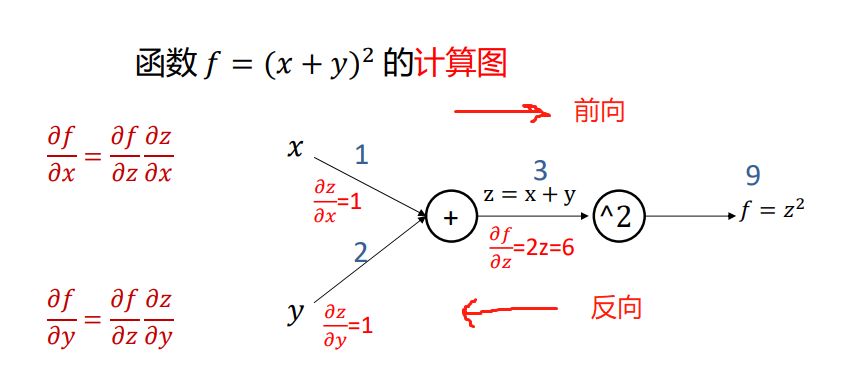
反向传播

以上图为例对线性分类器而言,W矩阵的第一行乘以xi做一次反向传播,W矩阵的第二行乘以xi做一次反向传播,W矩阵的第三行乘以xi做一次反向传播,当然此时所有的w和x都是未知量,它们可以组成一个多元函数。
反向传播的实质其实就是多元复合函数求偏导:
f(w,x)对w0求偏导:
分开求
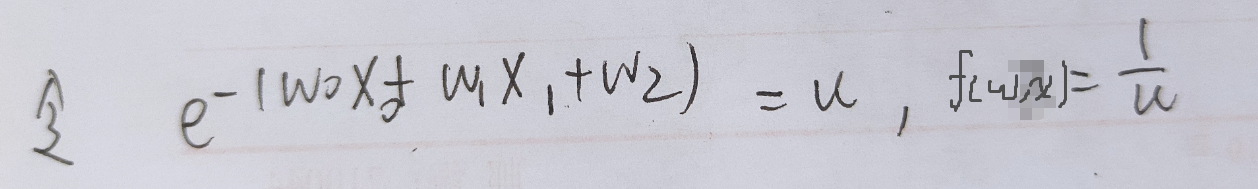
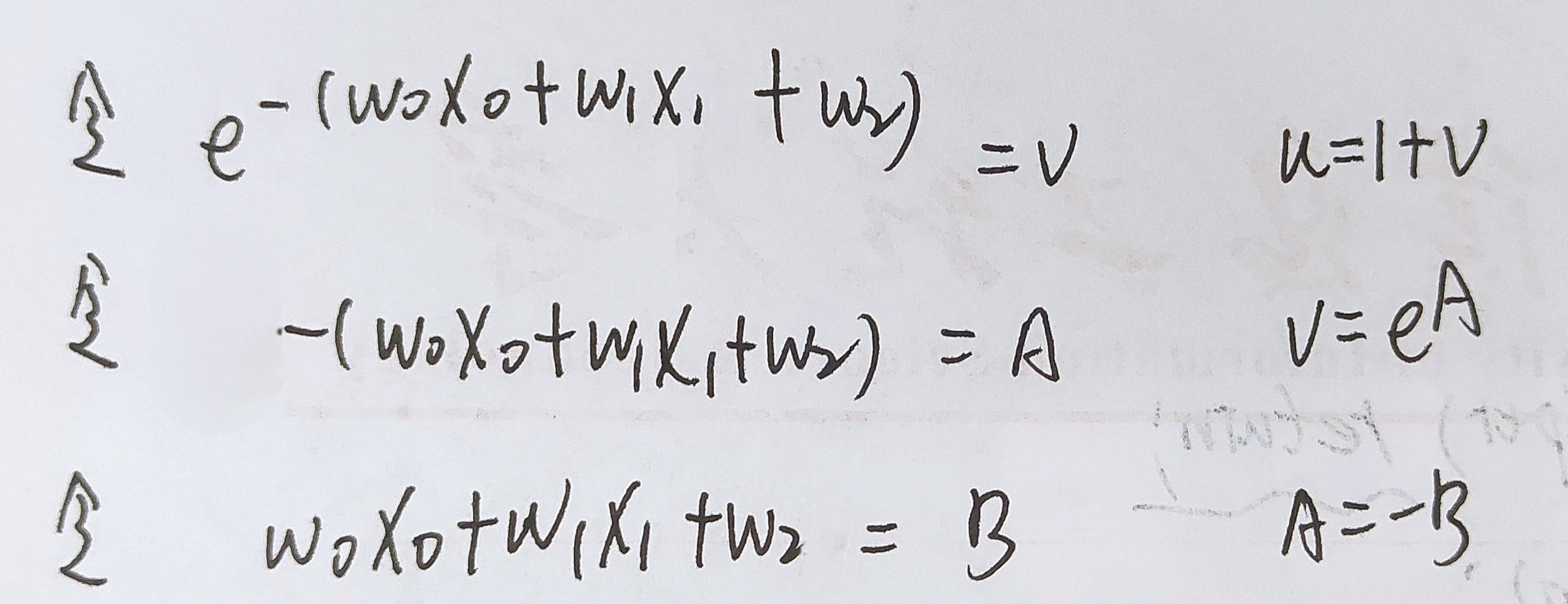
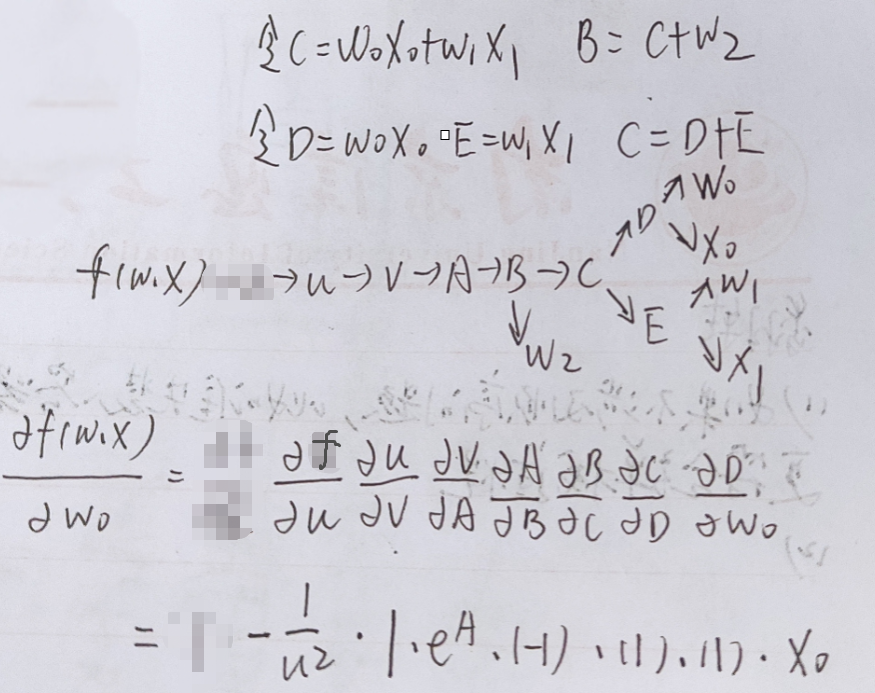
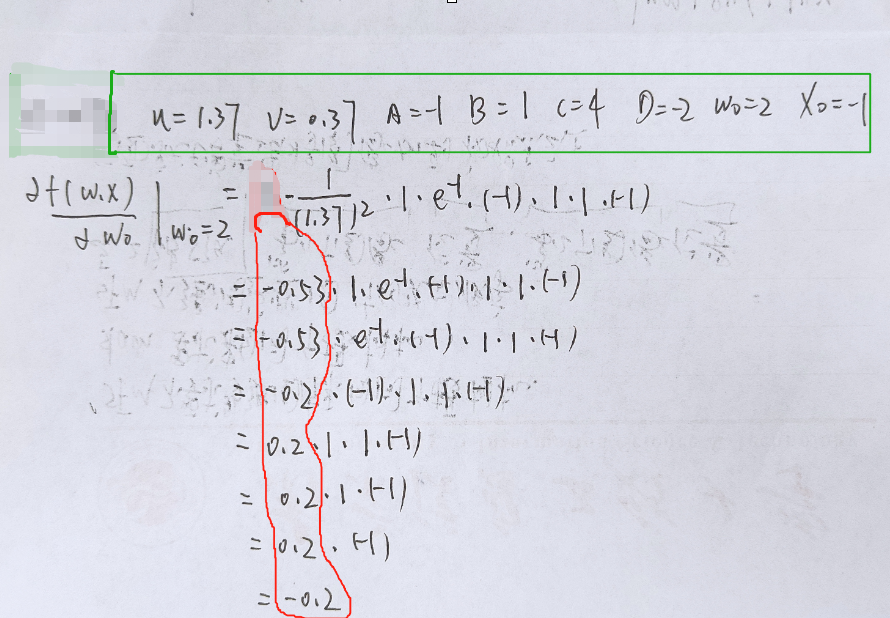
如果分开求的话,f(w,x)的输入是没有用的,要从1/u的地方算起
整体求:
该方法颗粒度比较大但是计算效率比较高
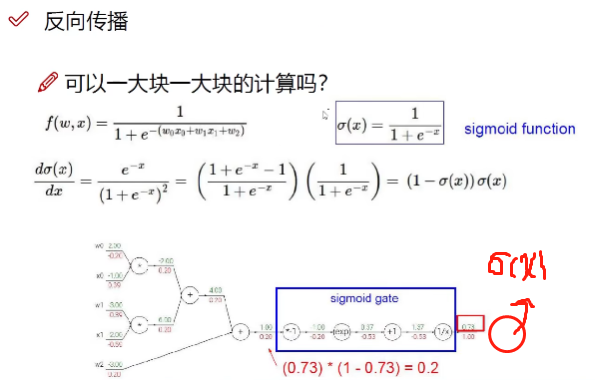
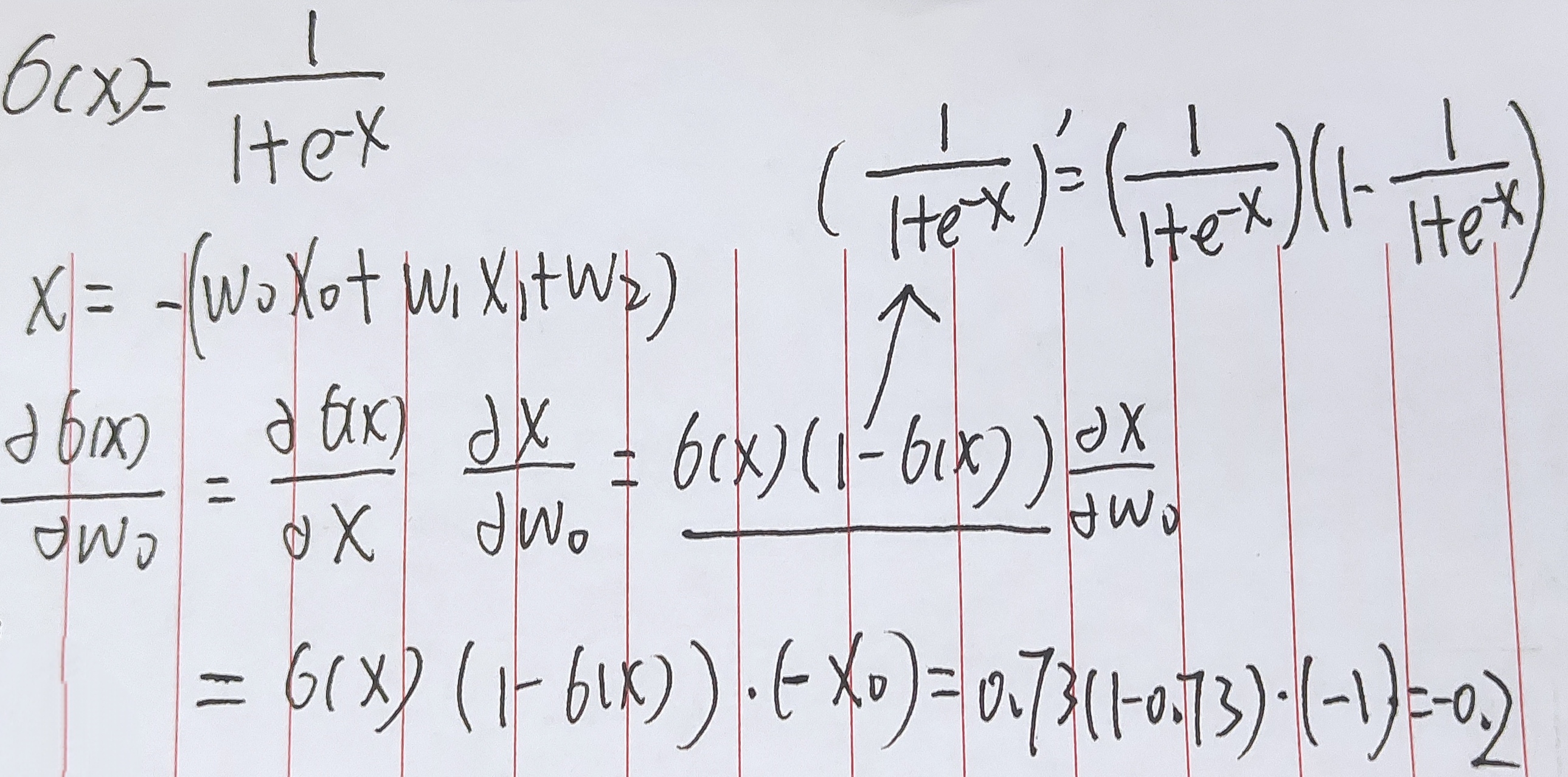
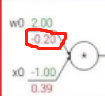
- 绿色就是反向传播那张图中绿字部分,也就是输入,红色是反向传播那张图中红字部分,也就是输出,注意上图中涉及到约等于
- 可以得出的规律是:上一次的输出(右边是左边的上一次)乘以本次的求导结果就是本次的输出
这是另外一个例子:
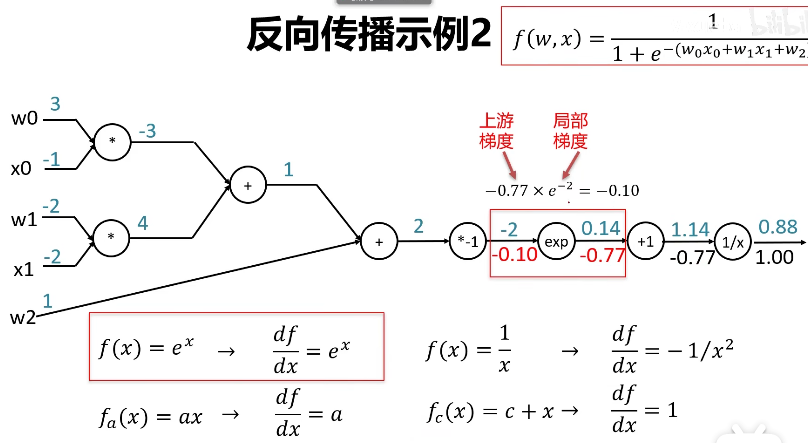
上述内容的作用
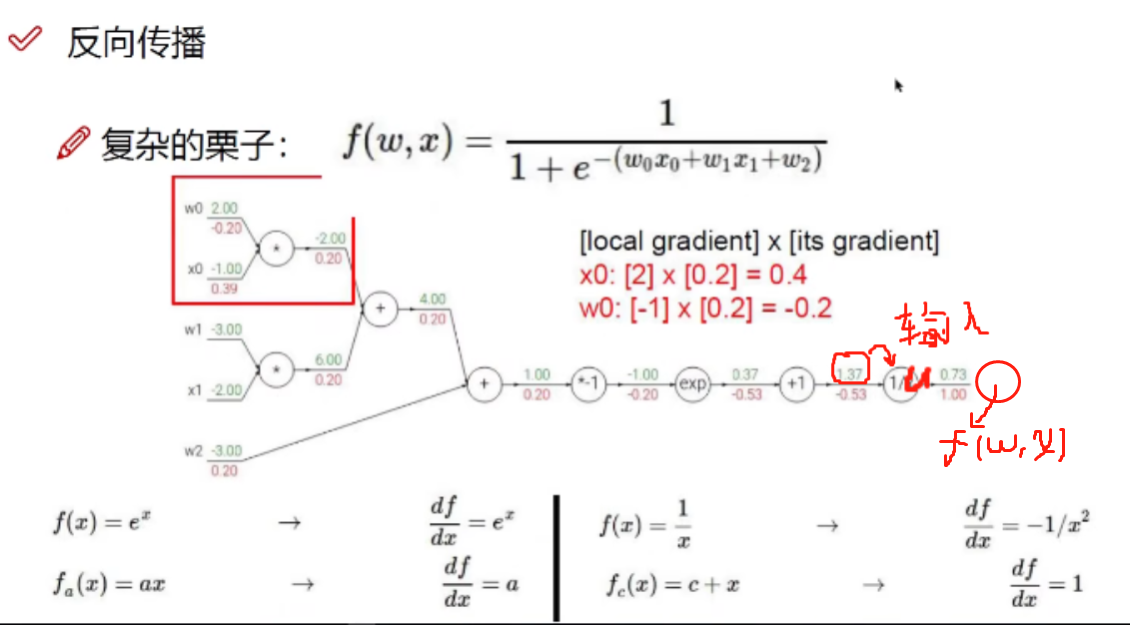
假定损失函数为L(Y),Y=(w0,w1,w2,x0,x1)T,我们求损失函数极小值的策略是:对L(Y)使用梯度下降:


注意真正的神经网络只更新权值,也就是只对权值求梯度,而特征值作为损失函数中的常数
门单元

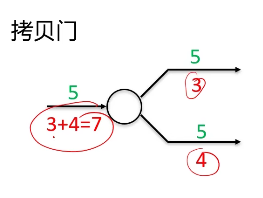
前向传播反向传播的具体例子
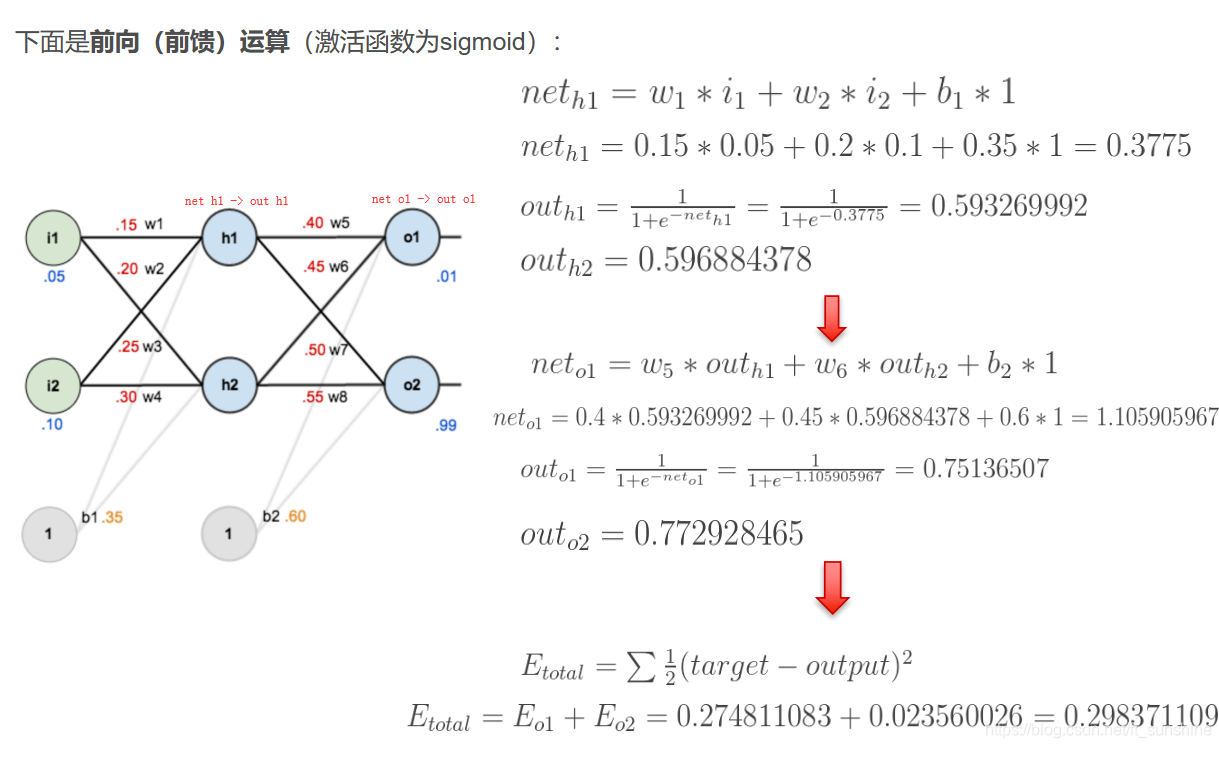
权重加权求和->加入激活函数->权重加权求和->加入激活函数.......

对每层表达式求偏导,然后带入这个偏导的变量中

上述的E就是损失函数
参考文章:
“反向传播算法”过程及公式推导(超直观好懂的Backpropagation)_aift的博客-CSDN博客
损失函数优化算法
梯度下降法(BGD)
注意我们的样本是图像

梯度下降的缺点
![]()
也就是验证分类器的图像过多,导致计算量过大,改进方法是随机梯度下降法
随机梯度下降法(SGD)
原来是使用所有的图像,每个图像去验证这个分类器就会产生一个损失,然后所有的损失加和再取个平均,就是总损失,然后对总损失求梯度,最后使用梯度下降法更新权值。但现在的策略是每次只拿出一张图像去验证这个分类器,然后求出损失,最后只拿这个损失计算梯度更新权值。

缺点:单个样本的训练可能会带来很多噪声,不是每次迭代都向着整体最优化方向,但是多次迭代,每次迭代都使用不同的图像就会使得多次迭代整体的迭代方向是朝着最优化方向。
小批量梯度下降法(MBGD)
每次随机使用m个图像,计算每个图像的损失,然后加和取平均,然后求梯度更新权值,这是一次迭代,然后再随机使用m个图像再完成上述过程,我们可以使用均匀抽样抽出m张图像,我们可以随机抽取m张图像,这就导致每次迭代所抽取的图像可能相互重复,并且有些图像没有参与迭代。

假定有N张图像,我取了N张图像完成多次迭代后就是一个epoch,当然有些图像可能没被用到
梯度下降存在的问题

梯度某一方向的分量使得损失函数沿该方向下降的很慢(也就是说每次的梯度方向都会朝这个方向但是梯度很小因此更新的很慢),梯度的另外一个分量使得损失函数沿该方向反复振荡(反复振荡的含义就是相邻的梯度方向可能不同,这就会导致梯度方向一会朝这一会朝那,从而该权值的更新方向一会朝这一会朝那,在极小值点周围反复振荡),致使收敛速度较慢,而增大步长只会增大振荡方向的振荡幅度。
改进方法:
动量法(Momentum)

v=μv+g:
v(k+1)=μv(k)+g(k+1)
v(k+2)=μv(k+1)+g(k+2)=μ(μv(k)+g(k+1))+g(k+2)
这说明本次的v累加着它之前的所有的历史梯度信息:


μ取0.9会使得历史梯度逐渐衰减,当本次梯度,历史梯度为0,那么权值θ就不再更新,如果μ为1那么历史梯度不会衰减,则权值θ会一直更新下去。μ为0就退化成MBGD
某点左右两侧的导数符号不同该点称为极点,导数符号相同该点称为鞍点。

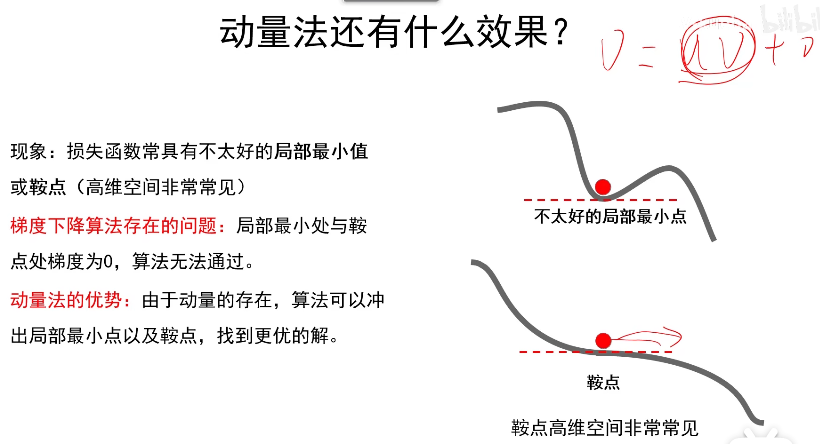
梯度下降法当梯度为很小的时候就停止更新,假定梯度为0的时候停止更新,这样会使得损失函数在局部最小点或则鞍点停止,但是动量法当梯度为0的时候也就是损失函数处于局部极小点或则鞍点的时候由于μv不为0,因此不会停止更新,这就会使得损失函数冲出极小值点或则鞍点。
自适应梯度法(AdaGrad)

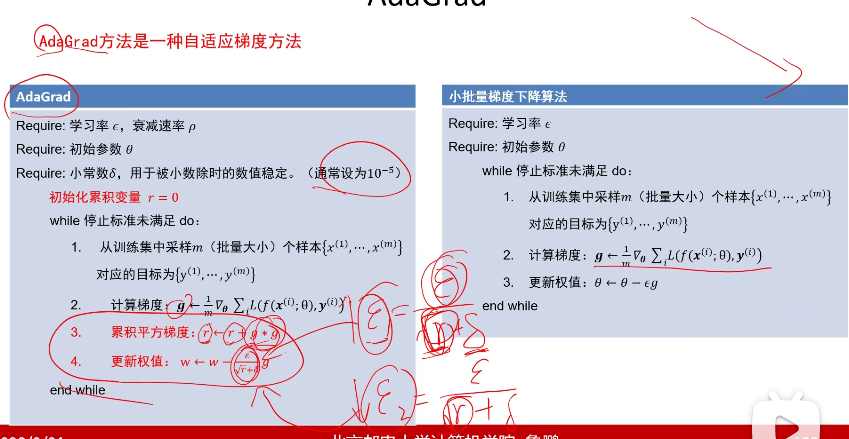

从上面可知,振荡方向学习率较小,平坦方向学习率较大,δ是超参数不重要只是用来保证分母不为0。
上述方法的问题是,随着累积的次数增多,r会越来越大,导致最后平坦方向的学习率和振荡方向的学习率都很小,这就失去了算法的作用。
改进方法:
RMSProp

ρ=0仅考虑当前梯度,当前梯度较大则对应的学习率就会较小(不大清楚为什么ρ=0不行),难道是ρ=0后的√r会等于g,这样就区分不了振荡还是平缓?(振荡和平缓要靠g2区分)
ρ=1就退化成BGD了

Adam

冷启动:开始的学习率和v都很小,上例显示修正偏差后开始的v等于梯度,当随着迭代次数的增加,v(~),r(~)逐渐接近v和r,从而发挥作用
深度学习的整体架构(全连接神经网络为例)
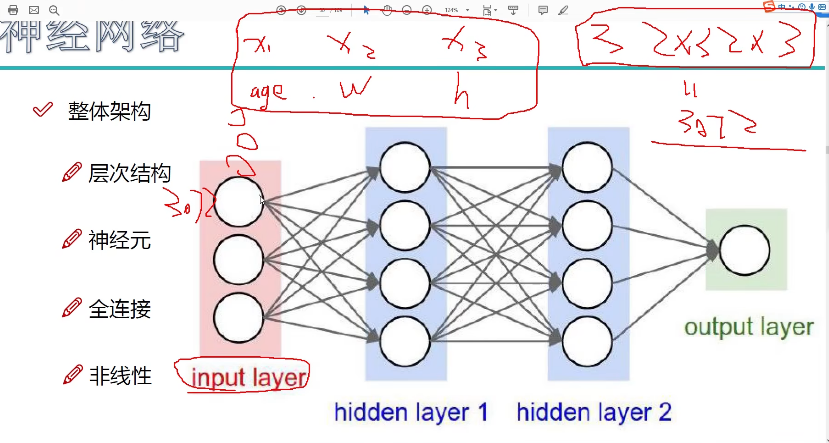
有多少特征,input layer有少个圆圈,比如一个32*32*3的图像就有3072个特征,那么就有3072个圆圈,32*32*3如果看成一张小猫的图像的话,也就是用3072个特征代表一个小猫,权重代表小猫这张图像哪些特征重要哪些特征不重要,如果得到了一个合理的权重,那么我们可以根据这个权重来判断这个物体是什么,如果小猫1特征重要权重比较大,2特征重要权重比较大,3特征不重要权重比较小......3072这个特征不重要权重比较小,那么下次我们拿来一个1的权重比较大,2的权重比较大,3的权重比较小......3072权重比较小的w向量,就可以判定这个物体是只猫

全连接神经网路可以看作多个线性分类器通过非线性变换后的级联的结果
层数的定义
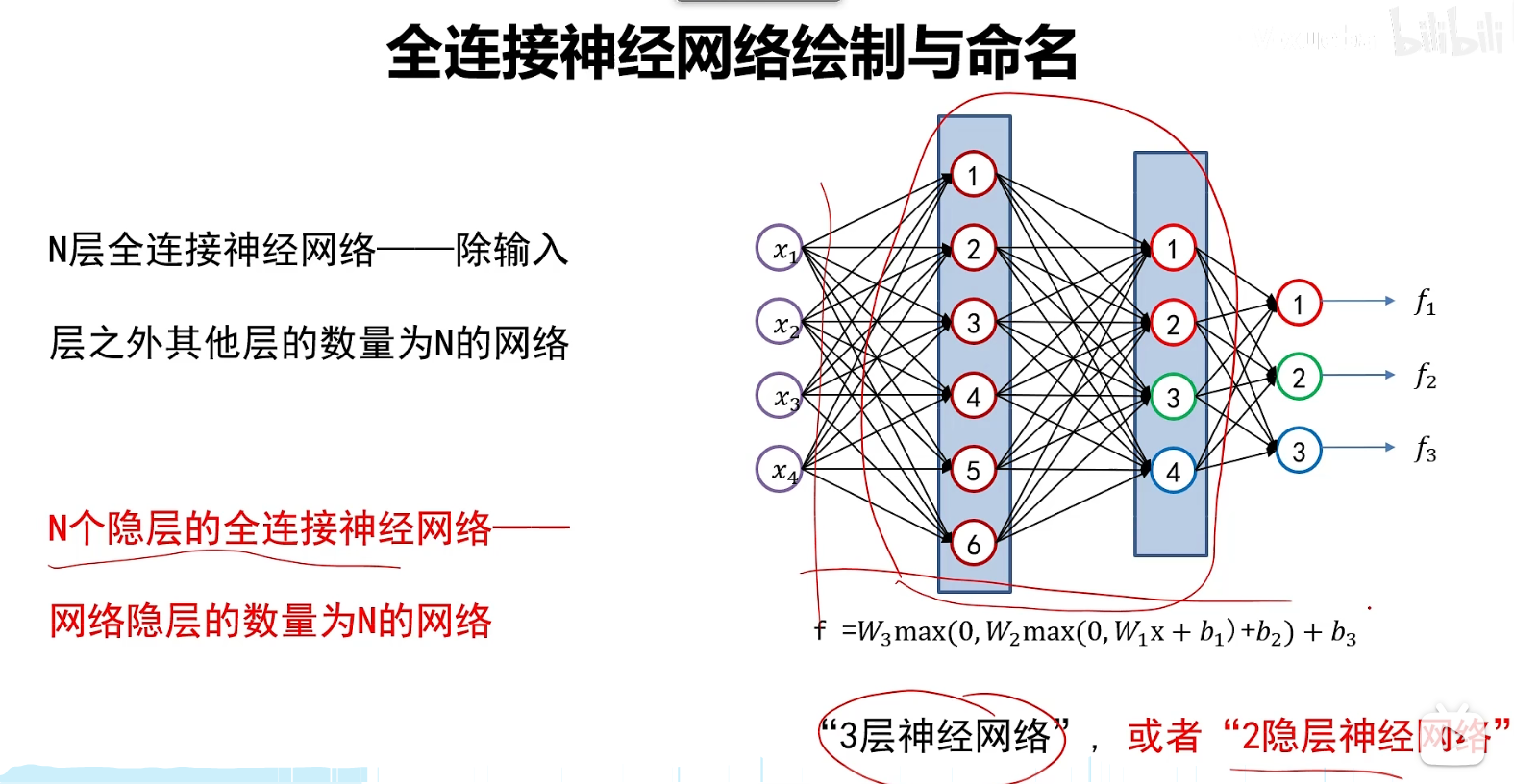
全连接:
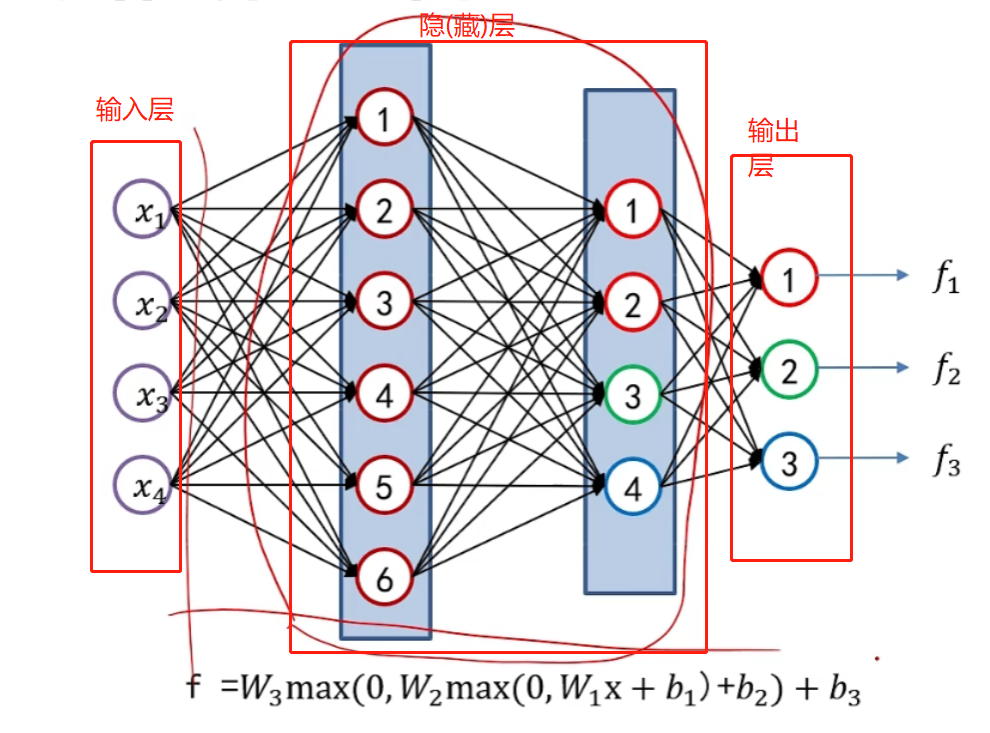
A和1,2,3,4都相连;B和1,2,3,4都相连;C和1,2,3,4都相连
- 输入层先进行预处理然后输入,输入层的神经元个数是特征数
- 隐藏层每次经过线性变换形成多维向量后使用激活函数进行处理,隐层的神经元个数是可以自由设置的
- 最后的隐藏函数的输出作为输出层,输出层的神经元个数是类别数
非线性
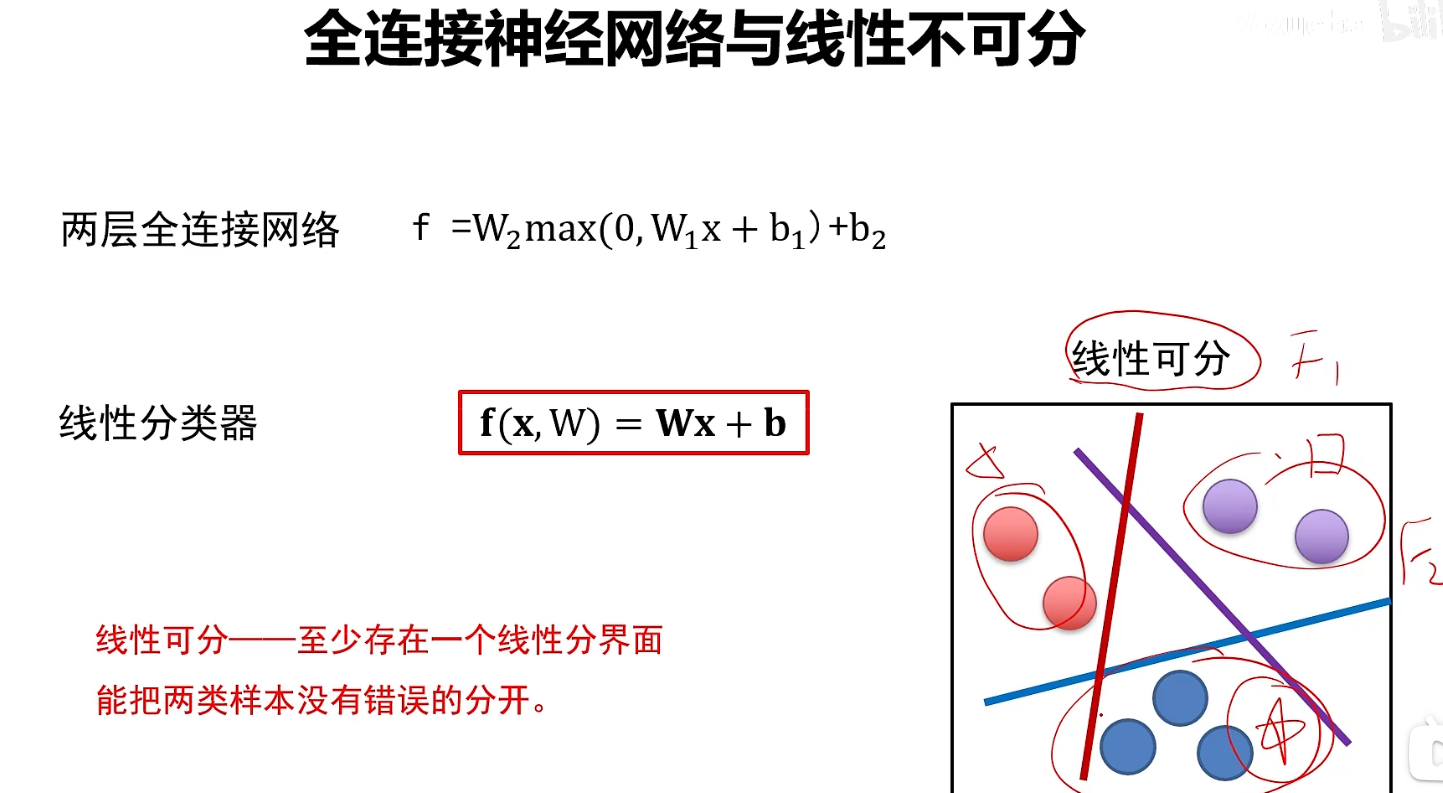
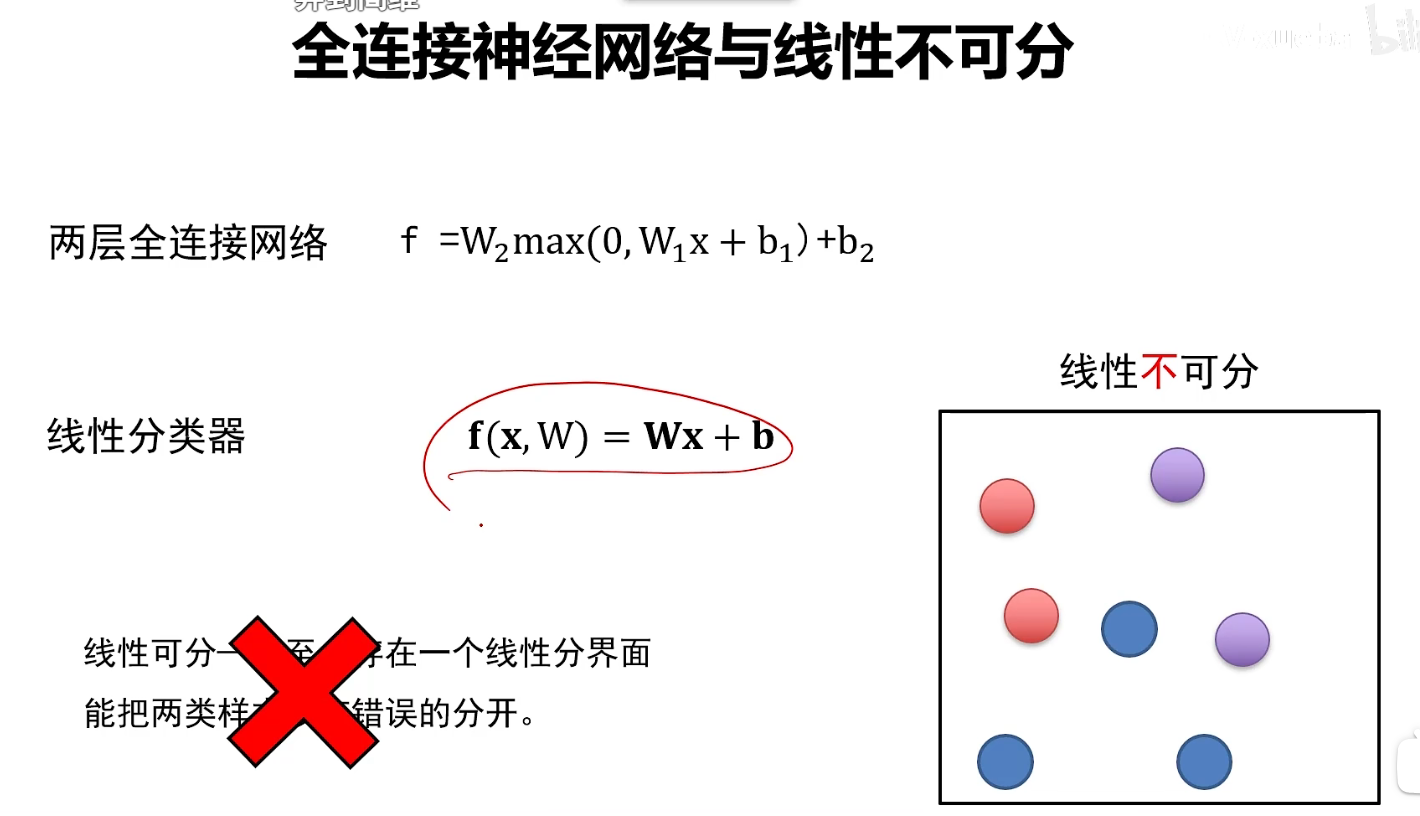
非线性指的是指激活函数是非线性的,线性分类器是解决不了这种线性不可分的问题的,因此我们使用这种非线性函数来解决线性不可分的问题
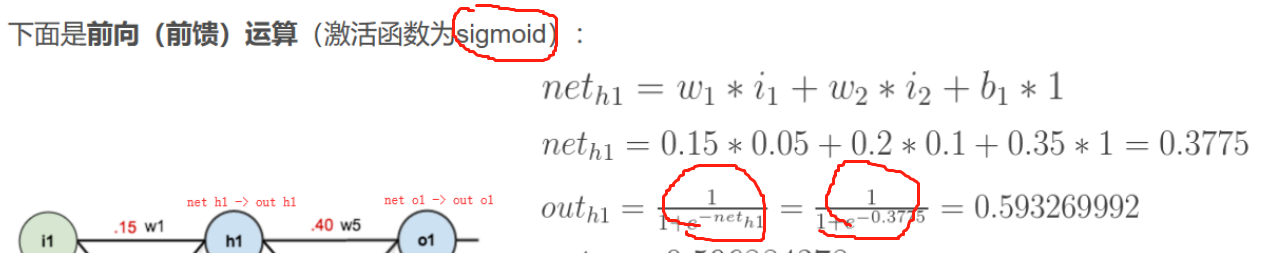
也可以是max函数

激活函数
激活函数是对前一层的输出分别进行处理,也就是将每一个得分值带入作为激活函数的自变量值,得到的因变量值作为下一层的输入

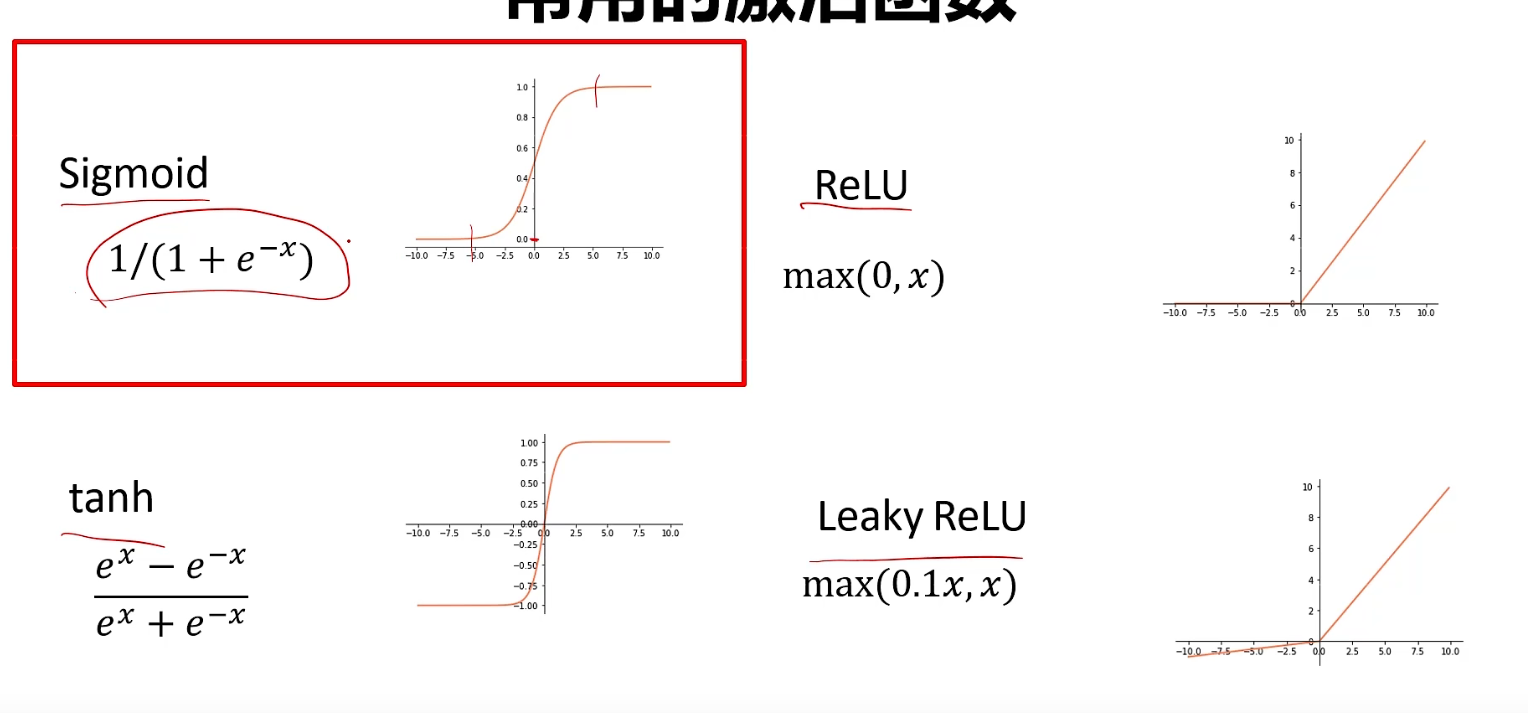
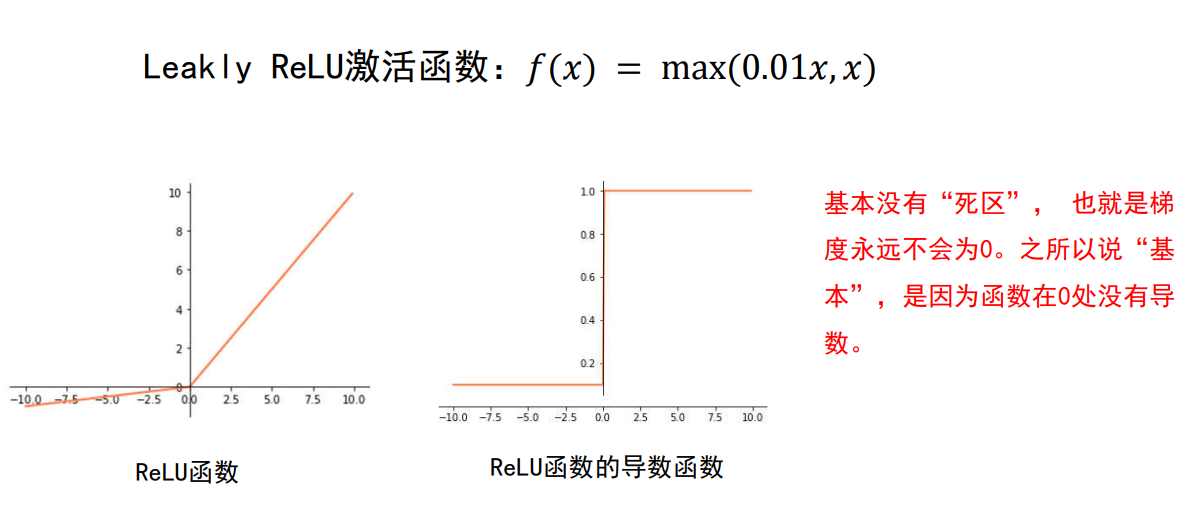
sigmoid函数缺点:当输入过小或则过大都会使梯度为0,这就是所谓的梯度消失,因此sigmoid函数基本不用了,但是可以在输出层使用,使输出在0和1之间,中间的所有隐层就不再用了,我们现在常用的是Relu函数,即输入和0进行比较,小于0就输出为0,大于0就输出输入的值,或则使用leaky Relu。

梯度消失
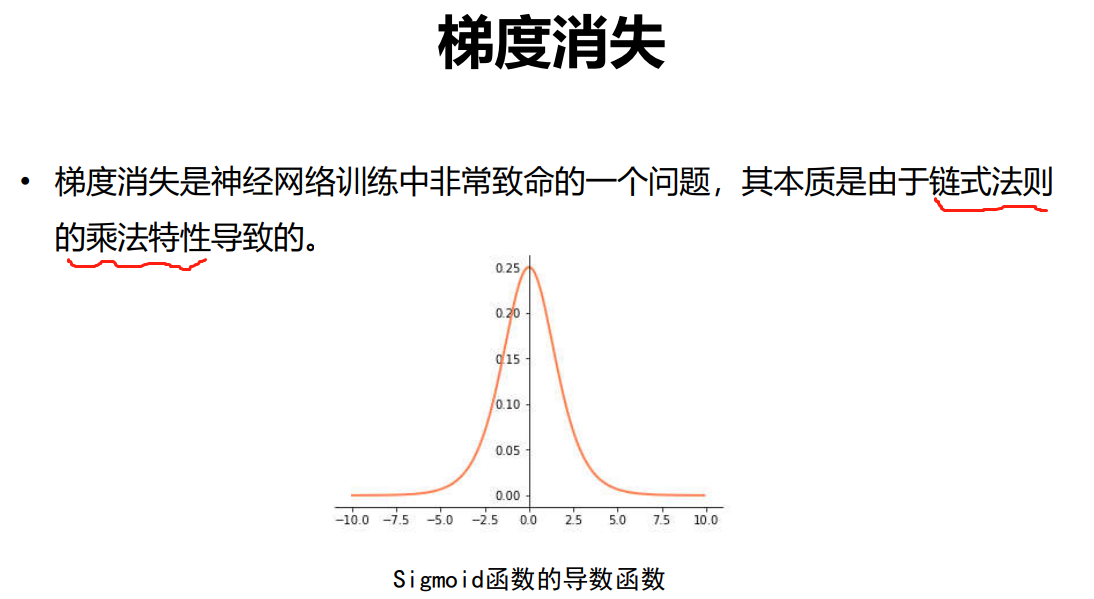

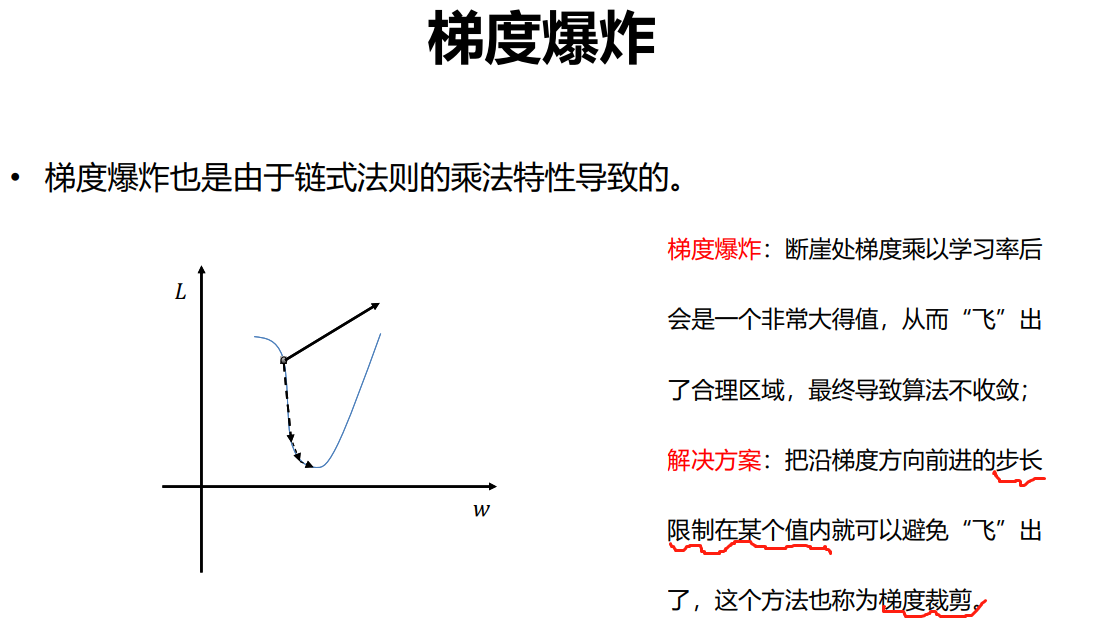
梯度爆炸

神经元的个数对结果的影响
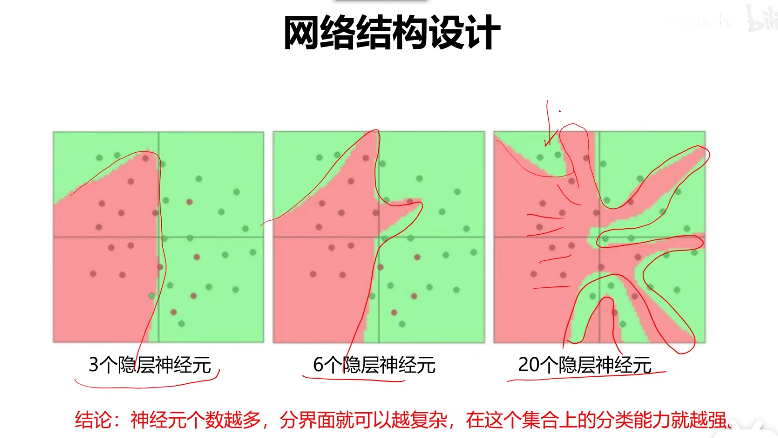

神经网络的设计要素
宽度,深度,激活函数的选取

宽度和深度越大模型越复杂,非线性更强一些,但是增加深度有效性好一些
SoftMax分类器
没有softmax分类器时:
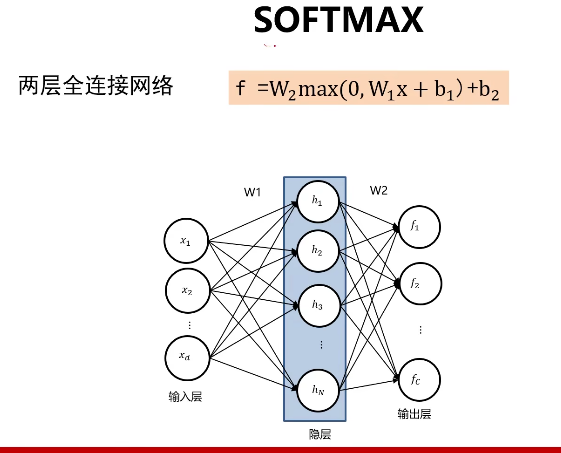
有softmax分类器时:

该输出层表示属于这一类别的概率

交叉熵损失
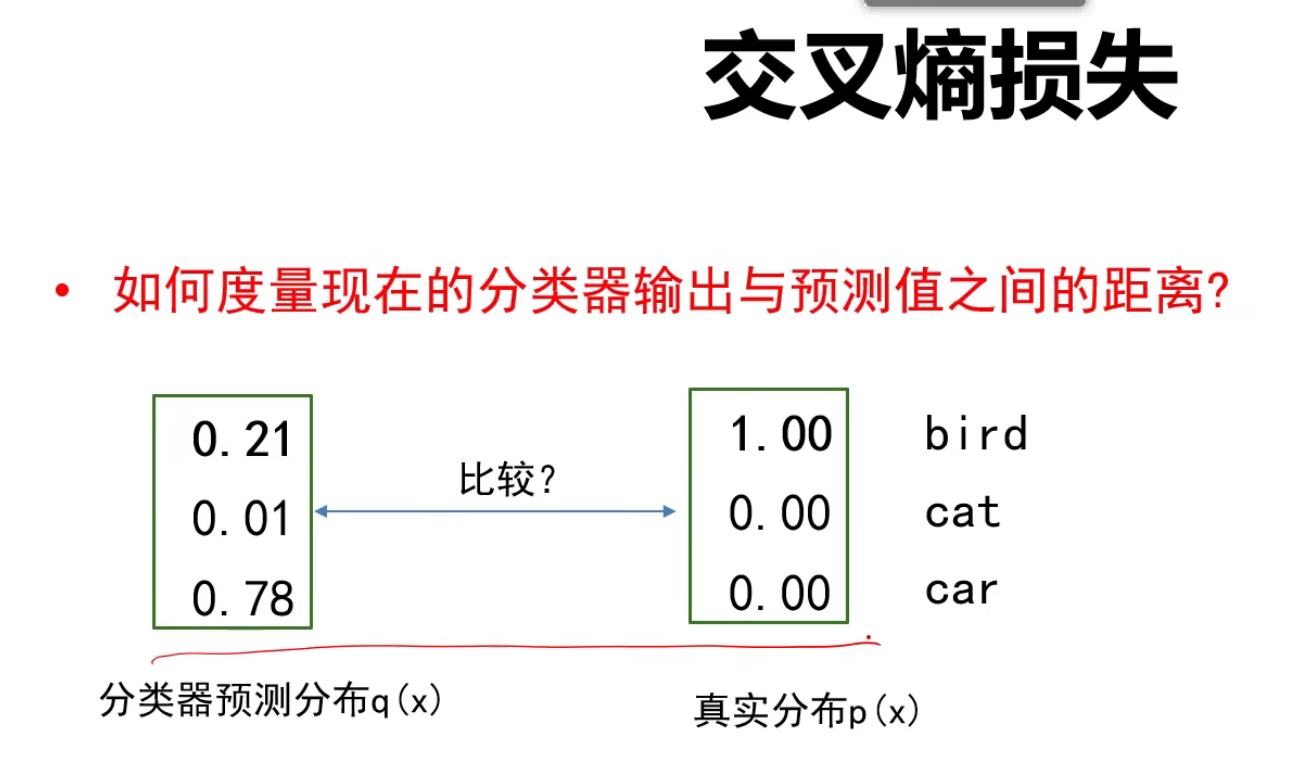

其实我们要求的是相对熵(KL散度)这种情况下交叉熵和相对熵相等,也可以度量两个分布之间的不相似性
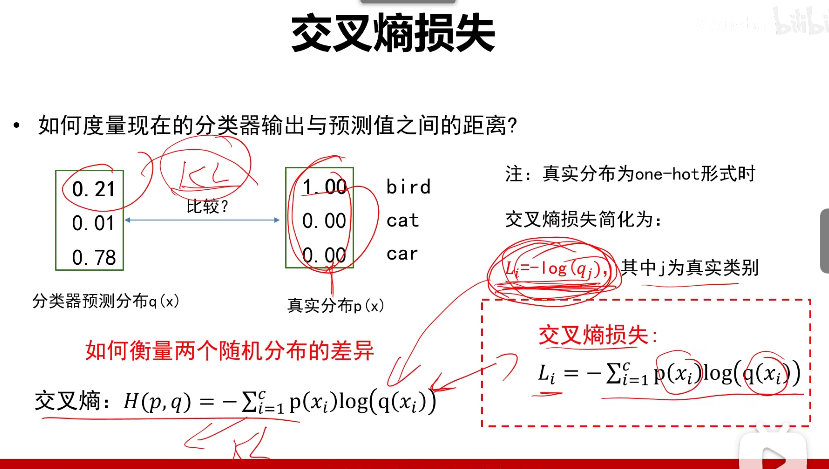
交叉熵损失和多类支持向量机

如上图所示,第二行虽然10胜出了但是10这个类别和其他类别都很接近所以依然有很大的损失
使用交叉熵损失可能会出现如下的情况:

第一次预测是错误的,第二次预测是正确的,虽然精度有很大的提升但是交叉熵损失却没什么变化,而且有很大的损失,这表明交叉熵损失不允许各个概率都比较接近,它要求输入的那个类别的预测概率要远大于其他概率




 浙公网安备 33010602011771号
浙公网安备 33010602011771号