非线性优化理论（求极小值）

极值点存在条件：

 

方向导数与梯度：

梯度的求解方法

 

技巧是：

梯度下降法

迭代条件：

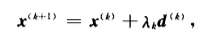
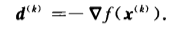
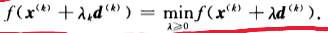
向量A和向量-A方向相反，夹角是180度。e_l=-▽f(x^(k))

 

注意如果x_k,x_k+1,梯度是向量的话，那么就变成了向量的加法，不再只是一元的沿着x轴更新

 

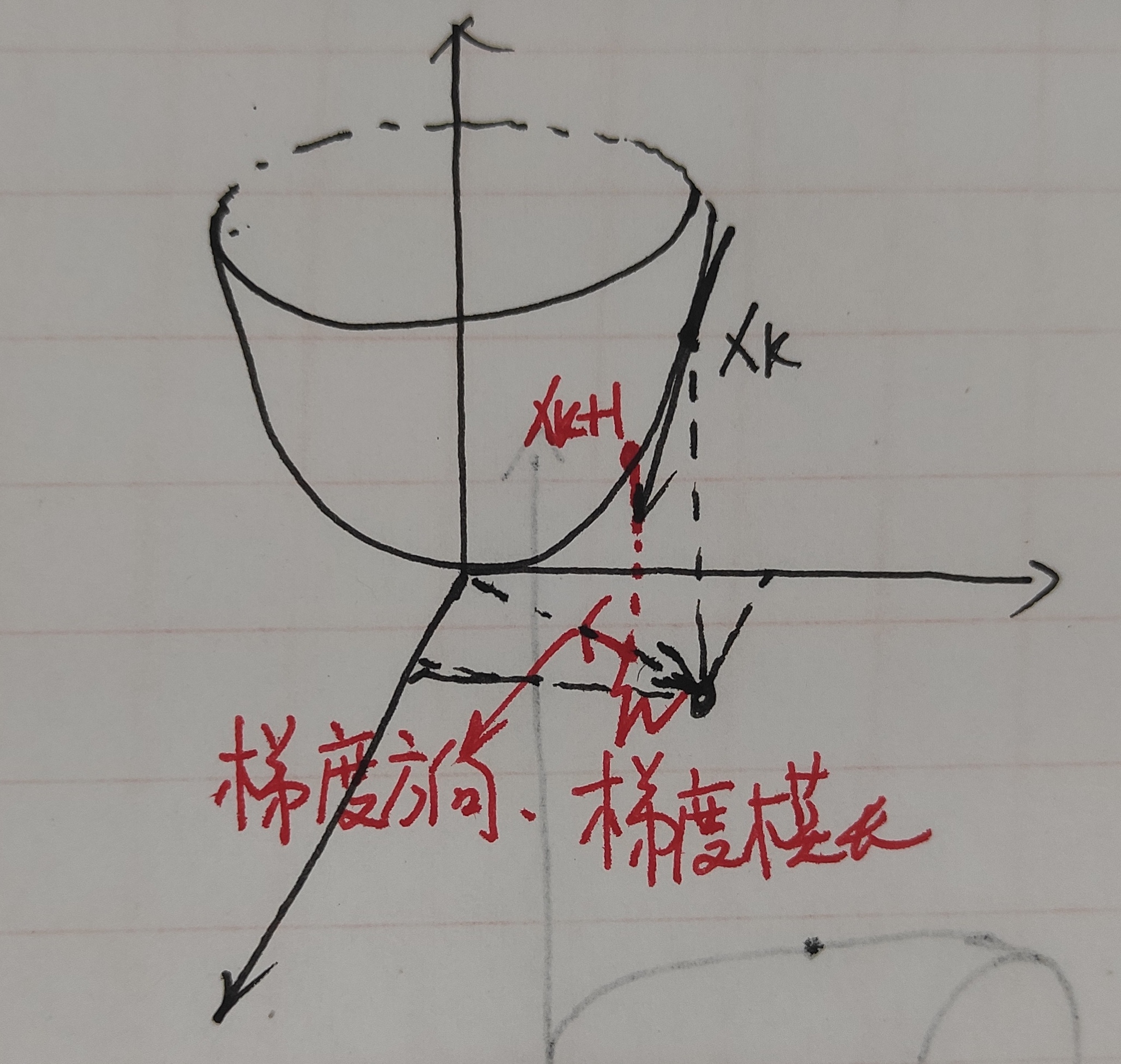
梯度下降法的缺点：

• 初值的选择可能是结果掉入局部最优。
• 步长过小可能要好多步才能到达极小值，收敛速度较慢。

    

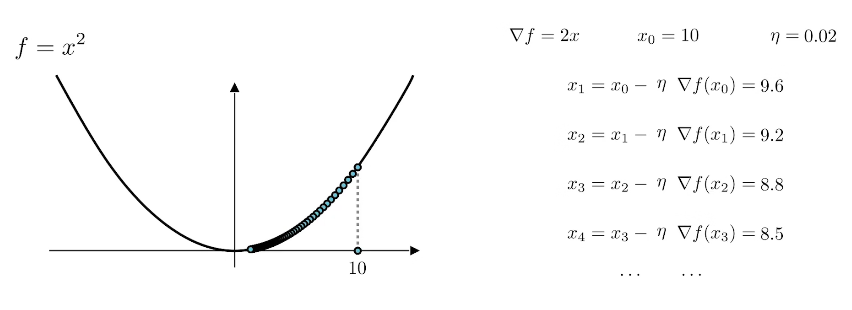
另外当靠近极小值的时候，图像都是很平缓的，因此梯度较小，因此△x就相对之前有所减小，因此越靠近极小值下降得越慢，影响收敛速度。

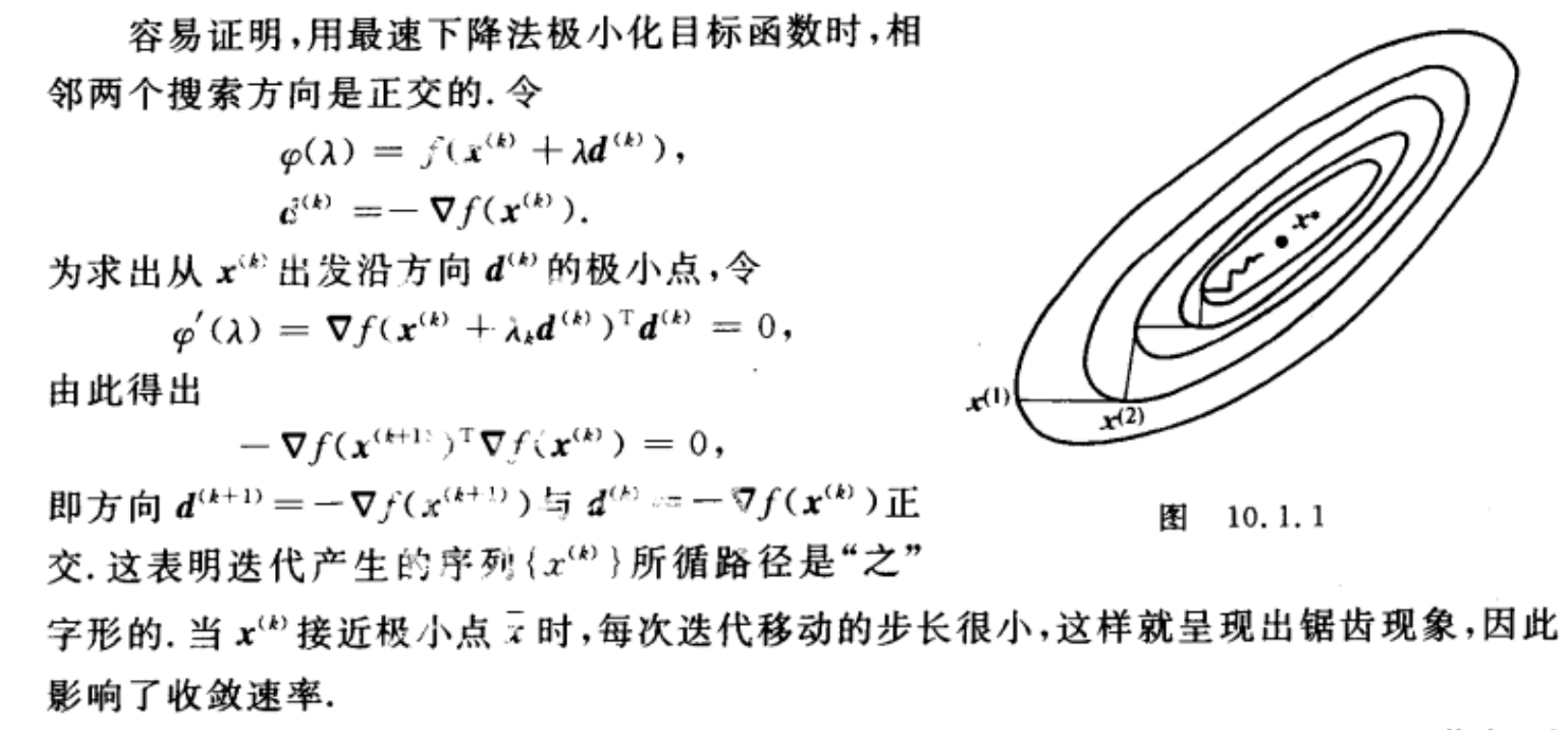
而且相邻的两个搜索方向是正交的，因此整体的路径成Z字形，这也影响了收敛速度。

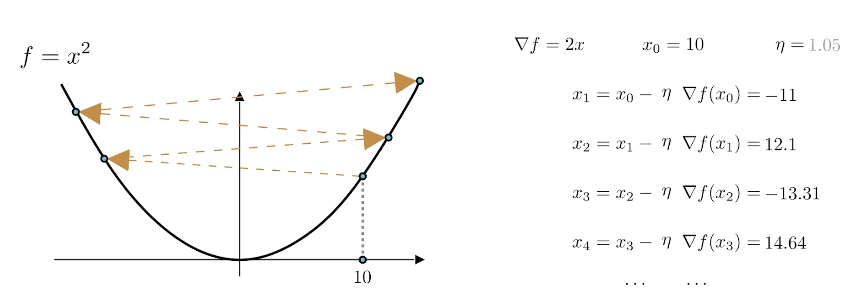
• 步长过大或则算法多次迭代后，可能导致在极值点周围的两个值之间反复振荡，收敛速度较慢

　　在极值点周围反复振荡：

           

　　 更新后的值反而增大：

       

可以迭代的前期使用梯度下降法

 

牛顿法　　

迭代条件

终止条件

根据极小值存在的充要性可知，海森矩阵是正定的，因此特征值都大于零，因此是可逆的，此外海森矩阵是正定的也保证了极小值的存在。

 

如果a,b,c都大于0说明正定矩阵不影响最后梯度的符号。

 

从上式可知牛顿法相对于梯度下降法，除了步长为1，还多了一个海森矩阵，当接近极小值时图像比较平缓，因此梯度变化比较小，海森矩阵比较小(一阶导数变化率小，二阶导数较小),因此海森矩阵的逆比较大，因此在图像比较平缓的极小值附近函数变化较大，收敛较快。

根据二阶导数的定义可知：

 

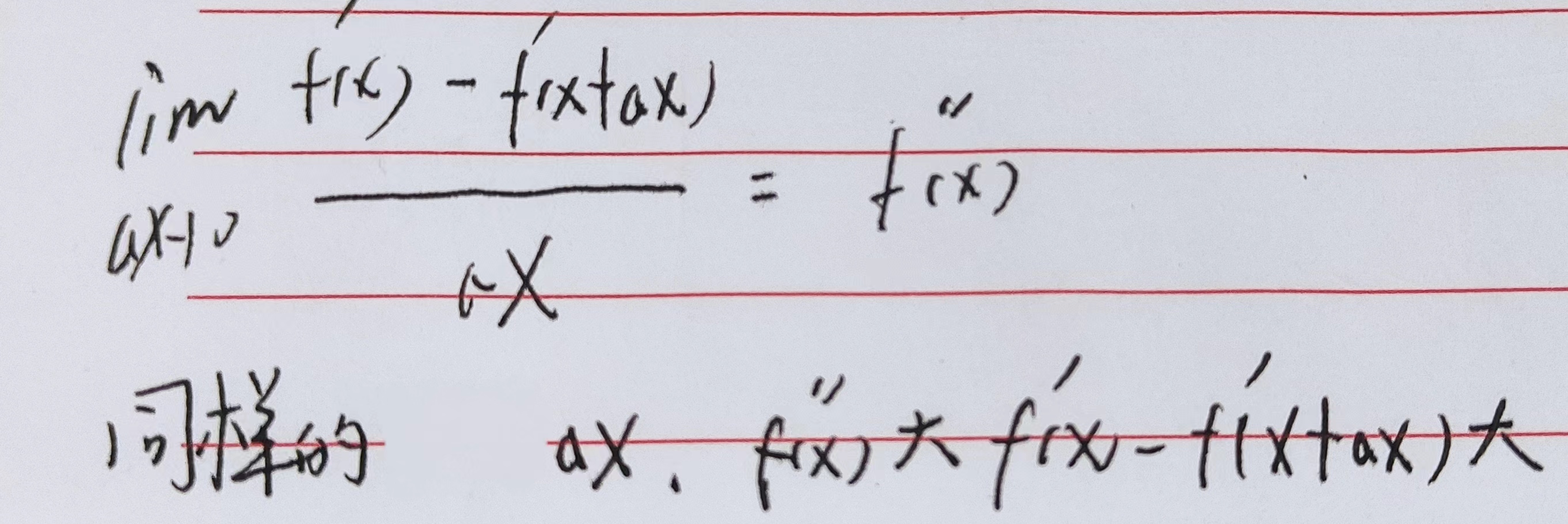
因此x变化相同的时候一阶导数变化比较大此时二阶导数比较大，一阶导数变化比较大在牛顿法中意味着一阶导数很可能在x变化较小的情况下就有很大的变化甚至可能变化到导函数为0的地方，也就是极值的地方，此时稍微增大步长就有可能跨过极值点，因此牛顿法使得一阶导数变化大的地方二阶导数也就是海森矩阵比较大，求逆就比较小，x变化的就比较小，不容易跨过极值点。

 

证明:

我们的目标是找到最小的f(x+Δx)

                                                  

 

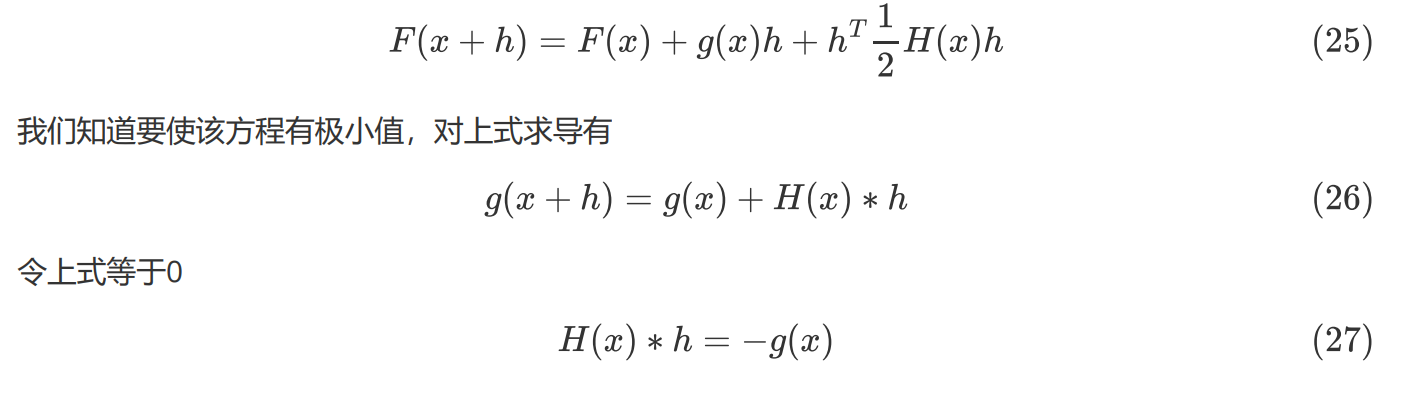
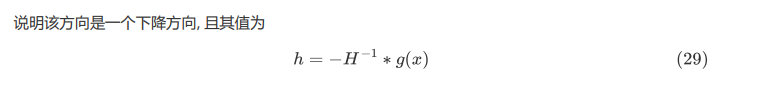
牛顿法的缺点:海森矩阵求解过于复杂计算量较大。

 

为了解决海森矩阵计算较为复杂的问题采用高斯牛顿法：

高斯牛顿法

迭代条件

 

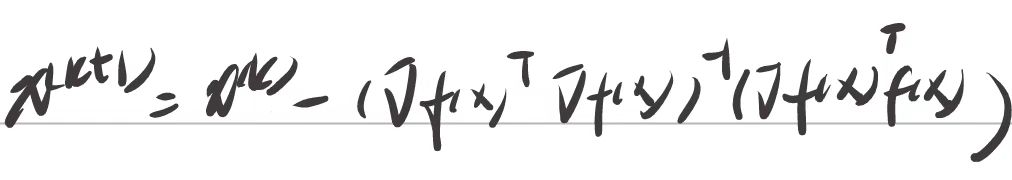
终止条件：

 

其实个人认为如果梯度足够小也可以认为是终止条件，因为在梯度足够小，接近于0时就基本接近了极值点。

 

首先明确：

 

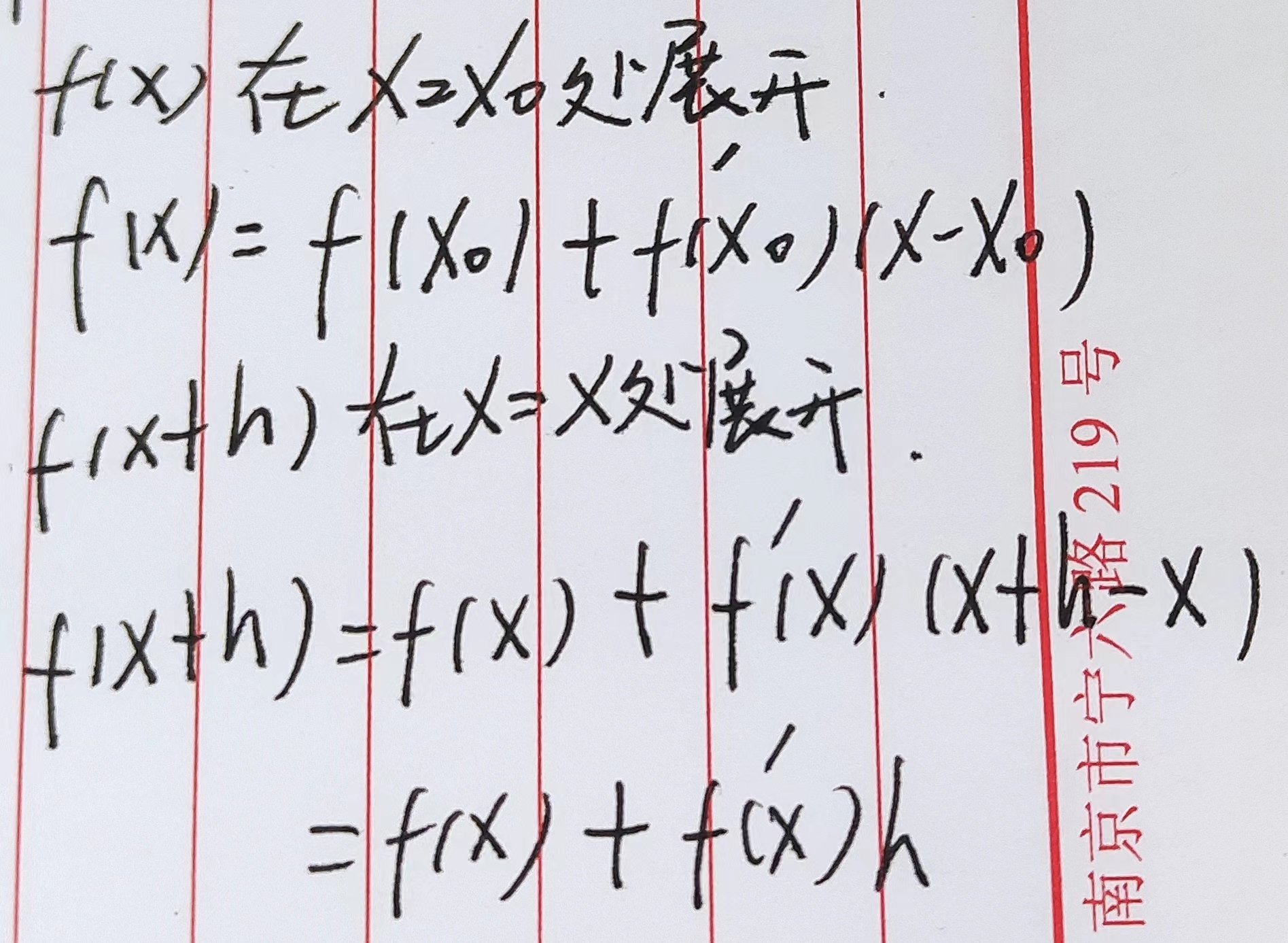
接着我们来看高斯牛顿法的推导：

注意这个地方f(x)是向量。

根据上式可得：

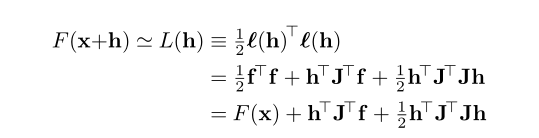
其中J是雅可比矩阵。

 

为解决上述问题采用LM算法

LM算法

 论文原文：