Games101学习记录（一）

前置知识

必备基础知识

基础数学
线性代数（重点是向量的运算，矩阵的操作）、微积分、统计。

基础物理
光学、力学

以及，信号处理、数值分析、以及一点点美学

在图形学中如果没有特殊说明，一般默认表示向量是列向量

向量的点乘

（注：在这里粗体表示向量）

a·b = |a||b|cosθ

满足交换律、结合律、分配律

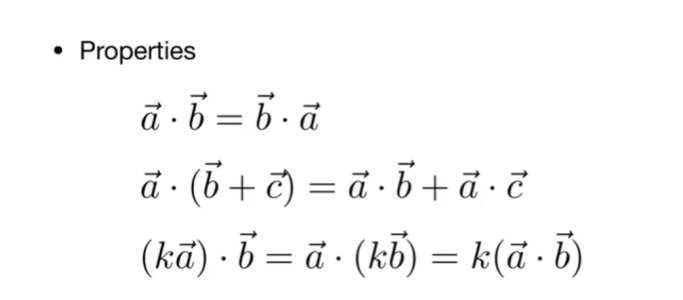
在坐标系下的运算

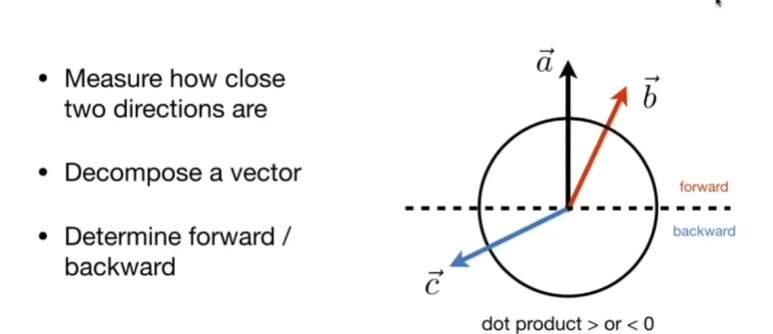
向量的点乘可以判断位置的前后

如果物体位置与比较位置为b，比较位置的方向向量为a，可以通过a·b的值来判断，物体在比较位置的前或者后

向量的差积

a × b = -b × a

|a × b| = |a||b|sinθ

a × a = 0

同样向量的叉乘满足分配律和结合律

叉乘可以判断左右和内外（左右：a × b > 0, b 在 a 的左边，内外:AP × AB,BP × BC,CP × CA的符号相同，则在三角形里边，反之则在外边。

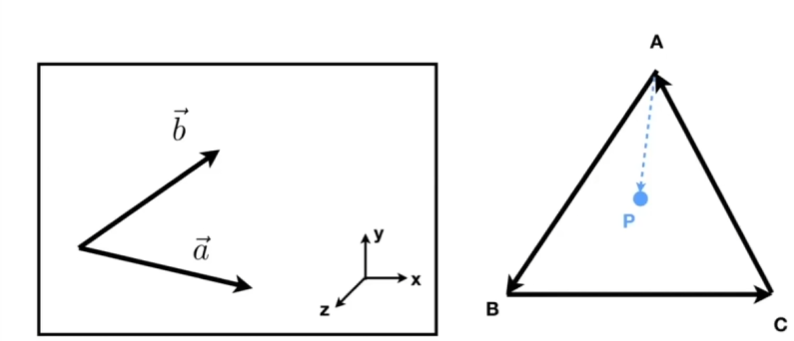
3维向量用方向向量表示

u v w为直角坐标系的3个方向向量

矩阵

矩阵的乘积

第一个矩阵的列数必须等于后一个矩阵的行数才能相乘

矩阵的乘积，没有任何交换律，有结合律和分配律

矩阵的转置

行和列调换

矩阵的逆

当两个矩阵相乘时，最后得到一个单位矩阵，则称这两个矩阵互为对方的逆

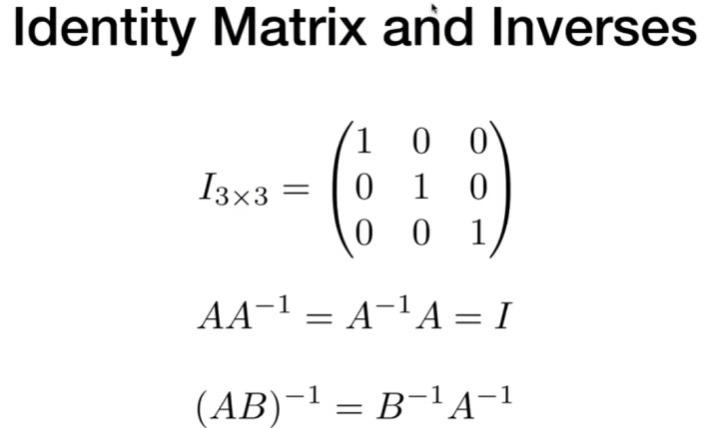
用矩阵表示向量的乘法

两个向量的点乘可以表示为前一个向量的矩阵的转置乘以后一个向量的矩阵

连个向量的叉称可以表示为 a 向量经过一系列变换为 A* 矩阵乘以 b 向量的矩阵

变换

二维变换

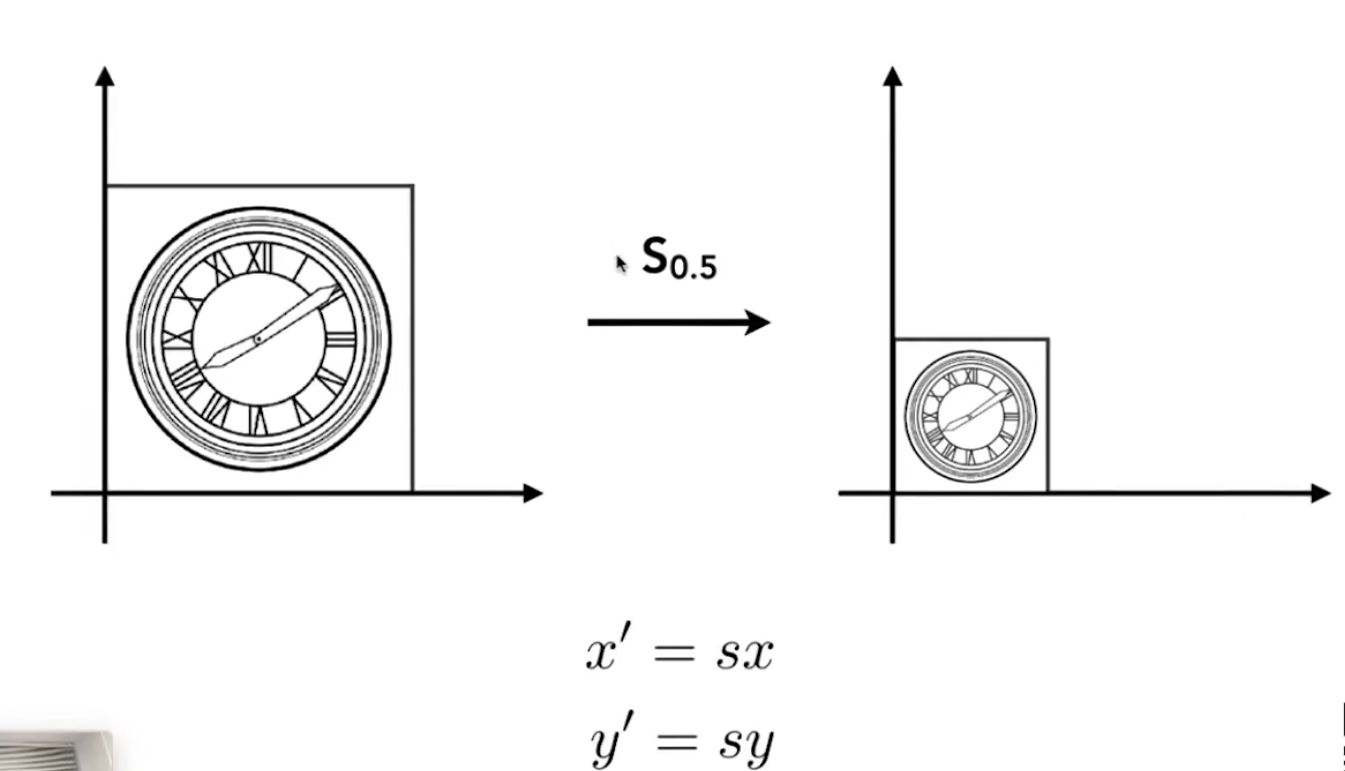
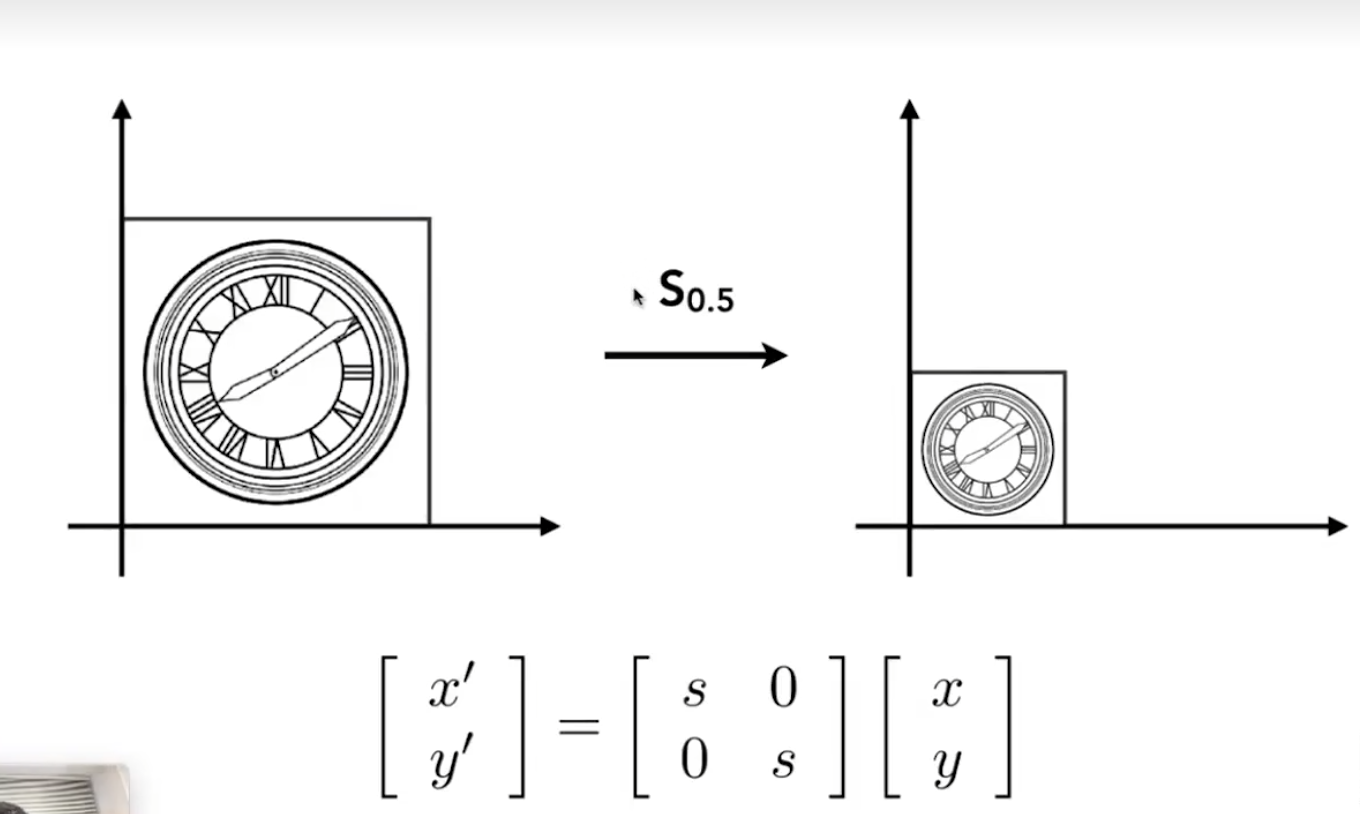
均匀缩放

非均匀

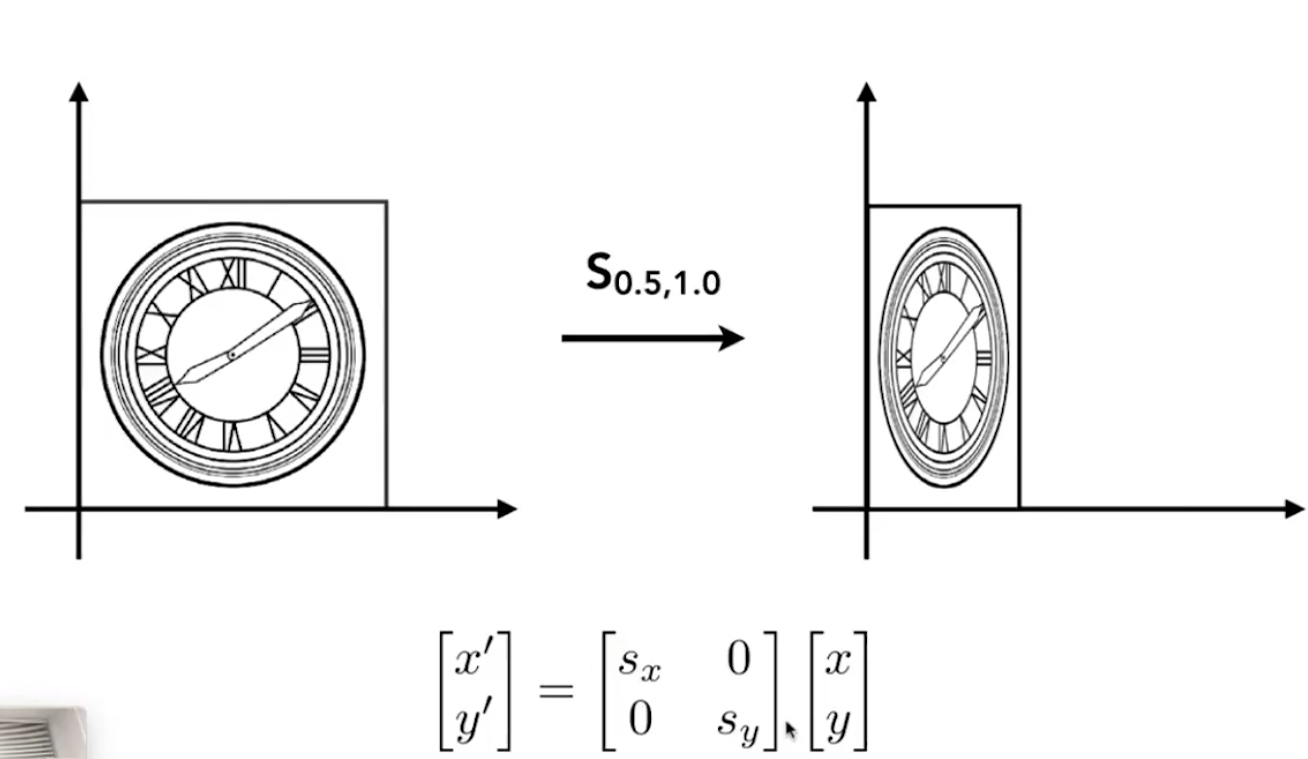
图中的S代表缩放系数，大于1时为放大，小雨1时为缩小，控制缩放的举证我们叫做缩放矩阵

镜像操作

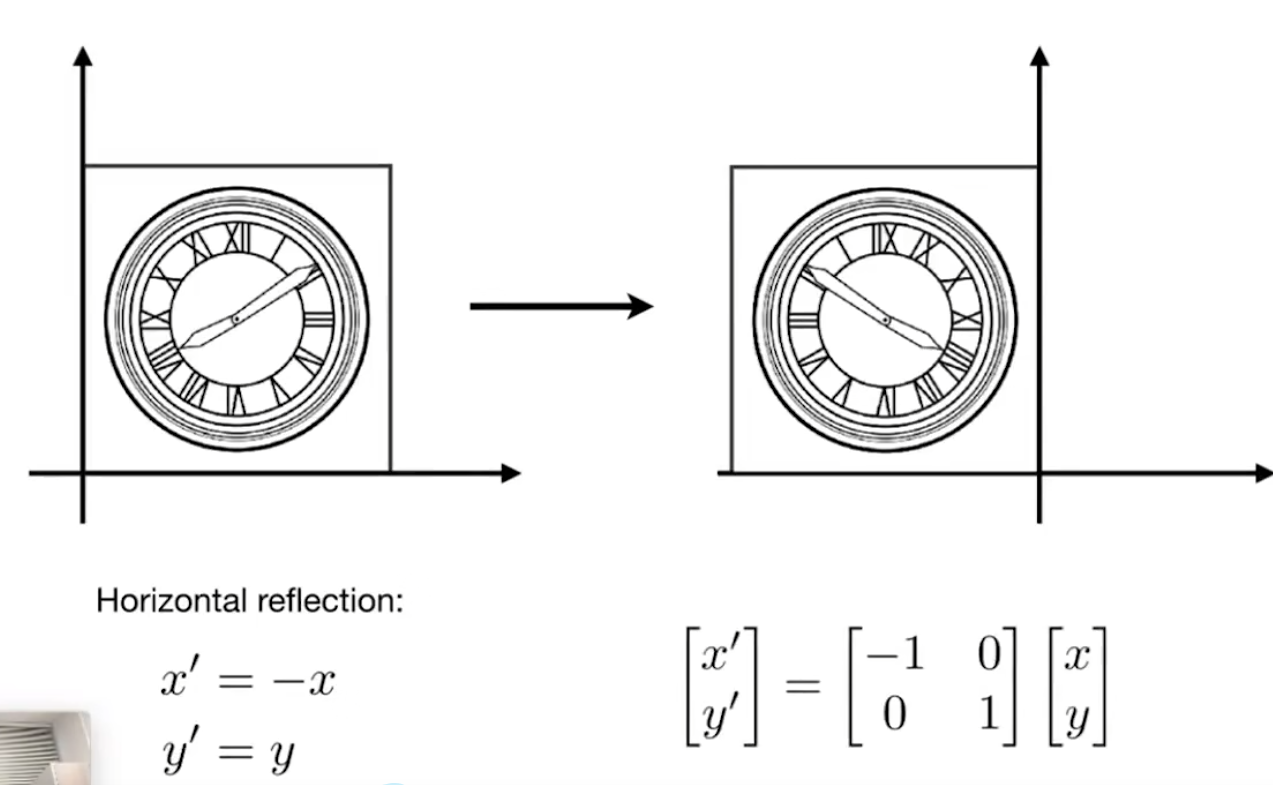
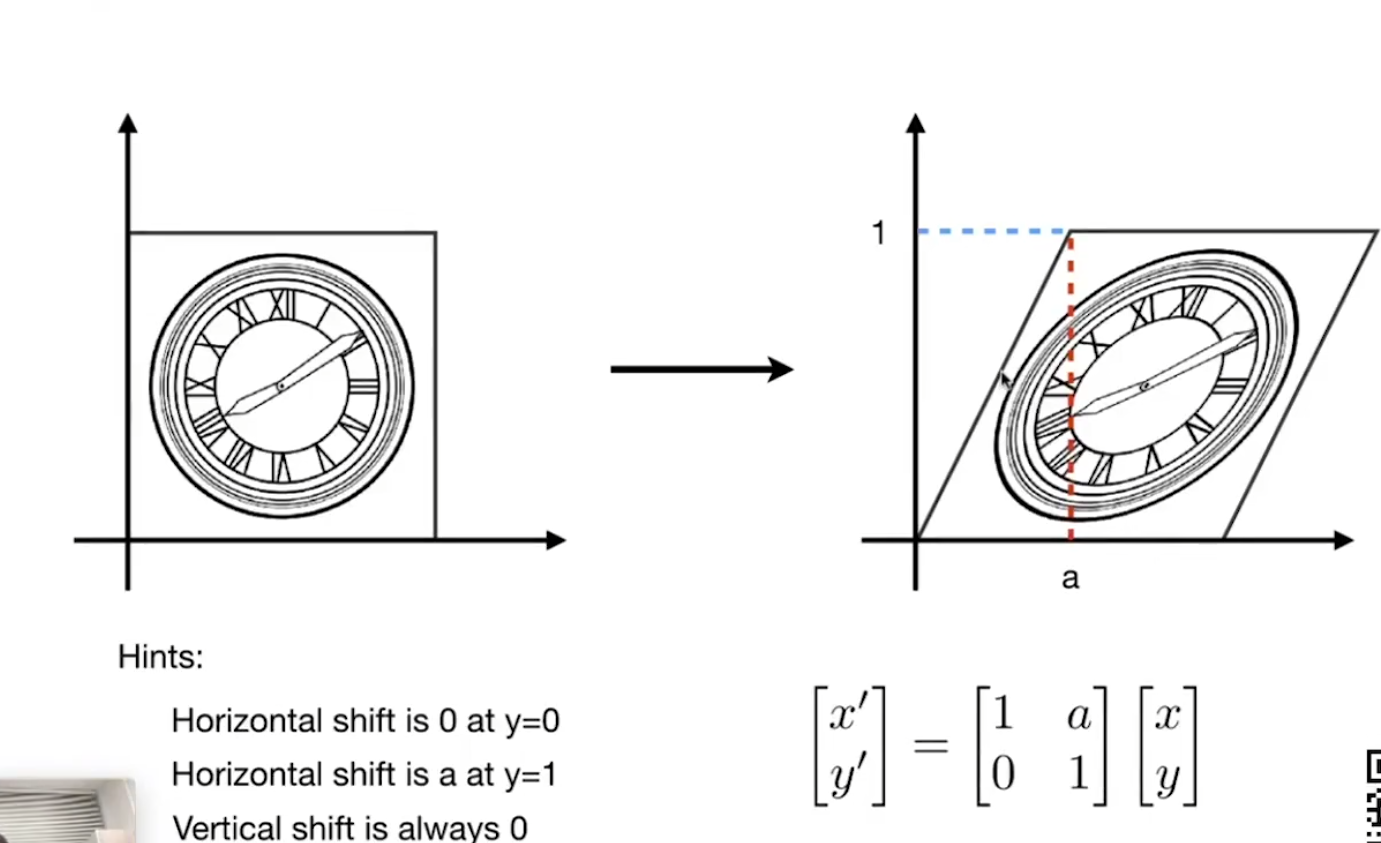
切变

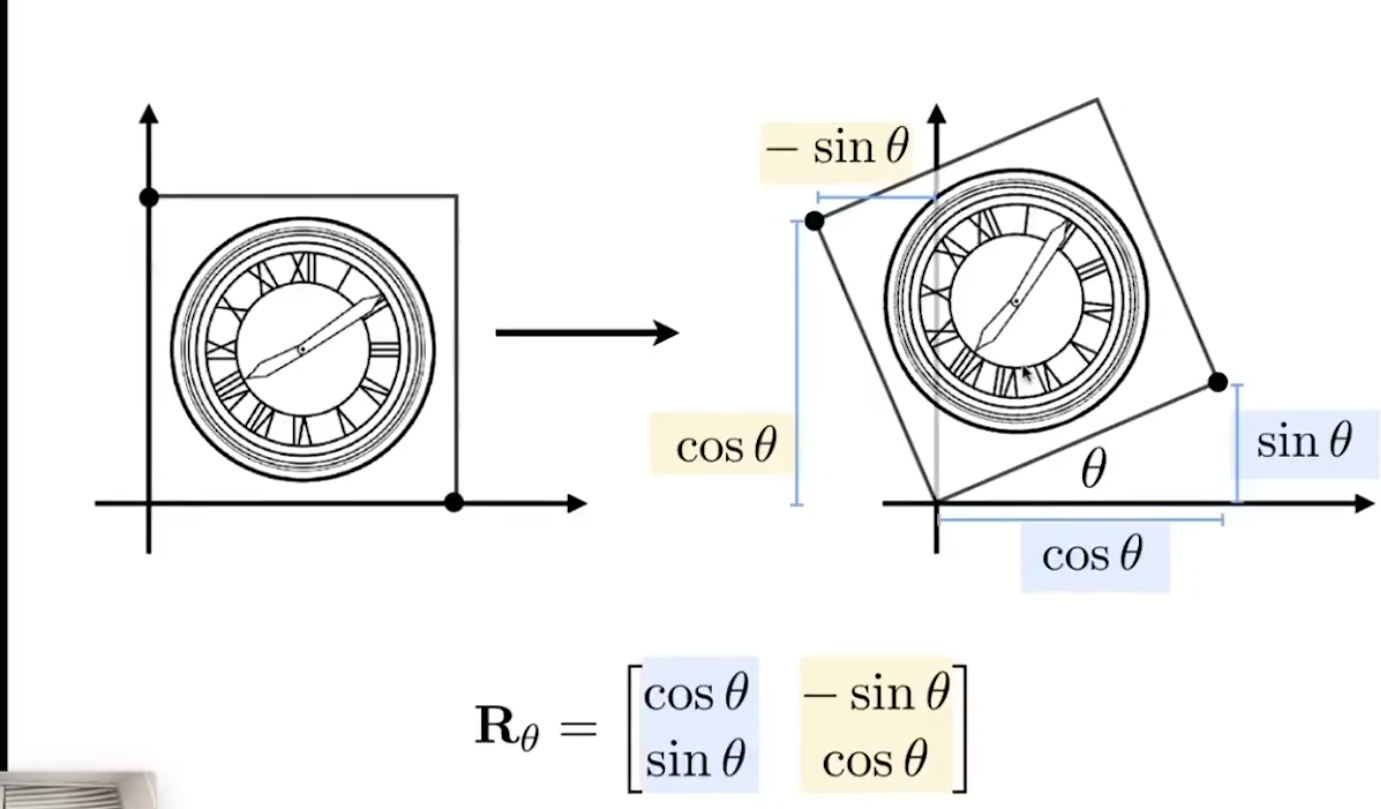
旋转

总结
缩放可以表示为矩阵的变换（线性变换）

在齐次坐标中 用 （x， y, 1)^T 表示点
用（x， y, 0)^T 表示向量

用齐次坐标表示平移操作

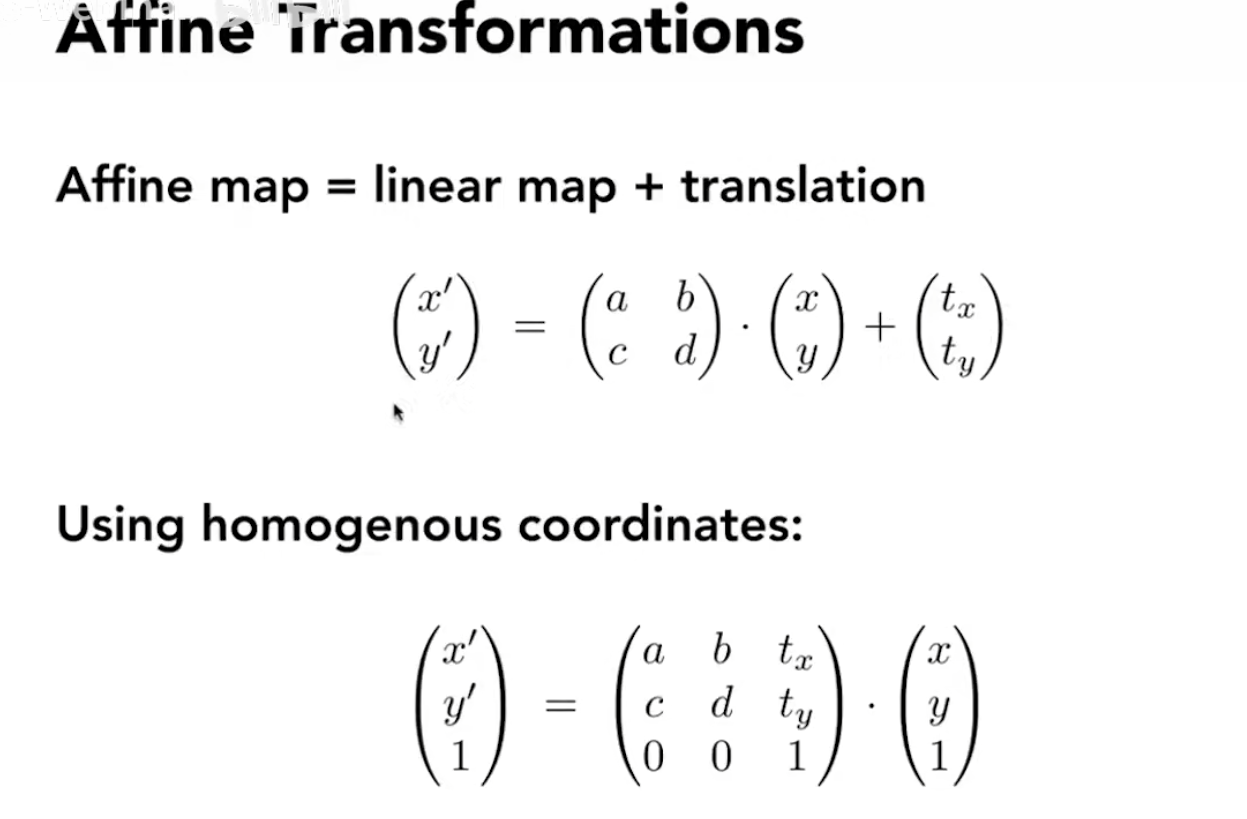
齐次坐标的线性操作