动态线性规划问题——以物资调度为例

物资调度问题在仓储工作中经常出现，人工调度的困难之一是因为有调度成本存在，对于调度物资的分配不仅仅是简单的供给与需求问题，还需要考虑成本最优。那么如何能实现成本最优且调配合理呢？本文通过floyd算法来分析这个问题。

一、问题描述

某地区各县市的分布情况如图所示，图中的边表示连接各县市的公路，边权值表示车辆通过该路段所需的时间。

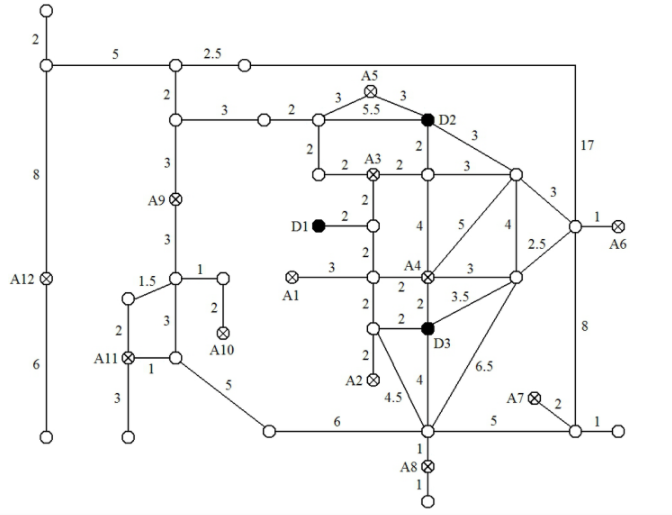
 现D1,D2,D3三地突发自然灾害，每天需要应急物资分别为100吨、80吨和60吨；而能提供应急物资的县市为A1,A2,......,A12,它们每天能提供（30, 15, 15, 20, 35, 40, 30, 20, 10, 25, 25, 30）吨的应急物资。如果A1,A2,......,A12各地所提供的应急物资，其成本分别为（2, 4, 5, 3, 1, 6, 2, 3, 6, 1, 5, 5）万元/吨，请设计一份经济快速的应急物资运送方案，使得每天都能保证D1,D2,D3三地对应急物资的需求。

二、基本假定与符号约定

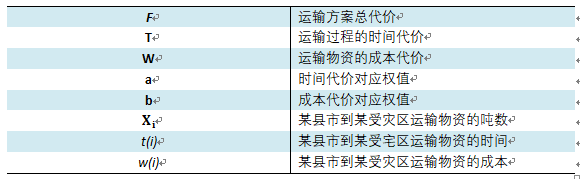
 运输物资的吨数

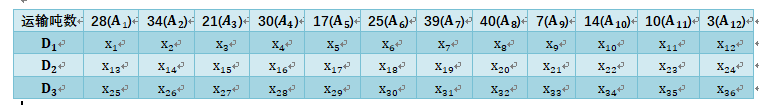
 三、问题的分析与模型的建立

3.1问题的分析

显然，给定的问题是一个优化问题，目标是经济快速的运输方案。分析题意可知，运送的总代价是时间代价T与成本代价W的总和。而时间代价是由每个物品运达到目的地的总和决定的，即时间代价总和T等于每一吨物资的时间总和∑xi*ti；而成本代价是由每一吨物品的总成本所决定的，即成本代价等于每一吨物资的成本总和Σxi*Wi。这两部分相互制约；时间代价越低，成本代价可能会越高，反之亦然。因此，原问题要求在时间代价和成本代价之间找到一种平衡，使得总代价最小。

我们通过函数F(x)=aT(x)+bW(x)（a+b=1,a0,b0）来对总代价也就是经济快速进行量化，结合实际情况对a,b参数的值进行调整，a值越大越侧重于节约时间，b值越大越侧重于节约成本。需要注意的是，因A12提供物资不能于当日到达，所以第一天需要单独考虑。

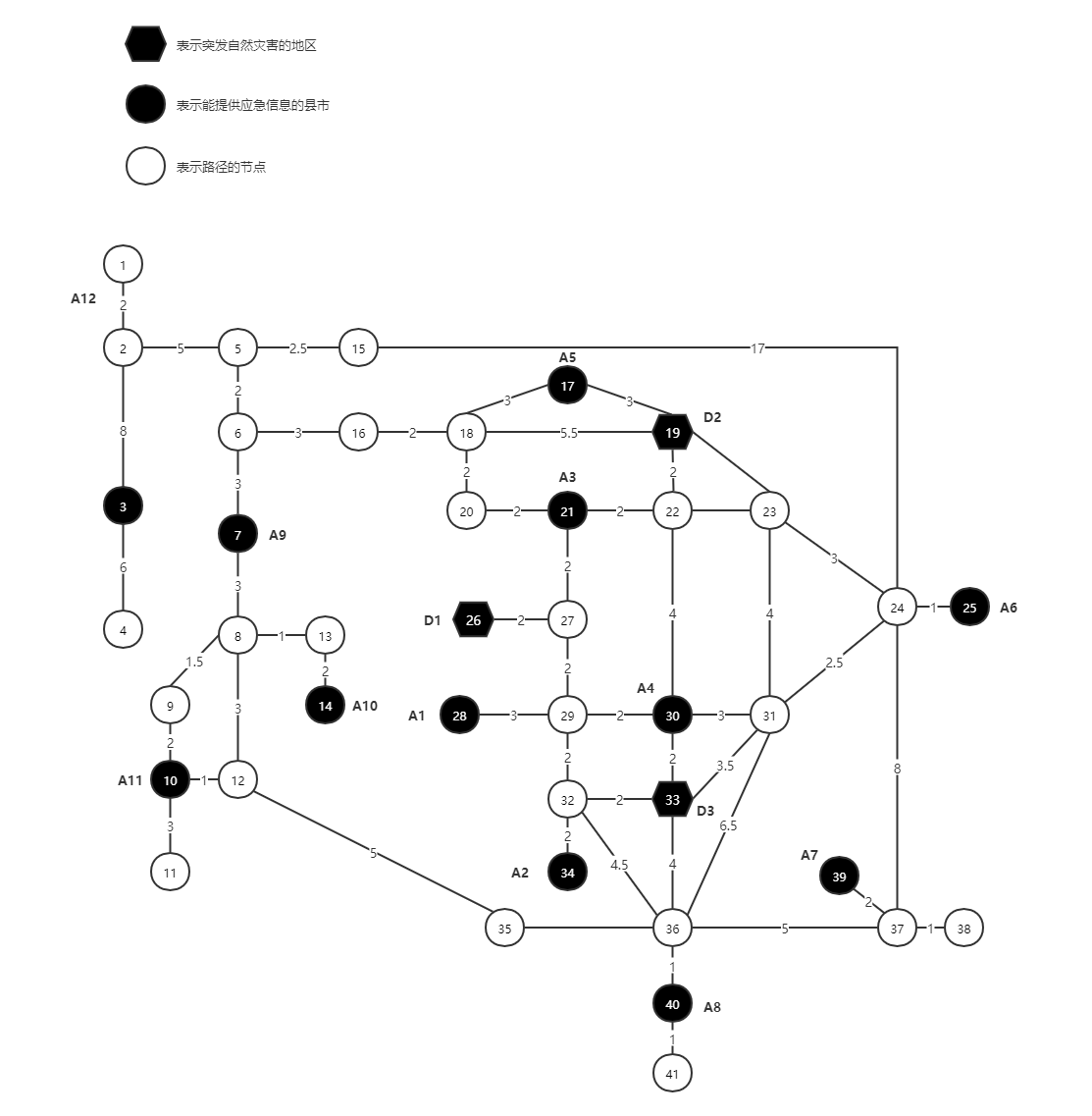
• 节点重编码

对题目所给路径模型各节点进行编码，编码后网络图如下：

• 求最短时间

通过floyd算法求解提供应急物资的县市对应结点到达突发自然灾害的地区对应结点的最算时间，所得结果如下表格所示

•  数学模型建立

 （备注：此处第二个等式的结果应该是80，第三个等式的结果应该是60）

•  编程求解结果

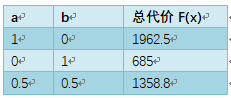
a=1,b=0时：

 F(x)=1962.5

a=0,b=1时：

  F(x)=685

a=0.5,b=0.5时：

   F(x)=1358.8

•  总结分析

上图表格分别展示了侧重于考虑时间、侧重于考虑成本，以及综合考虑时间与成本的分配方案。其中a=0.5,b=0.5仅为综合考虑时间与成本的一种情况，要获得具体的分配方案，则需要依据实际情况对a,b进行赋值。

通过表格1可以观察到A12提供应急物资到三个受灾地区的时间均超过24小时，其余地区均可在当天内送达。所以A12比较特殊，因为运送物资不能当天送达，其提供的物资将计入次日提供物资量。由于灾害发生后第一天内不能接收到A12的物资，所以第一天需要单独考虑。因此计算第一天分配方案时，则需要除去A12所对应的三个变量，得到部分总代价如下表

 四、附录

matlab求解线性规划

   a=1;
   b=0;
   f=[7*a+2*b;   8*a+4*b;   4*a+5*b;   6*a+3*b;   11*a+1*b;   12.5*a+6*b;   17.5*a+2*b;      11.5*a+3*b;   16*a+6*b;   22*a+1*b;   22.5*a+5*b;   
     11*a+2*b;  12*a+4*b;   4*a+5*b;   6*a+3*b;    3*a+1*b;      7*a+6*b;     16*a+2*b;     13*a+3*b; 13.5*a+6*b; 19.5*a+1*b;     20*a+5*b;
      7*a+2*b;   4*a+4*b;   8*a+5*b;   2*a+3*b;   11*a+1*b;      7*a+6*b;     11*a+2*b;      5*a+3*b;   20*a+6*b;   21*a+1*b;     16*a+5*b; ];
   A=[1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 
      0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 
      0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 
      0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 
      0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 
      0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 
      0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 
      0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 
      0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0  
      0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 
      0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 
      ];
   b=[30 15 15 20 35 40 30 20 10 25 25 ];
   Aeq=[1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
        0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0
        0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 ];
   beq=[100 80 60];
   lb=[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0];
   [x,fval]=linprog(f,A,b,Aeq,beq,lb,[])