斜率优化

[HNOI 2008] 玩具装箱

给你一个转移方程：
$$f_i = \min_{j \le i} \left \{ f_j+(\sum_{k=j+1}^{i}c_k + i-j-1+L)^2\right \}$$
其中 $i \le n \le 5 \times10^4$
朴素方程是 $O(n^3)$ 的，无法在规定时间内转移，我们需要想办法来优化它。
考虑前缀和，设 $pre_j = \sum_{i\le j} c_i$ 原式变成
$$f_i = \min_{j \le i} \left \{ f_j+(pre_i-pre_{j} + i-j-1+L)^2\right \}$$
转移复杂度是 $O(n^2)$ 的，还是不够。
我们把式子拆开，设 $s_i = pre_i+i$，$h_i=s_i+L+1$
原式变成
$$f_i = \min_{j \le i} \left \{ f_j+(s_i-h_j)^2 \right \}$$
把平方拆开
$$f_i-s_i^2 = \min_{j \le i} \left \{ f_j+h_j^2-2\times s_i \times h_j \right \}$$
考虑一次函数 $y=kx+b$，$b =y-kx$
令
$$y_j=f_j+h_j^2$$$$x_j=h_j$$
$$b_i=f_i-s_i^2$$$$k_i=2\times s_i$$
所以上式可以化成一次函数的形式 $b_i=y_j-k_ix_j$。
因为 $b$ 的实际意义是函数在坐标系中的截距，所以我们或许可以借助图像的性质来优化转移。 我们需要维护一个凹壳 $q$，其中 $\forall q_r < i$，$K(q_{r-1},q_r) \le K(q_r,q_{r+1})$。 观察下图

我们发现当斜率为 $k_i$ 时，最佳决策点为使得 $K(q_{e-1},q_e) \le k_i \le K(q_e,q_{e + 1})$ 的 $q_e$

再看为什么要维护凹壳，如图：

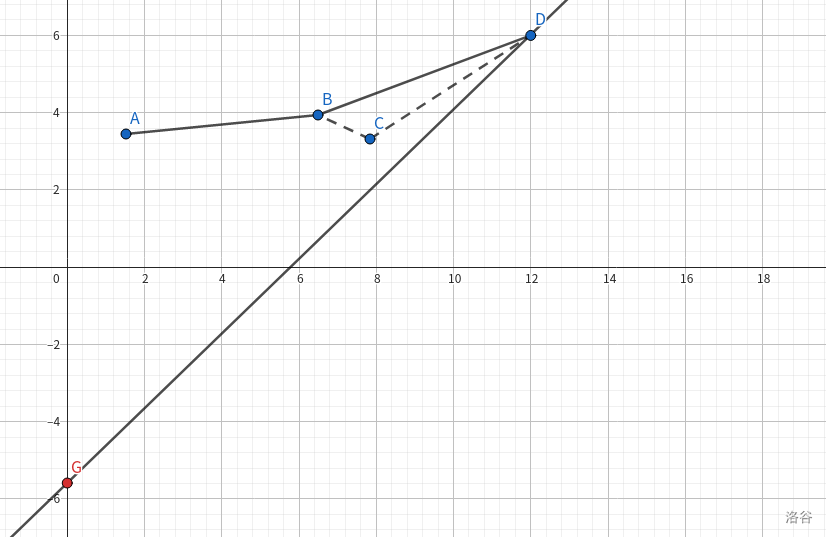
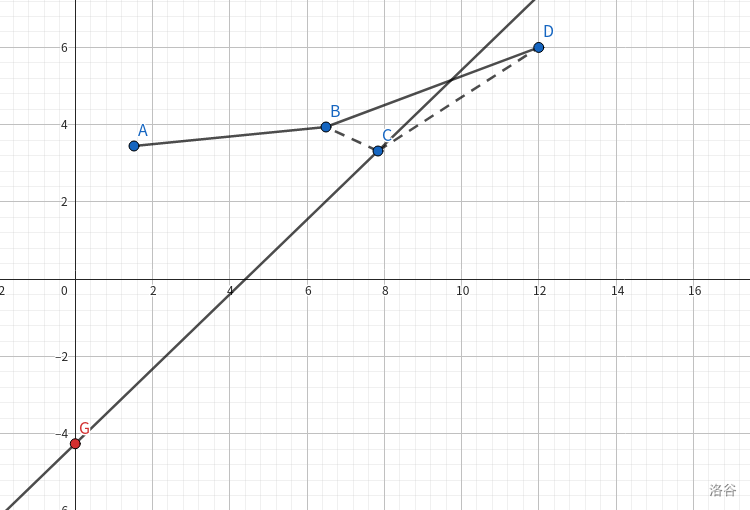
我们发现点 $C$ 是不会取的，因为不管选 $B$ 还是选 $D$ 都比 $C$ 更优。
再推一个转移时用的式子： 我们称一个点更优当且仅当
对于$\forall k <j<i$，有
$$f_j+(s_i-h_j)^2 < f_k + (s_i-h_k)^2$$
$$f_j-2s_ih_j+h_j^2 < f_k -2s_ih_k+h_k^2$$
$$2s_i\times(h_k-h_j) < (f_k+h_k^2) -(f_j+h_j^2)$$
$$2s_i < \frac{Y(k)-Y(j)}{X(k)-X(j)}$$
即有 $2s_i < K(k,j)$，我们称 $j$ 比 $k$ 更优。
至此，我们可以使用单调队列维护点集 $q$，做到 $O(n)$ 的转移。

Code

#include<bits/stdc++.h>
using namespace std;
const int N = 5e4 + 500;
typedef long long ll;
ll c[N], pre[N], s[N], dp[N], L, Ll;
int qu[N];
int n, to = 1, tl = 1;
ll X(int i) {return s[i] + Ll;}
ll Y(int i) {return dp[i] + X(i) * X(i);} 
ll KK(int i, int j) {return (Y(j) - Y(i)) / (X(j) - X(i));} 
int main() {
    scanf("%d %lld", &n, &L);
    Ll = L + 1;
    for(int i = 1;i <= n;i++) scanf("%lld", &c[i]);
    for(int i = 1;i <= n;i++) pre[i] = pre[i - 1] + c[i];
    for(int i = 1;i <= n;i++) s[i] = pre[i] + i;
    for(int i = 1;i <= n;i++) {
        while(to < tl && KK(qu[to], qu[to + 1]) < 2 * s[i]) to++;
        dp[i] = dp[qu[to]] + (s[i] - X(qu[to])) * (s[i] - X(qu[to]));
        while(to < tl && KK(qu[tl - 1], i) < KK(qu[tl - 1], qu[tl])) tl--;
        qu[++tl] = i; 
    }
    printf("%lld", dp[n]);
    return 0;   
}