第一章:二分法基础
1.1 基本概念与原理
二分法是一种在单调有序的集合或函数中查找解的高效算法。其核心思想是:
- 每次将搜索空间分为两部分
- 通过判断解的位置舍弃一半空间
- 逐步缩小范围直至找到目标
1.2 复杂度分析
- 整数域****:对于长度为N的区间,需要O(logN)次确定分界点
- 实数域****:通过判断区间长度(R-L)是否达到精度要求(如R-L≥eps)
- 指定次数t****时,最终区间长度为初始长度L除以2^t
- 总复杂度****:O(二分次数 × 单次判定复杂度)
1.3 实现模板
// 整数二分模板
int binary_search(int l, int r) {
while (l <= r) {
int mid = l + (r - l) / 2;
if (check(mid)) {
ans = mid;
l = mid + 1; // 或 r = mid - 1 根据情况调整
} else {
r = mid - 1; // 或 l = mid + 1
}
}
return ans;
}
// 实数二分模板
double binary_search(double l, double r) {
while (r - l > eps) {
double mid = (l + r) / 2;
if (check(mid)) l = mid;
else r = mid;
}
return l;
}
第二章:二分法常见模型
2.1 二分答案模型
适用场景****:"最小值最大"或"最大值最小"类问题
解题步骤****:
- 确定答案的可能范围
- 设计验证函数check(mid)
- 根据验证结果调整搜索区间
- 将最优化问题转化为判定性问题
示例****:将长度为n的序列分成最多m个连续段,求所有分法中每段和的最大值最小是多少。
2.2 二分查找模型
适用场景****:在有序集合中查找特定元素或满足条件的分界点
变种应用****:
- 查找第一个大于等于x的元素
- 查找最后一个小于等于x的元素
- 查找特定元素的出现次数
第三章:典型例题解析
例题1:愤怒的牛(Usaco2005 feb)
问题描述****:在n个牛舍中放置m头牛,最大化最近两头牛的距离。
解题思路****:
- 对牛舍位置排序
- 定义验证函数C(d):能否安排牛使最近距离≥d
- 贪心验证:按最小间距d放置牛
- 二分搜索最大的满足条件的d
参考代码****:
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 1e5 + 5;
int n, m, x[MAXN];
bool check(int d) {
int last = x[0], cnt = 1;
for (int i = 1; i < n; ++i) {
if (x[i] - last >= d) {
last = x[i];
if (++cnt >= m) return true;
}
}
return cnt >= m;
}
int main() {
cin >> n >> m;
for (int i = 0; i < n; ++i) cin >> x[i];
sort(x, x + n);
int l = 0, r = x[n-1] - x[0], ans = 0;
while (l <= r) {
int mid = l + (r - l) / 2;
if (check(mid)) ans = mid, l = mid + 1;
else r = mid - 1;
}
cout << ans << endl;
return 0;
}
例题2:最佳牛围栏(POJ2018)
问题描述****:求长度≥L的子段的最大平均数。
解题思路****:
- 二分平均数候选值
- 将数列每个元素减去该值
- 转化为求长度≥L的非负子段和
- 使用前缀和优化计算
参考代码****:
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 1e5 + 5;
const double eps = 1e-5;
int n, L;
double a[MAXN], sum[MAXN];
bool check(double avg) {
sum[0] = 0;
for (int i = 1; i <= n; ++i)
sum[i] = sum[i-1] + a[i] - avg;
double min_val = 0;
for (int i = L; i <= n; ++i) {
if (sum[i] - min_val >= 0) return true;
min_val = min(min_val, sum[i - L + 1]);
}
return false;
}
int main() {
cin >> n >> L;
double l = 0, r = 0;
for (int i = 1; i <= n; ++i) {
cin >> a[i];
r = max(r, a[i]);
}
while (r - l > eps) {
double mid = (l + r) / 2;
if (check(mid)) l = mid;
else r = mid;
}
cout << int(r * 1000) << endl;
return 0;
}
第四章:三分法
4.1 基本概念
用于求解单峰函数的极值问题。与二分法不同,三分法利用函数的单峰性而非单调性。
4.2 算法步骤
- 设当前区间为[l,r]
- 计算两个三等分点:
- m1 = l + (r-l)/3
- m2 = r - (r-l)/3
- 比较f(m1)和f(m2):
- 求最大值时:保留较大值所在区间
- 求最小值时:保留较小值所在区间
- 重复直至区间足够小
4.3 注意事项
- 仅适用于严格单峰函数
- 当f(m1)=f(m2)时,若函数非严格单调,可能无法确定如何缩小区间
4.4 参考代码
#include <iostream>
#include <cmath>
using namespace std;
// 示例单峰函数
double f(double x) {
return -x*x + 4*x + 5; // 在x=2处有最大值9
}
double ternary_search(double l, double r) {
while (r - l > 1e-6) {
double m1 = l + (r - l) / 3;
double m2 = r - (r - l) / 3;
if (f(m1) < f(m2)) l = m1; // 求最大值,保留较大区间
else r = m2;
}
return f(l);
}
int main() {
double l = 0, r = 5;
cout << "Maximum value: " << ternary_search(l, r) << endl;
return 0;
}
第五章:方法对比与应用选择
方法
适用条件
核心思想
关键操作
时间复杂度
二分法
单调函数/序列
每次舍弃一半空间
中点判断
O(logN)
三分法
单峰函数
利用极值点特性
三等分点比较
O(logN)
应用选择指南****:
- 单调性问题 → 二分法
- 单峰极值问题 → 三分法
- 最优化问题 → 考虑二分答案
- 有序数据查询 → 二分查找
第六章:常见问题与技巧
6.1 常见错误
- 区间更新错误(死循环或跳过解)
- 精度设置不当(实数二分)
- 验证函数设计错误
- 初始边界设置不合理
6.2 优化技巧
- 预处理数据(如排序)
- 使用前缀和优化验证过程
- 合理设置精度和终止条件
- 对大规模数据使用快速IO
第七章:扩展练习
- 在旋转有序数组中查找最小值
- 求解方程的实数根
- 寻找峰值元素
- 制作花束的最少天数
- 分配糖果问题
二分查找
二分查找
描述
请在一个有序递增数组中(不存在相同元素),采用二分查找,找出值x的位置,如果x在数组中不存在,请输出-1!
输入描述
第一行,一个整数n,代表数组元素个数(n <= 106)
第二行,n个数,代表数组的n个递增元素(1<=数组元素值<=108)
第三行,一个整数x,代表要查找的数(0<=x<=108)
输出描述
x在数组中的位置,或者-1。
用例输入 1
10
1 3 5 7 9 11 13 15 17 19
3
用例输出 1
2
#include <bits/stdc++.h>
using namespace std;
int main() {
int n,x,a[1000001],p=-1;
cin>>n;
for(int i=1; i<=n; i++) {
cin>>a[i];
}
cin>>x;
int left=1,right=n;
while(left<=right) {
int mid=(left+right)/2;
if(a[mid]==x) {
p=mid;
break;
}
if(a[mid]>x) {
right=mid-1;
}
else {
left=mid+1;
}
}
cout<<p;
return 0;
}
二分查找右侧边界
描述
请在一个有序不递减的数组中(数组中的值有相等的值),采用二分查找,找到最后1次出现值x的位置,如果不存在x请输出-1。
请注意:本题要求出q个x,每个x在数组中第一次出现的位置。
比如有6个数,分别是:1 2 2 2 3 3,那么如果要求3个数:3 2 5,在数组中最后一次出现的位置,答案是:6 4 -1。
输入描述
第一行,一个整数n,代表数组元素个数(n <= 105)
第二行,n个整数,用空格隔开,代表数组的n个元素(1<=数组元素的值<=108)
第三行,一个整数q,代表有要求出q个数最后一次出现的位置(q<=105)
第四行,q个整数,用空格隔开,代表要找的数(1<=要找的数<=10 8 )
输出描述
按题意输出位置或者-1。
用例输入 1
6
1 2 2 2 3 3
3
3 2 5
用例输出 1
6 4 -1
#include <bits/stdc++.h>
using namespace std;
int main() {
int n,x,p=-1,a[1000001]= {};
cin>>n;
for(int i=1; i<=n; i++) {
cin>>a[i];
}
cin>>x;
for(int i=0; i<x; i++) {
int t;
cin>>t;
p=-1;
int left=1,right=n;
while(left<=right) {
int mid=(left+right)/2;
if(a[mid]==t) {
p=mid;
left=mid+1;
} else if(a[mid]>t) {
right=mid-1;
} else {
left=mid+1;
}
}
cout<<p<<' ';
}
return 0;
}
二分查找满足条件的数
描述
请在一个有序不递减的数组中(数组中的值有相等的值),采用二分查找,找到第1个大于或等于元素x的位置,如果不存在,请输出-1。
请注意:本题要求出q个x,每个x在数组找到第1个大于或等于x的元素的位置。
比如有6个数,分别是:1 2 2 2 6 6,那么如果要求3个数:5 8 2,在数组中找到第1个大于或等于他们的位置,答案是:5 -1 2。
输入描述
第一行,一个整数n,代表数组元素个数(n <= 105)
第二行,n个整数,用空格隔开,代表数组的n个元素(1<=数组元素的值<=108)
第三行,一个整数q,代表有要查询q个数(q<=105)
第四行,q个整数,用空格隔开,代表查询的数(1<=要找的数<=10 8 )
输出描述
按题意输出位置或者-1。
用例输入 1
6
1 2 2 2 6 6
3
5 8 2
用例输出 1
5 -1 2
#include <bits/stdc++.h>
using namespace std;
int main() {
int n,x,y;
cin>>n;
int a[n+1];
for(int i=1; i<=n; i++) {
cin>>a[i];
}
cin>>y;
for(int i=0; i<y; i++) {
cin>>x;
int l=1,r=n,m,p=-1;
while(l<=r) {
m=(l+r)/2;
if(a[m]>=x) {
p=m;
r=m-1;
} else {
l=m+1;
}
}
cout<<p<<' ';
}
return 0;
}
二分查找左侧边界
描述
请在一个有序不递减的数组中(数组中有相等的值),采用二分查找,找到值x 第1次出现 的位置,如果不存在x请输出-1。
请注意:本题要求出q个x,每个x在数组中第一次出现的位置。
比如有6个数,分别是:1 2 2 2 3 3,那么如果要求3个数:3 2 5,在数组中第一次出现的位置,答案是:5 2 -1。
输入描述
第一行,一个整数n,代表数组元素个数(n <= 105)
第二行,n个整数,用空格隔开,代表数组的n个元素(1<=数组元素的值<=108)
第三行,一个整数q,代表有要求出q个数首次出现的位置(q<=105)
第四行,q个整数,用空格隔开,代表要找的数(1<=要找的数<=108)
输出描述
输出1行,含q个整数,按题意输出要找的每个数在数组中首次出现的位置,如果不存在这样的数,请输出-1。
用例输入 1
6
1 2 2 2 3 3
3
3 2 5
用例输出 1
5 2 -1
#include<bits/stdc++.h>
using namespace std;
int n,a[100005],q;
int main() {
cin>>n;
for(int i=1; i<=n; i++) {
scanf("%d",&a[i]);
}
cin>>q;
while(q--) {
int x;
cin>>x;
int L=1,R=n,ans=-1;
while(L<=R) {
int mid=(L+R)/2;
if(a[mid]==x) {
ans=mid;
R=mid-1;
} else if(a[mid]>x) {
R=mid-1;
} else {
L=mid+1;
}
}
cout<<ans<<' ';
}
return 0;
}
【例83.2】二分查找
描述
对有序数组进行二分查找,是一种性能卓越的算法:目标是在有序数组a[]中查找是否有a[k]=key,若有返回_k_,否则返回−1。
- 若有多个
a[k]=key,请输出最小的_k_。 - 下标_k_从1开始计数。
输入描述
第一行包含1个整数_N_,代表数组长度。
第二行包含_N_个(N_≤30000)int范围内的整数,保证升序,空格隔开。
第三行包含1个整数_T,代表有_T_组询问。
第四行包含_T_个(_T_≤30000)int范围内的整数,表示每组询问需要查找的_k__e__y_值,空格隔开。
输出描述
一行,对于每组询问输出结果(k or -1),空格隔开。
用例输入 1
3
-2 -2 1
3
-2 -2 -1
用例输出 1
1 1 -1
#include <iostream>
using namespace std;
int main() {
int N;
cin >> N;
int a[30000]; // 根据题目要求,N≤30000
for (int i = 0; i < N; i++) {
cin >> a[i];
}
int T;
cin >> T;
int keys[30000]; // 根据题目要求,T≤30000
for (int i = 0; i < T; i++) {
cin >> keys[i];
}
// 处理每个查询
for (int i = 0; i < T; i++) {
int key = keys[i];
int left = 0;
int right = N - 1;
int result = -1;
// 二分查找
while (left <= right) {
int mid = left + (right - left) / 2;
if (a[mid] == key) {
result = mid; // 记录找到的位置
right = mid - 1; // 继续在左半部分查找更小的下标
} else if (a[mid] < key) {
left = mid + 1;
} else {
right = mid - 1;
}
}
// 输出结果(下标从1开始)
if (i != 0) cout << " ";
cout << (result == -1 ? -1 : result + 1);
}
return 0;
}
练83.5 二分查找2
描述
对有序数组进行二分查找,是一种性能卓越的算法:目标是在有序数组a[]中查找是否有a[k]=key,若有返回_k_,否则返回−1。
- 若有多个
a[k]=key,请输出最大的_k_。 - 下标_k_从1开始计数。
输入描述
第一行包含1个整数_N_,代表数组长度。
第二行包含_N_个(N_≤30000)int范围内的整数,保证升序,空格隔开。
第三行包含1个整数_T,代表有_T_组询问。
第四行包含_T_个(_T_≤30000)int范围内的整数,表示每组询问需要查找的_k__e__y_值,空格隔开。
输出描述
一行,对于每组询问输出结果(k 或 −1),空格隔开。
用例输入 1
4
-2 -2 -2 1
3
-2 -2 -1
用例输出 1
3 3 -1
#include <iostream>
using namespace std;
int main() {
int N;
cin >> N;
int a[30000];
for (int i = 0; i < N; ++i) {
cin >> a[i];
}
int T;
cin >> T;
int keys[30000];
for (int i = 0; i < T; ++i) {
cin >> keys[i];
}
for (int i = 0; i < T; ++i) {
int key = keys[i];
int left = 0, right = N - 1;
int result = -1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (a[mid] == key) {
result = mid; // 找到可能的k,继续向右查找更大的k
left = mid + 1;
} else if (a[mid] < key) {
left = mid + 1;
} else {
right = mid - 1;
}
}
if (result != -1) {
cout << result + 1 << " "; // 下标从1开始计数
} else {
cout << -1 << " ";
}
}
return 0;
}
练83.5 二分查找2
描述
对有序数组进行二分查找,是一种性能卓越的算法:目标是在有序数组a[]中查找是否有a[k]=key,若有返回_k_,否则返回−1。
- 若有多个
a[k]=key,请输出最大的_k_。 - 下标_k_从1开始计数。
输入描述
第一行包含1个整数_N_,代表数组长度。
第二行包含_N_个(N_≤30000)int范围内的整数,保证升序,空格隔开。
第三行包含1个整数_T,代表有_T_组询问。
第四行包含_T_个(_T_≤30000)int范围内的整数,表示每组询问需要查找的_k__e__y_值,空格隔开。
输出描述
一行,对于每组询问输出结果(k 或 −1),空格隔开。
用例输入 1
4
-2 -2 -2 1
3
-2 -2 -1
用例输出 1
3 3 -1
#include <iostream>
using namespace std;
int main() {
int N;
cin >> N;
int a[30000];
for (int i = 0; i < N; ++i) {
cin >> a[i];
}
int T;
cin >> T;
int keys[30000];
for (int i = 0; i < T; ++i) {
cin >> keys[i];
}
for (int i = 0; i < T; ++i) {
int key = keys[i];
int left = 0, right = N - 1;
int result = -1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (a[mid] == key) {
result = mid; // 找到可能的k,继续向右查找更大的k
left = mid + 1;
} else if (a[mid] < key) {
left = mid + 1;
} else {
right = mid - 1;
}
}
if (result != -1) {
cout << result + 1 << " "; // 下标从1开始计数
} else {
cout << -1 << " ";
}
}
return 0;
}
【入门】起止位置
描述
有n位同学按照年龄从小到大排好队。
王老师想要查询,年龄为x的同学,在队伍中首次出现的位置和最后一次出现的位置;如果队伍中不存在年龄为x的同学,请输出-1。
由于人数太多,一个一个数,太慢啦,请你编程求解。
请注意:本题中王老师查询年龄x出现的起止位置,并不是查询了1次,而是查询了q次。
比如:
假设有6位同学的年龄为:1 2 2 2 3 3,王老师查询了4个年龄,分别是2 1 3 8,那么:
年龄为2的同学首次和最后一次出现的位置分别是:2 4;
年龄为1的同学首次和最后一次出现的位置分别是:1 1;
年龄为3的同学首次和最后一次出现的位置分别是:5 6;
年龄为8的同学首次和最后一次出现的位置分别是:-1 -1;
输入描述
第一行包含整数n和q,表示队伍中的总人数和询问个数。
第二行包含n个整数(均在1~10000范围内),表示队伍中每个人的年龄。
接下来q行,每行包含一个整数x,表示一次询问的值。
输出描述
共q行,每行包含两个整数,表示所求年龄在队伍中的起始位置和终止位置。
如果数组中不存在该元素,则返回"-1 -1"。
数据范围
1≤n≤100000
1≤q≤10000
1≤x≤10000
用例输入 1
6 3
1 2 2 2 3 3
2
1
8
用例输出 1
2 4
1 1
-1 -1
#include<bits/stdc++.h>
using namespace std;
int n,a[100005],q;
int main() {
cin>>n;
cin>>q;
for(int i=1; i<=n; i++) {
scanf("%d",&a[i]);
}
while(q--) {
int x;
cin>>x;
int L=1,R=n,ans=-1;
while(L<=R) {
int mid=(L+R)/2;
if(a[mid]==x) {
ans=mid;
R=mid-1;
} else if(a[mid]>x) {
R=mid-1;
} else {
L=mid+1;
}
}
cout<<ans<<' ';
L=1,R=n,ans=-1;
while(L<=R) {
int mid=(L+R)/2;
if(a[mid]==x) {
ans=mid;
L=mid+1;
} else if(a[mid]>x) {
R=mid-1;
} else {
L=mid+1;
}
}
cout<<ans<<' ';
cout<<endl;
}
return 0;
}
【基础】同时出现的数
描述
Medusa同学拿到了2组数字,老师请你编程帮他找出,第2组数中的哪些数,在第1组数中出现了,从小到大输出所有满足条件的数。
比如:
第1组数有:8 7 9 8 2 6 3
第2组数有:9 6 8 3 3 2 10
那么应该输出:2 3 3 6 8 9
输入描述
第一行两个整数n和m,分别代表2组数的数量
第二行n个正整数
第三行m个正整数
输出描述
按照要求输出满足条件的数,数与数之间用空格隔开
用例输入 1
7 7
8 7 9 8 2 6 3
9 6 8 3 3 2 10
用例输出 1
2 3 3 6 8 9
提示
对于60%的数据1≤n,m≤1000,每个数<=2x109
对于100%的数据1≤n,m≤100000,每个数<=2x109
#include<bits/stdc++.h>
using namespace std;
int n,a[1000000],b[1000000],x,q;
int main() {
cin>>n>>q;
for(int l=1; l<=n; l++) cin>>a[l];
for(int i=1; i<=q; i++) cin>>b[i];
sort(a+1,a+1+n);
sort(b+1,b+1+q);
for(int i=1; i<=q; i++) {
int l=1,r=n;
int ans=-1;
while(l<=r) {
int mid=(l+r)/2;
if(a[mid]==b[i]) {
ans=mid;
break;
} else if(a[mid]>b[i]) {
r=mid-1;
} else if(a[mid]<b[i]) {
l=mid+1;
}
}
if(ans!=-1) cout<<b[i]<<" ";
}
return 0;
}
【基础】最满意的方案
描述
高考结束了,同学们要开始了紧张的填写志愿的过程,大家希望找一个自己最满意的大学填报方案,请你编程帮忙实现。
现有m(m≤100000)所学校,每所学校预计分数线是ai(ai≤106)。有 n(n≤100000)位学生,估分分别为 bi(bi≤106)。
根据n位学生的估分情况,分别给每位学生推荐一所学校,要求学校的预计分数线和学生的估分相差最小(可高可低,毕竟是估分嘛),这个最小值为不满意度。求所有学生不满意度和的最小值。
输入描述
第一行读入两个整数m,n。m表示学校数,n表示学生数。第二行共有m个数,表示m个学校的预计录取分数。第三行有n个数,表示n个学生的估分成绩。
输出描述
一行,为最小的不满度之和。(数据保证结果<=1010)
用例输入 1
4 3
513 598 567 689
500 600 550
用例输出 1
32
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+1;
int main() {
int m,n,a[N]= {};
cin>>m>>n;
for(int i=0; i<m; i++) {
cin>>a[i];
}
sort(a,a+m);
int res=0;
while(n--) {
int t;
cin>>t;
int left=0,right=m-1,mid=0,p=0;
while(left<=right) {
mid=(left+right)/2;
if(a[mid]<=t) {
p=mid;
left=mid+1;
} else {
right=mid-1;
}
}
if(t<=a[0]) {
res+=a[0]-t;
} else if(t>=a[m-1]) {
res+=t-a[m-1];
} else {
int t1=min(t-a[p],a[p+1]-t);
res+=t1;
}
}
cout<<res;
return 0;
}
二分答案
伐木工
描述
伐木工人米尔科需要砍倒M米长的木材。这是一个对米尔科来说很容易的工作,因为他有一个漂亮的新伐木机,可以像野火一样砍倒森林。不过,米尔科只被允许砍倒单行树木。
米尔科的伐木机工作过程如下:米尔科设置一个高度参数H(米),伐木机升起一个巨大的锯片到高度H,并锯掉所有的树比H高的部分(当然,树木不高于H米的部分保持不变)。米尔科就行到树木被锯下的部分。
例如,如果一行树的高度分别为20,15,10和17,米尔科把锯片升到15米的高度,切割后树木剩下的高度将是15,15,10和15,而米尔科将从第1棵树得到5米,从第4棵树得到2米,共得到7米木材。
米尔科非常关注生态保护,所以他不会砍掉过多的木材。这正是他为什么尽可能高地设定伐木机锯片的原因。帮助米尔科找到伐木机锯片的最大的整数高度H,使得他能得到木材至少为M米。换句话说,如果再升高1米,则他将得不到M米木材。
输入描述
第1行:2个整数N和M,N表示树木的数量(1<=N<=106),M表示需要的木材总长度(1<=M<=2 * 109)
第2行:N个整数表示每棵树的高度,值均不超过109。所有木材长度之和大于M,因此必有解。
输出描述
1个整数,表示砍树的最高高度。
用例输入 1
5 20
4 42 40 26 46
用例输出 1
36
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,m;
int a[1000005];
cin>>n>>m;
for(int i=0;i<n;i++){
cin>>a[i];
}
int l=0;
int r=1000000000;
int ans=0;
while(l<=r){
int mid=(l+r)/2;
long sum=0;
for(int i=0;i<n;i++){
if(mid<a[i]){
sum+=a[i]-mid;
}
}
if(sum<m){
r=mid-1;
}else{
l=mid+1;
ans=mid;
}
}
cout<<r;
return 0;
}
【提高】跳石头
描述
一年一度的“跳石头”比赛又要开始了!
这项比赛将在一条笔直的河道中进行,河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间,有 N 块岩石(不含起点和终点的岩石)。在比赛过程中,选手们将从起点出发,每一步跳向相邻的岩石,直至到达终点。
为了提高比赛难度,组委会计划移走一些岩石,使得选手们在比赛过程中的最短跳跃距离尽可能长。由于预算限制,组委会至多从起点和终点之间移走 M 块岩石(不能移走起点和终点的岩石)。
输入描述
第一行包含三个整数 L,N,M ,分别表示起点到终点的距离,起点和终点之间的岩石数,以及组委会至多移走的岩石数。保证L≥1 且 N≥M≥0 。
接下来 N 行,每行一个整数,第 i 行的整数 Di( 0 < Di < L), 表示第 i 块岩石与起点的距离。这些岩石按与起点距离从小到大的顺序给出,且不会有两个岩石出现在同一个位置。
输出描述
一个整数,即最短跳跃距离的最大值。
用例输入 1
25 5 2
2
11
14
17
21
用例输出 1
4
提示
输入输出样例1说明:将与起点距离为 2 和 14 的两个岩石移走后,最短的跳跃距离为 4 (从与起点距离 17 的岩石跳到距离 21 的岩石,或者从距离 21 的岩石跳到终点)。
另:
对于20% 的数据, 0≤M≤N≤10 。
对于 50% 的数据,0≤M≤N≤100 。
对于 100% 的数据, 0≤M≤N≤50,000,1≤L≤1,000,000,000 。
【来源】NOIP2015提高组复赛day2。
#include <bits/stdc++.h>
using namespace std;
int l,n,m,a[50001];
bool f(int x){
int d=0,cnt=0;
for(int i=0;i<n;i++){
if(a[i]-d<x){
cnt++;
}else{
d=a[i];
}
}
return cnt<=m;
}
int main() {
cin>>l>>n>>m;
for(int i=0;i<n;i++){ cin>>a[i]; }
int left=0, right=l;
while(left<=right){
int mid=(left+right)/2;
if(f(mid)){
left=mid+1;
}else{
right=mid-1;
}
}
cout<<right;
return 0;
}
【提高】买木头
描述
有n个木材供应商(1≤n≤10000),每个供货商有长度相同一定数量的木头。长木头可以锯短,但短木头不能接长。有一个客人要求m根长度相同的木头。
要求计算出,此时供货商提供的木头满足客人要求的最长的长度是多少。
例如n=2,m=30,两个供货商的木头为:
12,10 第1个供货商的木头长度为12,共有10根
5,10 第2个供货商的木头长度为5,共有10根。
计算的结果为5,即长度为12的木头一根可锯出两根长度为5的木头,多余的无用,长度为5的木头不动,此时可得到30根长度为5的木头。
输入描述
整数n,m,l1,s1(1≤m≤1000000,1≤l_1≤10000,1≤s_1≤100)
其中l1是第一个供货商木头的长,s1是第一个供货商木头数量。其他供货商木头的长度和数量li和si(i≥2),由下面的公式给出:
li=((l(i-1)×37011+10193) mod 10000)+1
si=((s(i-1)×73011+24793) mod 100)+1
输出描述
一个整数,即满足要求的m根长度相同的木头的最大长度。
用例输入 1
10 10000 8 20
用例输出 1
201
来源
省赛 数组问题 二维数组 结构体
#include<bits/stdc++.h>
using namespace std;
const int N = 1000010;
long long n, m, l[N], s[N];
bool check(long long x) {
long long cnt = 0;
for (int i = 0; i < n; i++)cnt += (l[i] / x) * s[i];
return cnt >= m;
}
int main() {
cin.tie(0);
cin >> n >> m >> l[0] >> s[0];
for (int i = 1; i < n; i++) {
l[i] = ((l[i - 1] * 37011 + 10193) % (10000)) + 1;
s[i] = ((s[i - 1] * 73011 + 24793) % (100)) + 1;
}
long long l = 1, r = 1e18, ans = 0;
while (l <= r) {
long long mid = (l + r) >> 1;
if (check(mid)) {
ans = mid;
l = mid + 1;
} else r = mid - 1;
}
cout << ans;
return 0;
}
【基础】愤怒的奶牛 USACO
描述
Farmer John建造了一个有N(2<=N<=100,000)个隔间的牛棚,这些隔间分布在一条直线上,坐标是x1,…,xN (0<=xi<=1,000,000,000)。
他的C(2<=C<=N)头牛不满于隔间的位置分布,它们为牛棚里其他的牛的存在而愤怒。为了防止牛之间的互相打斗,Farmer John想把这些牛安置在指定的隔间,所有牛中相邻两头的最近距离越大越好。那么,这个最大的最近距离是多少呢?
输入描述
第1行:两个用空格隔开的数字N和C。
第2~N+1行:每行一个整数,表示每个隔间的坐标。
输出描述
输出只有一行,即相邻两头牛最大的最近距离。
用例输入 1
5 3
1
2
8
4
9
用例输出 1
3
来源
USACO 二分
#include<bits/stdc++.h>
using namespace std;
int a[100005];
int n,m;
int check(int d)//判断一下此间隔是否适用
{
int sign = d+a[1];
int sum = 1;
for(int i=2;i<=n;i++){
if(a[i]<sign)
continue;
sign = a[i]+d;
sum++;
}
return sum>=m;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
sort(a+1,a+n+1);//必须排序,二分查找要求是单调序列
int l=0,r=a[n]-a[1],mid;
while(l<=r){//二分查找最小的间隔
mid = (r+l)>>1;
if(check(mid))
l = mid+1;
else
r = mid-1;
}
printf("%d\n",r);
return 0;
}
【基础】最小的空旷指数
描****述
A市和B市之间有一条长长的高速公路,这条公路的某些地方设有路标,但是大家都感觉路标设得太少了,相邻两个路标之间往往隔着相当长的一段距离。为了便于研究这个问题,我们把公路上相邻路标的最大距离定义为该公路的“空旷指数”。
现在政府决定在公路上增设一些路标,使得公路的“空旷指数”最小。他们请求你设计一个程序计算能达到的最小值是多少。请注意,公路的起点和终点保证已设有路标,公路的长度为整数,并且原有路标和新设路标都必须距起点整数个单位距离。
输入描述
第1行包括三个数L、N、K,分别表示公路的长度,原有路标的数量,以及最多可增设的路标数量。
第2行包括N个整数(这N个数并未排序),分别表示原有的N个路标的位置。路标的位置用距起点的距离表示,且一定位于区间[0,L]内。
输出描述
输出1行,包含一个整数,表示增设路标后能达到的最小“空旷指数”值。
用例输入 1
101 2 1
0 101
用例输出 1
51
提示
【样例说明】
公路原来只在起点和终点处有两个路标,现在允许新增一个路标,应该把新路标设在距起点50或51个单位距离处,这样能达到最小的空旷指数51。
【数据范围】
50%的数据中,2 ≤ N ≤100,0 ≤K ≤100
100%的数据中,2 ≤N ≤100000, 0 ≤K ≤100000
100%的数据中,0 < L ≤10000000
#include <bits/stdc++.h>
using namespace std;
const int M = 100000;
int main() {
int L, N, K;
cin >> L >> N >> K;
int m[M];
for (int i = 0; i < N; ++i) {
cin >> m[i];
}
sort(m, m + N);
int l = 1, r = L, ans = L;
while (l <= r) {
int mid = l + (r - l) / 2;
int cnt = 0;
for (int i = 1; i < N; ++i) {
int d = m[i] - m[i - 1];
cnt += (d - 1) / mid;
}
if (cnt <= K) {
ans = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
cout << ans << endl;
return 0;
}
【提高】防御迷阵
描述
一队士兵来到了敌军城外,准备进攻敌城。敌人在城外布置一个防御迷阵,要进入城池首先必须通过城池外的防御迷阵。
迷阵由n*m个相同的小房间组成,每个房间与相邻四个房间之间有门可通行。而第1行的m个房间有m扇向外打开的门,是迷阵的入口。除了第1行和第n的房间外,每个房间都安装了激光杀伤装置,将会对进入房间的人造成一定的伤害。第i行第j列造成的伤害值为a[i,j]。 (第1行和第n行的a值全部为0)。
现在士兵打算以最小伤害代价通过迷阵,显然,他们可以选择任意多的人从任意的门进入,但必须到达第n行的房间。一个士兵受到的伤害值为他在经过的路径上所有房间的伤害值中的最大值。现在,士兵们掌握了迷阵的情况,他们需要提前知道怎么安排士兵的行进路线可以使得伤害值最小。
输入描述
第一行有两个整数n,m表示迷阵的大小。
接下来n行,每行m个数,第i行第j列的数表示a[i,j]。
输出描述
输出一个数,表示最小伤害代价。
用例输入 1
4 2
0 0
3 5
2 4
0 0
用例输出 1
3
提示
【数据范围】
n,m≤1000,a[i,j]≤1000
#include <bits/stdc++.h>
using namespace std;
bool f[1100][1100];//标记
int q[1000100][3];//队列
int a[1100][1100];
int fx[5] = {0, 1, 0, -1, 0};
int fy[5] = {0, 0, 1, 0, -1};
int n,m;
//判断从xy点开始,在伤害值最大为mid的情况下能否走到最后一行
bool bfs(int x,int y,int mid){
int head=1,tail=1;
memset(f,0,sizeof(f));//标记所有点没有走过
int tx,ty;
//出发点
q[1][1] = x;
q[1][2] = y;
while(head <= tail){
for(int i = 1;i <= 4;i++){
tx = q[head][1] + fx[i];
ty = q[head][2] + fy[i];
// cout<<tx<<" "<<ty<<" "<<a[tx][ty]<<endl;
//不满足要求,尝试其他点
if(tx<1||tx>n||ty<1||ty>m||f[tx][ty]||a[tx][ty]>mid)
continue;
if(tx==n) return true;//到终点
else{
tail++;
q[tail][1] = tx;
q[tail][2] = ty;
f[tx][ty] = 1;//标记该点走过
}
}
head++;
}
return false;
}
int main(){
int l = INT_MAX,r = INT_MIN,mid,ans;
cin>>n>>m;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
cin>>a[i][j];
r = max(r,a[i][j]);
l = min(l,a[i][j]);
}
}
// cout<<bfs(1,1,2)<<endl;
// return 0;
//在伤害值的最大和最小之间找
while(l <= r){
mid = l + r >> 1;
//mid可行,说明mid还能再小
if(bfs(1,1,mid)){
r = mid - 1;
}else l = mid + 1;//mid不行,说明太小,放大mid
}
//找左边界
cout<<l;
return 0;
}
Best Cow Fences
出题人:
描述
给定一个长度为 n 的非负整数序列 A ,求一个平均数最大的,长度不小于 L 的子段。
输入描述
第一行用空格分隔的两个整数 n 和 L;
第二行为 n 个用空格隔开的非负整数,表示 A__i。
输出描述
输出一个整数,表示这个平均数的 1000 倍。不用四舍五入,直接输出。
用例输入 1
10 6
6 4 2 10 3 8 5 9 4 1
用例输出 1
6500
提示
数据范围与提示
1≤_n_≤1e5,0≤_Ai_≤2000。
#include <bits/stdc++.h>
using namespace std;
const int N = 100005;
int n, L; // n为序列长度,L为最小子段长度
int a[N]; // 存储输入序列
double S[N]; // 前缀和数组
double min_S[N]; // 最小前缀和数组
// 检查是否存在长度≥L的子段,平均数≥mid
bool check(double mid) {
S[0] = 0;
for (int i = 1; i <= n; ++i) {
S[i] = S[i-1] + a[i] - mid; // 计算前缀和,每个元素减去mid
}
min_S[0] = 0;
for (int i = 1; i <= n; ++i) {
min_S[i] = min(min_S[i-1], S[i]); // 维护最小前缀和
}
for (int i = L; i <= n; ++i) {
if (S[i] - min_S[i - L] >= 0) { // 检查是否存在满足条件的子段
return true;
}
}
return false;
}
int main() {
scanf("%d %d", &n, &L);
double left = 0, right = 0;
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
if (a[i] > right) {
right = a[i]; // 右边界初始化为序列最大值
}
}
double eps = 1e-5; // 设置二分精度
while (right - left > eps) {
double mid = (left + right) / 2;
if (check(mid)) {
left = mid; // 可以更大,调整左边界
} else {
right = mid; // 需要更小,调整右边界
}
}
printf("%d\n", (int)(right * 1000)); // 输出平均数的1000倍
return 0;
}
数列分段 II
描述
对于给定的一个长度为 N 的正整数数列 A ,现要将其分成 M 段,并要求每段连续,且每段和的最大值最小。
例如,将数列 4 2 4 5 1 要分成 3 段:
若分为 [4 2][4 5][1],各段的和分别为 6,9,1 ,和的最大值为 9;
若分为 [4][2 4][5 1],各段的和分别为 4,6,6 ,和的最大值为 6;
并且无论如何分段,最大值不会小于 6。
所以可以得到要将数列 4 2 4 5 1 要分成 3 段,每段和的最大值最小为 6 。
输入描述
第 1 行包含两个正整数 N,M;
第 2 行包含 N 个空格隔开的非负整数 A__i,含义如题目所述。
输出描述
仅包含一个正整数,即每段和最大值最小为多少。
用例输入 1
5 3
4 2 4 5 1
用例输出 1
6
提示
数据范围与提示
对于20%的数据,有_N_≤10;
对于40%的数据,有_N_≤1000;
对于100%的数据,有_N_≤1e5,M_≤_N,_Ai_之和不超过1e9。
#include<iostream>
const int N = 1e6+5;
using namespace std;
int n,m,a[N];
bool judge(int x) {
int sum=0,group=1;
for(int i=1; i<=n; i++) {
sum+=a[i];
if(sum>x) {
sum=a[i];
group++;
}
}
if(group<=m)
return true;
else
return false;
}
int main() {
int left=0,right=0;
scanf("%d%d",&n,&m);
for(int i=1; i<=n; i++) {
scanf("%d",&a[i]);
left=max(left,a[i]);
right+=a[i];
}
while(left+1<right) {
int mid=(left+right)/2;
if(judge(mid))
right=mid;
else
left=mid;
}
if(judge(left))
printf("%d\n",left);
else
printf("%d\n",right);
return 0;
}
真题测试
完善程序 (单选题 ,每小题3分,共30分)
切割绳子
有 n 条绳子,每条绳子的长度已知且均为正整数。绳子可以以任意正整数长度切割,但不可以连接。现在要从这些绳子中切割出 m条长度相同的绳段,求绳段的最大长度是多少。(第一、二空 2.5 分,其余 3分)
输入:第一行是一个不超过 100的正整数 n,第二行是 n个不超过 10^6的正整数,表示每条绳子的长度,第三行是一个不超过 10^8的正整数 m。
输出:绳段的最大长度,若无法切割,输出 Failed
#include<iostream>
using namespace std;
int n, m, i, lbound, ubound, mid, count;
int len[100]; // 绳子长度
int main()
{
cin >> n;
count = 0;
for (i = 0; i < n; i++)
{
cin >> len[i];
①;
}
cin >> m;
if (②)
{
cout << "Failed" << endl;
return 0;
}
lbound = 1;
ubound = 1000000;
while (③)
{
mid = ④;
count = 0;
for (i = 0; i < n; i++)
⑤;
if (count < m)
ubound = mid - 1;
else
lbound = mid;
}
cout << lbound << endl;
return 0;
}
1 ①处应填( )
2 ②处应填( )
3 ③处应填( )
4 ④处应填( )
5 ⑤处应填( )
2 相关知识点
二分答案
二分答案顾名思义,它用二分的方法枚举答案,并且枚举时判断这个答案是否可行
直接对答案进行枚举查找,接着判断答案是否合法。如果合法,就将答案二分进一步靠近,如果不合法,就接着二分缩小判断。这样就可以大大的减少时间。
二分中有时可以得可行得答案,但不是最大的,继续向右靠近,求出最大值
int ans = 1;
int l = 1,r = 100000;//在1~100000之间的整数枚举
while(l <= r){
int m = l + (r - l) / 2;
if(check(m)){//满足 则进行向右缩小范围 看看有没有更大的
ans = m;//可能多次赋值 最后一定是可能的最大值
l = m + 1;
}else{//不满足缩小边长 向左缩小范围 用更小边长继续尝试
r = m - 1;
}
}
二分查找中间值
/* 向右逼近,如果找到满足条件的数,会继续向右找更大的数,让循环结束
mid=(left+right)/2 left和right都接近最大值时,可能溢出可以使用下面写法替换
mid=left + (right-left) / 2;
可以求满足条件的最大值
*/
/* 向左逼近,如果找到满足条件的数,会继续向左找更小的数,让循环结束
mid=(left+right+1)/2 left和right都接近最大值时,可能溢出可以使用下面写法替换
mid=left + (right-left+1) / 2;
可以求满足条件的最小值
*/
二分找边界
//左闭右闭 while left right 最终left=right+1
while(left<=right) left = mid + 1; right =mid-1;
//左闭右开 while left right 最终left=right
while(left<right) left = mid + 1; right =mid;
//左开右闭 while left right 最终left=right
while(left<right) left=mid; right=mid-1;
//左开右开 while left right 最终left=right-1
while(left+1<right) left=mid; right=mid;
二分查找时间复杂度
二分查找每次都缩小或扩大为原来的一半,所以也是Olog(n)
3 思路分析
每个棍子长度不超过10^6,且棍子切割必须为整数,因此通过二分的方法在1~ 10^6之间寻找答案
找到1个可能的棍子的长度后,计算n个棍子可以切分棍子的总数
如果总数<m,则切分不够,继续缩小棍子的长度,来切分更多的棍子
直到切分的长度大于等于m
例如
输入
3
4 6 12
7
范围缩小到 lbound=1,ubound=10时
此时mid=(1+10+1)/2=6,使用长度为6进行切分时,3个棍子分别切分为0+1+2=3不能满足m=7
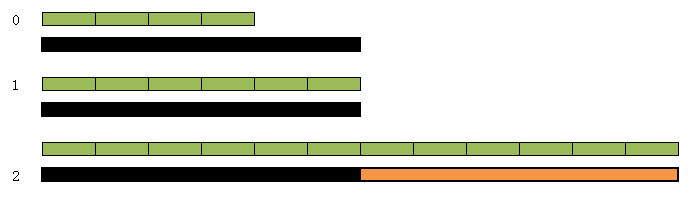
ubound=mid-1=6-1=5
此时mid=(1+5+1)/2=3,使用长度为3进行切分时,3个棍子分别切分为1+2+4=7满足m=7
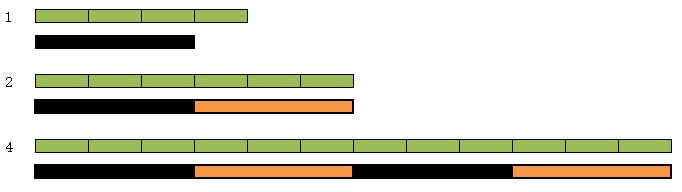
1 ①处应填( count=count+len[i] )
分析
考虑一种情况,先把棍子长度加起来,如果切成最小单位,每个棍子长度为1
这些棍子的总数比m还小,则无法切割
count=count+len[i] 可以看作把所有最小长度为1的棍子都加起来
2 ②处应填( count<m )
分析
考虑一种情况,先把棍子长度加起来,如果切成最小单位,每个棍子长度为1
这些棍子的总数比m还小,则无法切割
count 可以看作把所有最小长度为1的棍子都加起来,如果还不到m个棍子,则无法切割
3 ③处应填( lbound<ubound )
分析
根据如下二分找边界可知, lbound<ubound
//左开右闭 while left right 最终left=right
while(left<right) left=mid; right=mid-1;
4 ④处应填( (lbound+ubound+1)/2 )
分析
根据如下二分找中间值可知, 当特殊情况左边界值不会增加, (lbound+ubound)/2的值不变,会进入死循环
(lbound+ubound)/2会使得左边界+1,结束循环
28 if (count < m)
29 ubound = mid - 1;
30 else
31 lbound = mid;
5 ⑤处应填( count+=len[i]/mid )
分析
二分找出一个棍子长度mid,计算所有棍子,按mid长度可以切分的棍子数量
26 for (i = 0; i < n; i++)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号