Luogu 1979 NOIP 2013 华容道(搜索,最短路径)
Luogu 1979 NOIP 2013 华容道(搜索,最短路径)
Description
小 B 最近迷上了华容道,可是他总是要花很长的时间才能完成一次。于是,他想到用编程来完成华容道:给定一种局面, 华容道是否根本就无法完成,如果能完成, 最少需要多少时间。
小 B 玩的华容道与经典的华容道游戏略有不同,游戏规则是这样的:
在一个 nm 棋盘上有 nm 个格子,其中有且只有一个格子是空白的,其余 nm-1个格子上每个格子上有一个棋子,每个棋子的大小都是 11 的;
有些棋子是固定的,有些棋子则是可以移动的;
任何与空白的格子相邻(有公共的边)的格子上的棋子都可以移动到空白格子上。
游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。
给定一个棋盘,游戏可以玩 q 次,当然,每次棋盘上固定的格子是不会变的, 但是棋盘上空白的格子的初始位置、 指定的可移动的棋子的初始位置和目标位置却可能不同。第 i 次
玩的时候, 空白的格子在第 EXi 行第 EYi列,指定的可移动棋子的初始位置为第 SXi 行第 SYi列,目标位置为第 TXi 行第 TYi 列。
假设小 B 每秒钟能进行一次移动棋子的操作,而其他操作的时间都可以忽略不计。请你告诉小 B 每一次游戏所需要的最少时间,或者告诉他不可能完成游戏。
Input
第一行有 3 个整数,每两个整数之间用一个空格隔开,依次表示 n、m 和 q;
接下来的 n 行描述一个 n*m 的棋盘,每行有 m 个整数,每两个整数之间用一个空格隔开,每个整数描述棋盘上一个格子的状态,0 表示该格子上的棋子是固定的,1 表示该格子上的棋子可以移动或者该格子是空白的。接下来的 q 行,每行包含 6 个整数依次是 EXi、EYi、SXi、SYi、TXi、TYi,每两个整数之间用一个空格隔开,表示每次游戏空白格子的位置,指定棋子的初始位置和目标位置。
Output
输出有 q 行,每行包含 1 个整数,表示每次游戏所需要的最少时间,如果某次游戏无法完成目标则输出−1。
Sample Input
3 4 2
0 1 1 1
0 1 1 0
0 1 0 0
3 2 1 2 2 2
1 2 2 2 3 2
Sample Output
2
-1
Http
Luogu:https://www.luogu.org/problem/show?pid=1979
Source
搜索,最短路径
解决思路
首先考虑搜索。我们发现每一次,我们移动空格,同时可能移动我们指定的棋子,那么一直这么移,直到将指定棋子移动到目标格。这样做能获得70~90分。
然后我们想如何简化。贪心的想一想,首先肯定先得让空格移动到指定的棋子旁边,因为这样才能让指定的棋子移动。其次,当空格移动到指定的棋子旁边后,我们最好不让它再离开指定的棋子,除非是要让开一个位置或是其他的特殊操作,但最后总还是要回到指定棋子旁边。
这时我们发现,我们把原来搜索时一步移动空格一格变成了一步让空格从指定格的某一方向变到另一方向。就像下面这样
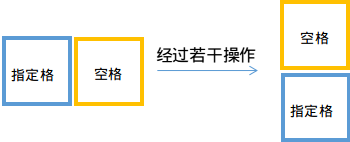
所以我们可以预处理出这个东西,即\(Skip[i][j][f1][f2]\),代表的是格子\([i][j]\)时,空格在方向\(f1\),要把空格移到方向\(f2\)并与指定格交换的步数,相当于先把空格移到指定的方向的步数再+1。
为了方便叙述,我们规定:1上,2下,3左,4右
这个怎么求呢?不用想什么复杂的算法,4重循环枚举\(Skip\)的四个参数,然后直接从\(f1\)方向上的那个格子开始\(bfs\),最后返回\(f2\)方向上格子的步数。但需要注意的是,我们在\(bfs\)的时候要把指定格(即蓝色的格子)固定下来,因为不能让他和空格交换,导致混乱,所以我们可以把指定格置为0(即与不能走的格子一样),\(bfs\)完后再置回来,这样就可以保证指定格不会在移动空格的时候动,只要最后再把空格和指定格交换即可。
这时我们再来看,我们把题目转换成了一个类似于图论的东西,图中的点就是\((i,j,f)\)其中\(f\)代表方向,\((i,j)\)代表原矩阵中的第\(i\)行第\(j\)列,而每一个\(Skip[i][j][f1][f2]\)则代表的是一条边,从\((i,j,f1)\)到\((i,j,f3)\),其中\(f3\)代表\(f2\)的反方向。
为什么是反方向呢?因为

所以我们最后在这张图上进行一次最短路算法,这里选用比较好实现的SPFA。
总结一下,这道题的流程就是:
1.输入数据,并预处理出\(Skip[i][j][f1][f2]\)
2.对于每一组询问:
(1).先让空白格移动到指定格的初始位置的周围四个格子
(2).将空白格与指定格捆绑行动,求解类最短路
另外需要注意的是,可能出现初始位置与目标位置一致的情况,这时直接输出0。
代码
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
#define mem(Arr,x) memset(Arr,x,sizeof(Arr))
const int maxMat=40;
const int maxF=5;
const int meminf=2139062143;//这个值与memset(Arr,127,sizeof(Arr))中Arr的每一个数的值一致
const int ff[5]={0,2,1,4,3};//ff[i]表示i的相反方向
class Pos//位置
{
public:
int x,y;
Pos()
{
return;
}
Pos(int a,int b)
{
x=a;
y=b;
}
};
class Queue_Data
{
public:
int x,y,f;
};
int n,m;
int Mat[maxMat][maxMat];
Pos F[maxF];
int Skip[maxMat][maxMat][maxF][maxF];
int Dist[maxMat][maxMat][maxF];//求解最短距离
bool vis[maxMat][maxMat][maxF];
queue<Queue_Data> Q;
Pos operator + (Pos A,Pos B);
Queue_Data operator + (Queue_Data A,Pos B);
void init();
int Bfs(Pos st,Pos ed);//从位置st走到位置ed的步数
int main()
{
int qus;//询问个数
scanf("%d%d%d",&n,&m,&qus);
for (int i=1;i<=n;i++)
for (int j=1;j<=m;j++)
scanf("%d",&Mat[i][j]);
init();//初始化Skip
while (qus--)//处理询问
{
int Epx,Epy,Stx,Sty,Glx,Gly;
scanf("%d%d%d%d%d%d",&Epx,&Epy,&Stx,&Sty,&Glx,&Gly);
if ((Mat[Stx][Sty]==0)||(Mat[Glx][Gly]==0))//当初始或目标位置本身不可走时,直接输出-1
{
printf("-1\n");
continue;
}
if ((Stx==Glx)&&(Sty==Gly))//当初始与目标位置相同时,直接输出0
{
printf("0\n");
continue;
}
while (!Q.empty())//初始化
Q.pop();
mem(Dist,127);
mem(vis,0);
//求出将空白格移动到指定格初始位置四周的步数,并将其中可行的放入队列
Mat[Stx][Sty]=0;//因为要求出空白格移动的步数,所以这时初始位置不能动,先置为0表示不可走
Pos init=(Pos){Stx,Sty};
for (int i=1;i<=4;i++)
{
Pos v=init+F[i];//枚举初始位置的四周
Dist[Stx][Sty][i]=Bfs((Pos){Epx,Epy},v);//Bfs求解从空格走到的距离
if (Dist[Stx][Sty][i]!=meminf)
Q.push((Queue_Data){Stx,Sty,i});//如果可行,放入队列
}
Mat[Stx][Sty]=1;//处理完后重新置为1
//求解最短路
while (!Q.empty())
{
Queue_Data u=Q.front();
Q.pop();
vis[u.x][u.y][u.f]=0;
for (int i=1;i<=4;i++)//枚举四个方向
{
Queue_Data v=u+F[i];
v.f=ff[i];//注意这里最后的空格方向要变为方向i的反方向
if (Dist[v.x][v.y][v.f]>Dist[u.x][u.y][u.f]+Skip[u.x][u.y][u.f][i])
{
Dist[v.x][v.y][v.f]=Dist[u.x][u.y][u.f]+Skip[u.x][u.y][u.f][i];
if (vis[v.x][v.y][v.f]==0)
{
Q.push(v);
vis[v.x][v.y][v.f]=1;
}
}
}
}
int Ans=meminf;
for (int i=1;i<=4;i++)
Ans=min(Ans,Dist[Glx][Gly][i]);//找出最小值
if (Ans==meminf)
Ans=-1;
printf("%d\n",Ans);
}
return 0;
}
Pos operator + (Pos A,Pos B)//为了方便向四周移动,重载位置的加法
{
return (Pos){A.x+B.x,A.y+B.y};
}
Queue_Data operator + (Queue_Data A,Pos B)//同上
{
return (Queue_Data){A.x+B.x,A.y+B.y,A.f};
}
void init()
{
F[1]=(Pos){-1,0};//这个F就是在枚举向哪个方向移动时用的
F[2]=(Pos){1,0};
F[3]=(Pos){0,-1};
F[4]=(Pos){0,1};
mem(Skip,127);
for (int i=1;i<=n;i++)//四重循环枚举(i,j),空格所在方向f1,要将(i,j)移动去的方向f2
for (int j=1;j<=m;j++)
{
if (Mat[i][j]==0)//若(i,j)本身不可走则不进行操作
continue;
Mat[i][j]=0;//因为不能在移动空格的时候使(i,j)被移动,所以先置为不能走
Pos now(i,j);
for (int f1=1;f1<=4;f1++)//枚举方向
for (int f2=1;f2<=4;f2++)
{
if (f1>f2)//空格在f1,当前格走到f2和空格在f2,当前格走到f1的步数是一样的
{
Skip[i][j][f1][f2]=Skip[i][j][f2][f1];
continue;
}
Skip[i][j][f1][f2]=Bfs(now+F[f1],now+F[f2])+1;//Bfs求解
}
Mat[i][j]=1;//置回来
}
return;
}
int Bfs(Pos st,Pos ed)//求解从st走到ed的步数
{
if ((Mat[st.x][st.y]==0)||(Mat[ed.x][ed.y]==0))//当这两个点中有任意一个不可走时,直接返回无穷大
return meminf;
//各种初始化
queue<Pos> Q;
while (!Q.empty())
Q.pop();
bool vis[maxMat][maxMat];
int Dist[maxMat][maxMat];
mem(vis,0);
mem(Dist,127);
//将st放入队列
Q.push(st);
vis[st.x][st.y]=1;
Dist[st.x][st.y]=0;
do
{
Pos u=Q.front();
Q.pop();
for (int i=1;i<=4;i++)//枚举向四个方向走
{
Pos v=u+F[i];
if ((Mat[v.x][v.y]==0)||(vis[v.x][v.y]==1))
continue;
vis[v.x][v.y]=1;
Dist[v.x][v.y]=Dist[u.x][u.y]+1;
Q.push(v);
}
}
while (!Q.empty());
return Dist[ed.x][ed.y];//返回步数
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号