集训-题解合集

将军的恩情(sunlight)

首先可以考虑到一个非常朴素的 \(\mathrm{dp}\)，定义 \(f_{i,x,y}\) 表示前 \(i\) 轮有 \(x\) 个 \(A\) 向日葵，\(y\) 个 \(B\) 向日葵的最大阳光数。因为在向日葵个数的限定下显然目前阳光越多越优，因此是有正确性的，分当前这一轮的操作转移即可，可以做到 \(O(n^3)\)，赛时止步于此，因为注意到这样子设计状态难以优化。

于是转变一下状态定义，定义 \(f_{i,j}\) 表示前 \(i\) 轮种植的向日葵到第 \(i\) 轮每轮会获得 \(j\) 的收益的最大阳光数。相当于在原来的 \(\mathrm{dp}\) 中令 \(j=q_1\cdot x+q_2\cdot y\)。转移就是：

\[f_{i+1,j}\leftarrow f_{i,j}+j \\ f_{i+1,j+q_1}\leftarrow f_{i,j}-p_1+(j+q_1),\quad\texttt{if }f_{i,j}\ge p_1 \\ f_{i+1,j+q_2}\leftarrow f_{i,j}-p_2+(j+q_2),\quad\texttt{if } f_{i,j}\ge p_2 \\ f_{i+1,j+q_1+q_2}\leftarrow f_{i,j}-p_1-p_2+(j+q_1+q_2),\quad \texttt{if }f_{i,j}\ge p_1+p_2 \]

这样设计就将 \(x,y\) 两维压成了 \(j\) 一维。此时状态数就是 \(O(n\times n(q_1+q_2))=O(n^2q)\)，需要进一步优化。

开始有意思了。我们声称原来的 \(\mathrm{dp}\) 不好解决的部分就是需要条件的限定，什么时候可以直接去掉这些限制？注意到，如果 \(j\ge p_1+p_2\)，也即每次的收益都足够支付两种向日葵都购买的费用，那么就不需要考虑不够钱购买的问题了。如果满足了这一点，那么可以直接用一个简单的贪心解决问题，拆个贡献，在每一轮中看看种下的向日葵能不能在最后造成正的贡献，如果可以就直接种。因此 \(\mathrm{dp}\) 的 \(j\) 一维只需要最大跑到 \(p_1+p_2\)，记 \(m=p_1+q_1\)，状态数压到了 \(O(n(p_1+p_2))=O(nm)\)。仍然不够优。

顺着刚刚的思路，考虑继续压缩 \(i\) 的范围。由于收益 \(q\ge 1\)，所以在 \(p\) 轮之后就可以得到购买一个向日葵的钱，购买之后，收益就 \(\ge 2\)，所以在 \(\frac{p}{2}\) 轮后又可以购买一个向日葵，并且在购买了 \(p_1+p_2=m\) 个向日葵之后，每一轮的收益都足够支付两种向日葵都购买的费用，因此总共只需要 \(m+\frac{m}{2}+\frac{m}{3}+\dots=O(m\ln m)\) 轮之后，就可以用之前的贪心来解决了。因此 \(i\) 这一位也被压到了 \(O(m\ln m)\) 的级别，总状态数就是 \(O(m^2\ln m)\) 了。

---

发喷山火(volcano)

解题报告

---

计数

简要题意： 求满足 \(a_i\le b_i\le R\) 的单调不上升序列 \(b\) 的方案数，\(n\le 5\times 10^3,a_i\le R\le 10^9\)。

解法：

先考虑一个很朴素的 \(\mathrm{dp}\)，定义 \(F_i(x)\) 表示后 \(i\) 个数已经填好，\(b_i=x\) 的方案数。得到转移：

\[F_i(x)=\sum_{k=a_{i+1}}^{x} F_{i+1}(k) \]

由于 \(b_i\) 的值域是 \(R\)，所以状态数和时间复杂度为 \(O(nR)\)，无法通过。

先来挖掘一下这个多项式的性质。我们声称 \(F_i(x)\) 是一个关于 \(x\) 的 \(n-i\) 次多项式。感性理解就是这个限制可以看做格路计数，限定不能碰到 \(n\) 个点。这个的容斥 \(\mathrm{dp}\) 表示出来的式子是 \(n-i\) 次的多项式。

于是考虑用二项式系数基来表示出 \(F_i(x)\)，得到： \(F_i(x)=\displaystyle\sum_{k=0}^{n-i}c_{i,k}\dbinom{x}{k}\)。

接着来推导一下 \(F_i(x)\) 的转移：

\[\begin{align} F_i(x) &= \sum_{j=a_{i+1}}^{x} F_{i+1}(j) \\ &= \sum_{j=a_{i+1}}^{x} \sum_{k=0}^{n-i-1} c_{i+1,k}\binom{j}{k} \\ &= \sum_{k=0}^{n-i-1} c_{i+1,k} \sum_{j=a_{i+1}}^{x}\binom{j}{k} \\ &= \sum_{k=0}^{n-i-1} c_{i+1,k} \left[\binom{x+1}{k+1}-\binom{a_{i+1}}{k+1}\right] \\ &= \sum_{k=0}^{n-i-1} c_{i+1,k} \left[\binom{x}{k}+\binom{x}{k+1}-\binom{a_{i+1}}{k+1}\right] \\ \end{align} \]

重新审视我们要求的新系数 \(c_{i,k}\)，其贡献到的系数是 \(\binom{x}{k}\)，因此我们可以找到系数为 \(\binom{x}{k}\) 的项，即 \(c_{i+1,k}\dbinom{x}{k},c_{i+1,k-1}\dbinom{x}{k}\)，因此 \(c_{i,k}\leftarrow c_{i+1,k}+c_{i+1,k-1}\)。但是还有 \(-\displaystyle\sum_{k=0}^{n-i-1}c_{i+1,k}\dbinom{a_{i+1}}{k+1}\) 这一项不好处理，不过注意到 \(c_{i,0}\) 的贡献系数是 \(1\)，所以可以直接将这个贡献加到 \(c_{i,0}\) 处即可。于是可以做到 \(O(n)\) 转移一层系数。那么答案就是 \(F_{0}(R)\)，可以 \(O(n^2)\) 推出 \(c_0\)，带入即可求出答案。

谁问我了

---

序列

很具有启发性的题目，加深了对处理异或最值问题的理解。

算法1： 显然询问可以贪心处理，往右扩展时 \(\min\) 式子递减，限制不断变松，所以在最靠前的能划分处划分即可，需要动态插入维护区间 \(\displaystyle\min_{i\ne j}\set{a_i\oplus a_j}\)，很直观的想法就是用 \(\texttt{Trie}\)，时间复杂度 \(O(qn\log V)\)，无法通过。

算法2：考虑优化，有性质：\(a<b<c\Rightarrow \min(a\oplus b,b\oplus c)<(a\oplus c)\)，证明考虑拉出来最高位，是简单的。这个相当于告诉我们异或最小值只会在值域上相邻两数上取到，于是可以开一个 (multi)set，每次插入时用前驱后继更新答案，可以做到 \(O(qn\log n)\)，由于大肠熟无法通过。

算法3： 求出异或最小值看来不能优于 \(\mathrm{polylog}\) 了。但我们的目的只是判断 \(\min\le w\)，而非求出 \(\min\) 的最小值。令 \(2^k\) 为 \(w\) 的最高位 ，考虑将 \(a_i\) 按照 \(\left\lfloor\dfrac{a_i}{2^{k+1}}\right\rfloor\)，换言之，将比 \(w\) 更高的位拉出来分组。这样分有什么性质？我们发现，在不满足条件，即 \(\min>w\) 时，每一组中最多有两个数，证明考虑抽屉原理，如果有多于两个数那么肯定会有两个数第 \(k\) 位相等，比 \(k\) 高的位由于分到同一个组所以会消掉，第 \(k\) 位相等也会消掉，这样异或完就一定小于 \(w\) 了。因此可以扫的时候往组中加数，有组爆了或是放进去之后异或值满足要求就可以。时间复杂度 \(O(qn)\)，可以通过。

---

走路赚钱

两个维度的限制不好处理，考虑固定住 \(x\) 时求出 \(y\) 的范围。

如果能由 \(\texttt{X}\) 公司的 \(i\) 限制贡献过来，那么相当于在 \(x+y=w_i\) 时有 \(x\ge k_i\)，即 \(x\ge k_i\) 时需要 \(y\le w_i-k_i\)，由于 \(x,y\) 只会增，所以将贡献钦定在 \(x=k_i\) 处，即 \(x=k_i\) 时如果 \(y\le w_i-k_i\) 就有 \(v_i\) 贡献。

如果能由 \(\texttt{Y}\) 公司的 \(i\) 限制贡献过来，那么相当于在 \(x+y=w_i\) 时有 \(y\ge k_i\)，即 \(y\ge k_i\) 时需要 \(x\le w_i-k_i\)，同样由于 \(x,y\) 只增，所以在 \(x=w_i-k_i\) 时若 \(y\ge k_i\) 就算上 \(v_i\) 贡献。

那么就可以简单设计出一个 \(\mathrm{dp}\)：\(f_{i,j}\) 表示目前走到 \(x=i,y=j\) 位置的贡献最大值，那么我们的策略显然是在能吃到贡献的情况下尽量压低 \(j\)，得到：

\[\begin{aligned} f_{i,j}&\leftarrow f_{i-1,j}+[j\le l_k]\times v_k \\ f_{i,j}&\leftarrow f_{i-1,j}+[j\ge r_k]\times v_k \\ f_{i,r_k}&\leftarrow \max_{h<r_k}f_{i-1,h}+v_k \end{aligned} \]

直接扫描线用线段树优化即可，时间复杂度 \(O(n\log n)\)。

---

ending

感谢铁一米孝子教导

注意到 \(c_{\min\left(|i-p_i|,m\right)}\)，故考虑 \(c_m=0\)，即限定 \(|i-p_i|<m\) 的情况。排列有位置、值域两种角度的 \(\mathrm{dp}\) 方式，考虑从值域角度 \(\mathrm{dp}\)，那么对于数 \(i\)，只能放到 \([i-m+1,i+m-1]\)，并且由于 \(m\) 很小，我们可以直接将其压到一个状态中，定义 \(f_{i,msk}\) 表示放好了 \([1,i]\) 的数，并且 \([i-m+1,i+m-1]\) 填数的状态为 \(msk\) 的贡献和。转移就是一个类似状态右移接上一个位的过程。

但是如果 \(c_m\) 非零，那么需要计算 \(|i-p_i|\ge m\) 的贡献，我们称 \(|i-p_i|\ge m\) 是非法的。于是可以在 \(\mathrm{dp}\) 时空出一些数不填作为非法的，再记录一维 \(k\) 表示目前有多少个数填了。那么就有 \((n-k)\) 个非法位置，总计 \((n-k)!\) 种排列，每个的贡献是 \(c_m\)，总贡献就是 \((n-k)!\times {c_m}^{(n-k)}\)？错了，因为不难发现这样会算重，考虑这样一种情况：

\[\begin{aligned} id:&\texttt{1 2 3 4 5} \\ p:&\texttt{3 4 5 1 2} \\ c:&\texttt{2 2 2 m m} \\ \end{aligned} \]

其中 \(m=3\)。那么后面的 \((4,1),(5,2)\) 就是非法的。但是按照我们的算法，就会计算：

\[\begin{aligned} id:&\texttt{1 2 3 4 5} \\ p:&\texttt{3 4 5 2 1} \\ c:&\texttt{2 2 2 2 m} \\ \end{aligned} \]

注意到此时 \((4,2)\) 就变得合法了，算重了。

如何解决？考虑容斥，假设我们要计算合法集合 \(S\) 的实际贡献。回顾一下，原来的问题出在非法集合内部的交换会导致某些非法位置变成合法位置。如果我们将其看作合法集合的扩张，就变成了一个超集容斥的形式，考虑在 \(\texttt{2 2 2 2 m}\) 处减掉 \(\texttt{2 2 2 m m}\) 算重的部分。如何做到这样，考察两部分的变化：

\[\begin{aligned} &c_2\times c_2\times c_2\times c_2\times c_m \\ - &c_{2}\times c_2\times c_2\times c_m\times c_m \end{aligned} \]

注意到会减去 \(\texttt{sth.}\times (c_2-c_m)\)，于是我们大胆猜测正确的贡献应该为 \(\displaystyle\prod (c_i-c_m)\)，证明考虑展开这个式子：

\[\prod(c_i-c_m)=\sum_{S} \left[\left(\prod_{i\in S}c_i\right)\times (-c_m)^{|U|-|S|}\right] \]

感觉上就是符合容斥的，并且这个贡献实际上把容斥系数也算上了。

因此我们做出的更改很简单，\(\mathrm{dp}\) 部分原来的贡献 \(c_i\) 变成 \((c_i-c_m)\) 转移即可。

时间复杂度 \(O(n^2 2^{2m-1}m)\)。

---

换乘旅行

对于图论问题，可以考虑从特殊的图形态开始考虑。分析一下没有环的情况，此时从每个点出发一定不会再走回来，这意味着每一次都会走 \(d_{i,1}\)，可以用记忆化搜索解决。如果出现环，即从某个点 \(u\) 绕一圈又回来，那么可以看做将环上所有点的第一辆车扔掉然后继续走，相当于这个环被删掉了，因此我们可以每次找到一个环然后删掉。这样最后的图中一定没有环，用上述的记忆化搜索解决即可。

删环考虑类似 \(\texttt{Tarjan}\) 求强连通分量的做法，搜索时如果碰到入栈节点则将这个环找出来并删掉，每个点最多作为环上节点被删掉 \(O(\mathrm{deg})\) 次，因此总时间复杂度 \(O(n+m)\)。

---

C. Lead to shine more

注意到 \(\mathrm{popc}(S)\le 64\)，考虑进行一个拆开的操作，分为 \(x\) 的高 \(6\) 位 \(hi\) 和低 \(6\) 位 \(low\)，即 \(x=2^6\cdot hi+low\)。我们发现此时 \(+\mathrm{popc}(S)\) 最多只会使 \(hi\) 增加 \(1\)。于是我们尝试定义 \(f(i,j)\) 表示 \(\mathrm{popc}(hi)=i,\space low=j\) 时，要使得 \(hi\) 增加 \(1\) 所需要的新 \(low\) 和操作次数，这个可以直接暴力增加 \(j\leftarrow j+\mathrm{popc}(j)+i\) 计算得到。但是查询时每次跳 \(f(i,j)\) 增加就太慢了，考虑每次跳完一位，即假设目标 \(n=\underbrace{100101\dots}_{hi} [low]\)，我们直接按从高到低的顺序跳满 \(hi\) 的每个 \(1\)，即先跳 \(100000\dots\)，然后跳 \(100\dots\) 跳到 \(100100\dots\)，由于每次对 \(hi\) 的增量是 \(1\) 所以这个是可以做到的。如何做这个过程？考虑类似倍增的 \(\mathrm{dp}\)，定义 \(f_{k,i,j},g_{k,i,j}\) 分别表示要使得第 \(k\) 位第一次进位，即达成 \(\underbrace{100\dots}_{k} [low]\) 形式，且初始时 \(\mathrm{popc}(hi)=i,\space low=j\) 的新 \(low\) 和最小步数。初始时有 \(f_{0,i,j}=f(i,j)\)，对于第 \(k\) 位，其可以由 \(k-1\) 位进位两次得到，此处不再赘述，得到

\[f_{k,i,j}=f_{k-1,i+1,f_{k-1,i,j}} \\ g_{k,i,j}=g_{k-1,i,j}+g_{k-1,i+1,f_{k-1,i,j}} \]

询问直接跳即可。时间复杂度为 \(O(\log^3 V+Q\log V)\)。

---

利物浦集合

简要题意：

记 \(f(n,m,k)\) 表示满足：

1. 长度为 \(n\)，所有数在 \([0,2^m)\) 之间，且任意数出现次数都不超过 \(k\)。
2. 异或和为 \(0\)

的可重集 \(a\) 数量。

给定 \(n_1,m_1,k_1\)，求 \(f(n_1,m_1,k_1)\)。以及给定 \(n_2,m_2\)，求出所有 \(f(n_2,m_2,i)\)。

\(n_1\le 10^7,n_2\le 10^6,m_1,m_2\le 23\)。

解法：

异或和为 \(0\) 比较难处理，不过限制1相对来说就比较好解决，考虑容斥，我们可以枚举出现次数爆掉 \(k\) 的数种类 \(i\)，那么钦定有至少 \(i\) 个位置爆到至少 \((k+1)\) 之后随便可重集，简单组合数即可。记这个方案数为 \(S\)，则有

\[S=\sum_{i=0}^{\left\lfloor\frac{n}{k+1}\right\rfloor} (-1)^i \binom{2^m}{i}\binom{n-i(k+1)+2^m-1}{2^m-1} \]

解释一下，容斥系数 \((-1)^i\) 是因为这本质是求并集，选出这 \(i\) 个数后，钦定 \(i\) 个数爆上界的方法就是让这些数至少选 \((k+1)\) 个，选完剩下 \(n-i(k+1)\) 个数，放 \(2^m\) 种数，可重集计数是一个插板。

接下来要解决异或和为 \(0\) 的问题了。定义 \(f(x)\) 表示异或和为 \(x\) 的合法方案数，答案就是 \(f(0)\)。首先有神秘观察，所有非 \(0\) 的 \(x\) 对应的 \(f(x)\) 都相等，即 \(f(1)=\dots=f(2^m-1)\)。

那么 \(n\) 为奇数的情况就直接得到了解决，因为一个异或和为 \(x\) 的可重集，每个数都异或上 \(x\) 那么整体异或和就变成了 \(0\)，也即每个异或和为 \(0\) 的可重集都被计算了 \(2^m\) 次，因此 \(n\) 为奇数答案就是 \(\dfrac{S}{2^m}\)。

若 \(n\) 为偶数，需要找到一个方便计算的形式。注意到 \(msk=2^m-1\) 是一个性质比较多的数，因而我们尝试用 \(f(msk)\) 和 \(f(0)\) 扯上关系。考虑定义 \(T=f(0)-f(msk)\)，结合上 \(S=\sum\limits_x f(x)=f(0)+(2^m-1)f(msk)\)，可以解得最终答案就是 \(\dfrac{S+T(2^m-1)}{2^m}\)，考虑如何求 \(T\)。

挖掘 \(msk\) 的性质，考虑将 \((i,msk\oplus i)\) 分为一组，即 \((0,2^m-1),\dots,(2^{m-1}-1,2^{m-1})\) 共 \(2^{m-1}\) 个二元组，这样二元组不重不漏地覆盖了 \([0,2^m)\) 的所有数。假设 \(i\) 被选进可重集的次数为 \(cx_i\)，\((msk\oplus i)\) 被选进可重集的次数为 \(cy_i\)，则可以表示出这个二元组在整体上的异或和贡献为 \((i[cx_i\bmod 2])\oplus ((msk\oplus i)[cy_i\bmod 2])\)，若 \(cx_i\not\equiv cy_i\pmod 2\)，则如果我们交换两者的出现次数，两边都发生反转，相当于整体异或 \(i\oplus (msk\oplus i)=msk\)，则总异或和变为 \(msk\oplus msk=0\)。这说明了，对于任意一个存在 \(cx_i\not\equiv cy_i\pmod 2\) 且异或和为 \(msk\) 的可重集，我们可以交换其最靠前的非法位置，使其变成一个异或和为 \(0\) 的可重集，换言之，我们在【存在 \(cx_i,cy_i\) 奇偶不同且异或和为 \(msk\) 的可重集】和【一个异或和为 \(0\) 的可重集】之间建立了映射，并且是一一对应的。因此这些存在 \(cx_i,cy_i\) 奇偶不同的可重集在 \(f(0)-f(msk)\) 中被直接抵消掉了。

于是我们发现剩下的可重集中所有 \(cx_i,cy_i\) 都是同奇偶的。再次对这个进行容斥。此处用到生成函数的技巧，定义

\(F,G\) 分别表示奇偶 \(1-1\) 配对 和 \(0-0\) 配对的生成函数，枚举两者分别有多少个，则我们实际上要求的就是：

\[T=[x^n] \sum_{i=0}^{2^{m-1}} (-1)^i F^iG^{2^{m-1}-i}\binom{2^{m-1}}{i} \\ =[x^n] \sum_{i=0}^{2^{m-1}} (-F)^iG^{2^{m-1}-i}\binom{2^{m-1}}{i} \\ =[x^n](G-F)^{2^{m-1}} \]

分类讨论一下 \(F,G\)

• \(k\bmod 2=0\)

  那么枚举和为 \((2i)\)，于是其中一个数可以选 \(a=0,2,4,\dots,(2i)\) 共 \((i+1)\) 种方案，但是另外一个数必须满足 \(\le k\)，因此 \(i>\frac{k}{2}\) 时需要调整一下，得到：\(G=\sum\limits_{2i\le k} (i+1)x^{2i}+\sum\limits_{k<2i\le 2k} (k-i+1) x^{2i}\)。

  同理得到 \(F=\sum\limits_{2i\le k} ix^{2i}+\sum\limits_{k<2i\le 2k} (k-i) x^{2i}\)。

  此时 \(G-F=x^0+x^2+\dots+x^{2k}\)。

  此时 \([x^n](G-F)^{2^{m-1}}\) 的意义是什么？相当于用 \(2^{m-1}\) 个 \(0,2,4,\dots,2k\) 组出和为 \(n\) 的方案数。套用求 \(S\) 时的做法，如果将所有数同消掉一个 \(2\)，就是用 \([0,k]\) 组出和为 \(\frac{n}{2}\)，这个直接就是 \(S\) 的问题本体：

  \[T=\sum_{i=0}^{\left\lfloor\frac{\frac{n}{2}}{k+1}\right\rfloor} (-1)^i \binom{2^{m-1}}{i}\binom{\frac{n}{2}-i(k+1)+2^{m-1}-1}{2^{m-1}-1} \]

• \(k\bmod 2=1\)

  同理得到 \(G-F=x^0+x^2+\dots +x^{k-1}-x^{k+1}-x^{k+3}-\dots -x^{2k}\)。

  这下这下了，有太多部分不好处理。首先可以将每个数都除掉 \(2\)，相当于用 \([0,k]\) 组出和为 \(\frac{n}{2}\)，令 \(t=\frac{k+1}{2}\)，则 \(<t\) 的部分贡献为 \(1\)，\([t,k]\) 的部分贡献为 \(-1\)。

  感性理解就是可以将每个位置拆成两个点，选择一个点表示将其对应的位置钦定 \(>t\)，我们发现这似乎将 \([t,k]\) 的 \(-1\) 贡献也统一到容斥系数中，那么相当于有 \(2^{m-1}\times 2=2^m\) 个数供选择，贡献就是：

\[T=\sum_{i=0}^{\left\lfloor\frac{\frac{n}{2}}{\frac{k+1}{2}}\right\rfloor} (-1)^i\binom{2^m}{i}\binom{\frac{n}{2}-i\frac{(k+1)}{2}+2^{m-1}-1}{2^{m-1}-1} \]

于是似乎解决了，由于对于一个 \(k\) 是 \(O\left(\frac{n}{k}\right)\) 的，总时间复杂度 \(O(n\ln n)\)。

---

gene

简要题意： 你有一个长为 \(2^n\) 的数组，支持：询问子集和、单点加、超集加、子集加。\(n\le 20,Q\le 10^5\)。

先考虑只有单点加的做法。考虑拆高低位的 \(\texttt{Trick}\)，记 \(m=\frac{n}{2}\)，将数拆成高 \(m\) 位 \(S_1\) 和低 \(m\) 位 \(S_2\)，定义 \(W_{i,j}\) 表示 \(S_1=i,\space S_2\subseteq j\) 的权值和，则查询时只需要查询 \(W_{*,S_2}\)，单点加增加 \(W_{S_1,*}\)，这样很巧妙地平衡了时间复杂度，操作都是 \(O(2^m)\) 的。考虑拓展到超集、子集加的情况。

套路地拆一下贡献，考虑修改对询问的贡献。对于超集加，其贡献类似 \(\sum\limits_{T\subseteq S}\sum\limits_{P\subseteq T} w_P=\sum\limits_{P}w_P\sum\limits_{T}[P\subseteq T\subseteq S]=\sum\limits_{P\subseteq S} w_P\times 2^{|S|-|P|}\)，因此一次 \(P\) 处超集加的贡献系数为 \([P\subseteq S]2^{|S|-|P|}\)，注意到这和单点加的贡献形式是相同的，贡献改成 \(2^{-|P|}\times w\) 即可，需要最后乘上 \(2^{|S|}\)。

对于子集加，同样拆出贡献：\(\sum\limits_{T\subseteq S} \sum\limits_{P\supseteq T} w_P=\sum\limits_{P} w_P\sum\limits_{T}[T\subseteq S\wedge T\subseteq P]=\sum\limits_{P} w_P2^{|S\cap P|}\)，需要拆 \(2^{|S\cap P|}\)，注意到 \(2^{|S\cap P|}=2^{|S_1\cap P_1|}\cdot 2^{|S_2\cap P_2|}\)，仿照单点加定义 \(g_{i,j}\) 表示 \(\sum\limits_P\sum\limits_{P_1=i} w\times 2^{|P_2\cap j|}\)，修改时更新 \(g_{P_1,*}\)，只需要枚举 \(j\)，是 \(O(2^m)\) 的，询问时枚举 \(P_1\)，答案就是 \(\sum\limits_{P_1} 2^{|S_1\cap P_1|}g_{P_1,S_2}\)，同样是 \(O(2^m)\) 的。

于是我们在 \(O(Q2^m)\) 的复杂度下解决了问题。

还有一种操作分块的做法，每 \(B\) 个操作分为一块，对于每个询问，暴力处理其所在块前半部分的贡献，这个可以类似前面拆贡献做到 \(O(B)\)，而整块部分考虑每个块求高维前缀和状物，总共需要 \(O(2^n n\times \frac{Q}{B})\)，处理完可以 \(O(1)\) 查询一段，因此总时间复杂度为 \(O(Q(B+\frac{n}{B})+2^n n\frac{Q}{B})=O(Q(B+\frac{2^nn}{B}))\)，平衡一下取 \(B=\sqrt{2^n n}\)，时间复杂度 \(O(Q\sqrt{2^n n})=O(Q2^m\sqrt{n})\)。

---

begin

赛时脑抽了，怎么会是呢？

考虑一个非常直接的 \(\mathrm{dp}\)，令 \(f_{i,0/1}\) 表示考虑前 \(i\) 个数，且 \(T\) 中是否选择了 \(i\) 的方案数。但是我们发现这个虚假了，怎么会是呢？我们只是单纯的记录了 \(T\) 中是否有 \(i\)，但 \(T_i=1\) 并不表示 \({T^{\prime}}_i=0/1\) 都是合法的，所以这个虚假了。那么考虑直接拓成三个状态，令 \(f_{i,0/1/2}\) 表示考虑前 \(i\) 个数，在 \([1,i-1]\) 做完之后，第 \(i\) 个数 【不选合法，选不合法】/ 【选合法，不选不合法】/ 【选或不选都合法】，初值就是 \(f_{1,*}\)，如果不将 \(1\) 选入 \(T\) 则对应 \(0\) 状态，如果选入对应 \(2\) 状态，因此 \(f_{i,0}=f_{i,2}=1\)。

转移时先考虑 \(i\) 是否选入 \(T\)，然后转移时考虑合法性。那么考虑 \((i-1,i)\) 的交换情况。

• 如果关系不反转或反转都合法

  • \(i\) 不选入 \(T\)，对应 \(f_{i,0}\)，怎么搞都合法，得到 \(f_{i,0}\leftarrow f_{i-1,0}+f_{i-1,1}+f_{i-1,2}\)
  • \(i\) 选入 \(T\)，对应 \(f_{i,2}\)，同理 \(f_{i,2}\leftarrow f_{i-1,0}+f_{i-1,1}+f_{i-1,2}\)

• 如果关系必须不反转，即 \((0,0)\) 或是 \((1,1)\)

  • \(i\) 不选入 \(T\)，对应 \(f_{i,0}\)，此处只能不转，则 \((i-1)\) 也一定只能不转，\(f_{i,0}\leftarrow f_{i-1,0}+f_{i-1,2}\)

  • \(i\) 选入 \(T\)，\(f_{i-1,0/1/2}\) 都是一一对应转移过来，\(f_{i,x}\leftarrow f_{i-1,x}\)

    综上转移是

    \[f_{i,0}\leftarrow 2f_{i-1,0}+f_{i-1,2} \\ f_{i,1}\leftarrow f_{i-1,1}, f_{i,2}\leftarrow f_{i-1,2} \]

• 如果关系必须反转，即 \((0,1)\) 或是 \((1,0)\)

  • \(i\) 不选入 \(T\)，同理有 \(f_{i,0}\leftarrow f_{i-1,1}+f_{i-1,2}\)

  • \(i\) 选入 \(T\)，同理类似异或转移，不赘述

    综上转移是

    \[f_{i,0}\leftarrow 2f_{i-1,1}+f_{i-1,2} \\ f_{i,1}\leftarrow f_{i-1,0}, f_{i-1,2}\leftarrow f_{i-1,2} \]

做完了，最后答案就是 \(f_{n,0}+f_{n,1}+f_{n,2}\)。时间复杂度线性。

---

game

先考虑如果给定序列如何求，明显考虑贪心，升序排序后将所有数调整成 \(11\dots 1122\dots 2233\dots\) 的形式，要求操作次数最小。这个贪心有很多种刻画方法，考虑定义 \(b_i\) 表示在最优策略下 \(h_i\) 最后变成的数，则 \(b_i=\min(b_{i-1}+1,h_i)\)，则每个数贡献为 \(h_i-b_i\)。

考虑怎么优化，在增加一个数的时候快速维护。观察到，当 \(h_i\le b_{i-1}+1\) 时 \(b_i=h_i\)，这个数的贡献就是 \(0\)，我们称这些点是无用的，那么删掉无用的点是没有任何影响的，如图：

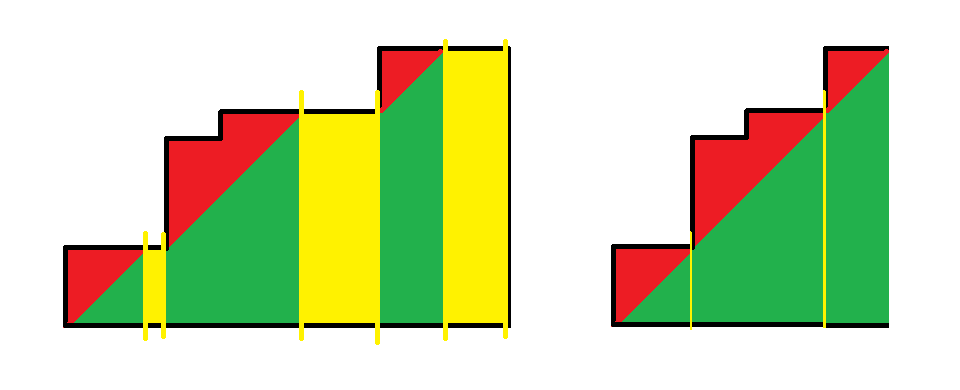
其相当于将黄色部分删去，这样红色部分的面积，即最终的答案，就可以用总和减去绿色等腰直角三角形的面积得到，记和为 \(S\)，有用的数的个数为 \(m\)，则答案可以表示为 \(S-\frac{m(m+1)}{2}\)。于是我们只需要动态维护有用的数以及其和即可。

考虑在值域上用线段树维护有用的数，加入一个数时，我们先钦定这个数是有用的，并先塞到线段树中。考虑一个数有用的条件，记 \(cnt_x\) 表示目前有用的数中 \(\le x\) 的数的个数和，则如果一种数 \(x\) 在加入后出现了 \(cnt_x>x\)，则说明数 \(x\) 需要被删掉一个，于是我们在线段树上找到最靠前的非法位置调整即可。于是做法就呼之欲出了，为了找到 \(cnt_x>x\)，变形得到 \(x-cnt_x<0\)，因此在值域线段树上对每个数维护 \(x-cnt_x\) 的最小值和最靠前位置，这个可以在 pushup 时简单做，然后如果加入这个数后非法了，我们取出最靠前的负位置并在其中删掉一个数，同时维护和即可，最后用提到的方法求出答案即可，时间复杂度是 \(O(n\log n)\)。

---

magician

对于二分图完美（完备）匹配，套路地考虑 Hall 定理，令 \(N(S)=\set{v\mid \exists u\in S,(u,v)\in E}\)，则存在完美匹配等价于 \(\forall S,|S|\le |N(S)|\)。使得所有的 \(S\) 都满足这个条件太难计数了，容斥一下，对存在 \(S\) 满足 \(|N(S)|>|S|\) 的图计数，考虑对每个这样的形式钦定 \(|N(S)|-|S|\) 最大的集合中 \(|S|\) 最小的作为代表元，可以证明，每个不合法的图其代表元都是唯一的，那么考虑对代表元容斥。

令 \(g_{S,T}\space (|S|>|T|)\) 表示考虑左部点集合为 \(S\)，\(N(S)=T\)，其不存在完美匹配且 \((S,T)\) 是代表元的方案数，\(G_{S,T}\) 表示这个导出子图的匹配方案数，即 \(N(S)=T\) 的方案数。那么考虑容斥掉代表元不是 \((S,T)\)，而是 \(S,T\) 的子集 \((S^{\prime},T^{\prime})\)，其需要满足 \(|S^{\prime}|-|T^{\prime}|\ge |S|-|T|\)，如图：

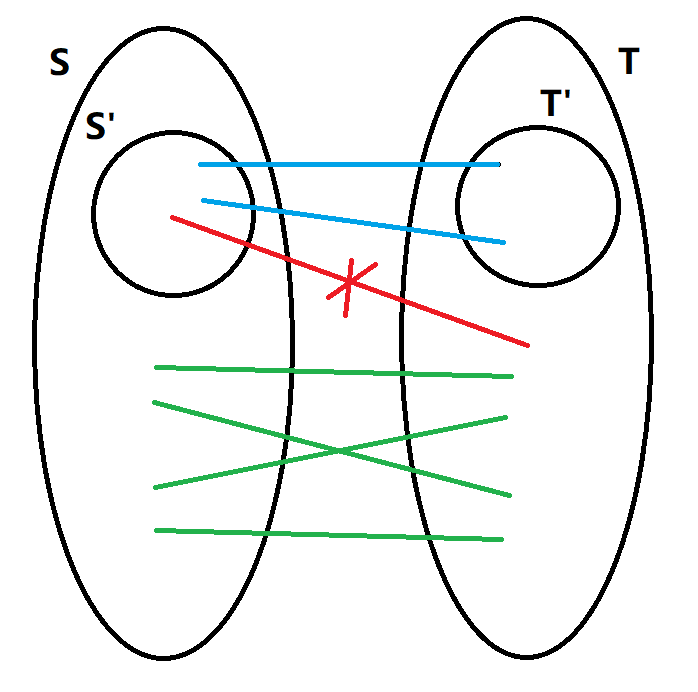
首先 \((S^{\prime},T^{\prime})\) 之间的方案数是 \(g_{S^{\prime},T^{\prime}}\)，并且要强制钦定 \(N(S^{\prime})=T^{\prime}\)，因此 \(S^{\prime}\to T\setminus T^{\prime}\) 之间不能有边，用 \(no_{S^{\prime},T\setminus T^{\prime}}\) 表示这个方案数。对于 \(S\setminus S^{\prime}\to T\setminus T^{\prime}\) 之间的连边，我们发现其一定要形成完美匹配，否则可以并上其中的某个不合法点集，这样 \(|N(S^{\prime})|-|S^{\prime}|\) 就变大了，不应在此处计数，因此我们还需要记 \(f_{S,T}\) 表示 \(S,T\) 之前有完美匹配的方案数，于是不难得到转移：

\[g_{S,T}=G_{S,T}-\sum_{S^{\prime}\subseteq S,T^{\prime}\subseteq T} [|S^{\prime}|-|T^{\prime}|\ge |S|-|T|]\times g_{S^{\prime},T^{\prime}}\times no_{S^{\prime},T\setminus T^{\prime}}\times f_{S\setminus S^{\prime},T\setminus T^{\prime}} \]

我们还需要求出 \(f_{S,T}\space (|S|\le |T|)\)，可以枚举子集 \((S^{\prime},T^{\prime})\) 表示其作为不合法位置且其作为代表元，即使用 \(g_{S^{\prime},T^{\prime}}\) 进行容斥：

\[f_{S,T}=G_{S,T}-\sum_{S^{\prime}\subseteq S,T^{\prime}\subseteq T} g_{S^{\prime},T^{\prime}}\times no_{S^{\prime},T\setminus T^{\prime}}\times f_{S\setminus S^{\prime},T\setminus T^{\prime}} \]

最终答案就是 \(f_{U,U}\)。时间复杂度可以分 \(S,T\) 计算量分别看，是 \(O(3^n\times 3^n)=O(9^n)\)。

---

graph

直接对 \(1\leadsto n\) 的最短路进行刻画似乎很难做，考虑最短路算法如dij，其会得到 \(d_i\) 表示 \(1\leadsto i\) 的最短路，那么我们可以暴搜出所有的 \([d_1=0,d_2,\dots,d_{n-1},d_n=k]\)，并求出满足的完全图数量即可。

加入一个点 \(u\) 时，假设枚举其 \(d_u=x\)，则对于所有 \((v,u)\)，需要满足 \(d_v+w\ge d_u\)，即 \(w\ge d_u-d_v\)，因此 \(w\in [d_u-d_v,L]\)，总共有 \(L-(d_u-d_v)+1\) 种选法。但是还需要存在 \(d_v+w=d_u\)，简单容斥掉所有 \(d_v+w>d_u\) 的情况即可得到连向点 \(u\) 的边的方案数。

但是直接暴力枚举是 \(O(L^n)\) 的，非常劣，不过注意到所有 \(d\ge k+1\) 的点贡献的方案都是相同的，因此可以将 \(\ge k+1\) 的看做一类，这样压到了 \(O(k^n)\)，还是无法通过，我们可以剪枝一下，从小到大确定每个 \(d_u=i\) 的点的位置，可以插板计算方案，这样可以做到 \(O\left(\binom{n+k}{n}\times (n+k)\right)\)的复杂度，可以通过。

---

ICPC-L

套路地考虑什么序列 \(p\) 能够被生成。显然我们可以考虑每个数 \(x\)，由于是推平操作，\(p_i=x\) 的位置一定构成一个区间，令原数组中 \(a_i\) 支配区间 \([l,r]\)，则最终 \(p\) 里 \(a_i\) 的出现位置 \([l^\prime,r^\prime]\subseteq [l,r]\)。于是问题可以转化成：

从前到后对于每个 \(a_i\)，可以选择 \(i\in [l^\prime,r^\prime]\in [l_i,r_i]\)，将 \([l^\prime,r^\prime]\) 全部覆盖成 \(a_i\)，求序列方案数。

考虑直接线性 \(\mathrm{dp}\)，令 \(f_i\) 表示 \(p\) 前 \(i\) 个数的方案数。对 \(a_i\) 而言，对于 \(j\in [l_i,r_i]\)，可以将某个 \([k,j]\) 全部盖成 \(a_i\)，因此有转移 \(f_j\leftarrow f_{k-1}\)，这个容易记录和优化掉，时间复杂度 \(O(n^2)\)。

---

painter

一个十字去覆盖实在是太难做了，考虑时光倒流，从后往前考虑染色情况。我们注意到最后一次操作，假设其在 \((x,y)\) 处操作了，则在 \((x,y)\) 处一定形成了一个完整的十字，将这个十字扣掉之后可以得到一个子矩阵。我们发现在新的子矩阵中行列变成了独立的，此时在新的子矩阵中我们可以任意选择行覆盖，也可以任意选择列覆盖。以行为例，不妨设我们要覆盖第 \(i\) 行，则我们可以先在 \((i,y)\) 染色，轮到 \((x,y)\) 染色时会直接抹除掉第 \(y\) 行的信息，因此等价于覆盖掉了第 \(i\) 行，列也同理。

那么问题变成将剩余的子矩阵染色的方案数，令 \(f_{i,j}\) 表示 \(i\times j\) 的子矩阵能够被染色到的状态方案数。

对于行而言，我们枚举 \(k\) 表示钦定恰好有 \(k\) 行被染成同色的一行，乘上容斥系数 \((-1)^{k-1}\)，得到转移：

\[f_{i,j}\leftarrow (-1)^{k-1}\binom{i}{k}C^k\cdot f_{i-k,j} \]

列同理，可以得到：

\[f_{i,j}\leftarrow (-1)^{k-1} \binom{j}{k}C^k\cdot f_{i,j-k} \]

但是不难发现这样会算重，对于一个十字，其会被先染行再染列和先染列再染行重复计数，因此我们需要减掉形成十字的情况，枚举 \(x,y\) 表示有 \(x\) 行和 \(y\) 列构成了同色的十字，分析得容斥系数为 \((-1)^{x+y}\times (-1)=(-1)^{x+y+1}\)，有转移：

\[f_{i,j}\leftarrow (-1)^{x+y+1}\binom{i}{x}\binom{j}{y}C\cdot f_{i-x,j-y} \]

最终答案就是 \(Cnm\cdot f_{n-1,m-1}\) 吗？并非，这样还是会记重，因为如果最终矩阵中和最后一次操作同颜色的位置构成了多个十字，那么枚举每个十字会计算重复。因此可以类比 \(\mathrm{dp}\) 时的做法进行容斥，枚举 \(x,y\) 表示最终矩阵中和最后一次操作同颜色的位置构成了 \(x\) 行、\(y\) 列交错，则

\[ans=\sum_{x=1}^n\sum_{y=1}^m(-1)^{x+y}\binom{n}{x}\binom{m}{y}C\cdot f_{n-x,m-y} \]

直接计算是 \(O(n^4)\) 的，不难用脚优化到 \(O(n^3)\)。

---

dune

操作会作用到当前的最大值上，设当前最大值 \(x\) 的位置位于 \(p_1,p_2,\dots p_k\) 这些位置，则操作会从两边往内修改。令 \(mxl_i,mxr_i\) 分别表示 \(p_i\) 左侧比 \(x\) 小的最大数和右侧比 \(x\) 小的最大数。那么修改后 \(a_{p_i}\) 能够取到的值的下界显然就是 \(\min(mxl_i,mxr_i)\)，并且这个下界是可以被达到的，满足 \(mxl_i\le mxr_i\) 的是一段前缀，其余部分是一个后缀，因此可以在这个前缀中从左边扫，后缀中从右往左扫。

考虑这样一个过程，我们从大往小在值域上枚举 \(x\)，并考察有哪些已经枚举过的位置会变成这个数。不妨设 \(x\) 出现的左右端点是 \(l,r\)，分类讨论一下，对于 \(i\in (l,r)\)，这些位置无论是往左扫还是往右扫都会变成 \(x\)，因此我们直接将这些数变成 \(x\) 并更新操作次数。而对于 \(i<l\)，如果其往右扫则会变成 \(x\)，我们自然希望这些数取到更小的数，即我们希望其从左边扫，同理对于 \(i>r\)，我们希望其从右边扫。可以看做每个位置都有从左扫/从右扫/不确定方向的状态，不妨用 ?,←,→ 分别表示这些状态，手玩样例模拟这个过程：

1 4 2 4 0 2
. ? . ? . .
x=4, l=2, r=4

1 4 2 2 0 2
. ← ? ? . ?
x=2, l=3, r=6

1 1 2 2 0 2
? ? → → . →
x=1, l=1, r=2

0 0 0 0 0 0
x=0, l=1, r=6

这个过程其实可以简单维护，注意到每次操作后一定是 ←←←???→→→ 的形态，因此我们只需要维护?所处的区间以及在树状数组上维护?的位置即可，时间复杂度为 \(O(n\log n)\)。

具体的，设目前?所处的区间为 \([L,R]\)，且数 \(x\) 的出现区间在 \([l,r]\)，分类讨论：

• 若 \(r<L\)，即形成 \([l,r]\dots [L,R]\)

  那么 \(x\) 出现的位置要被标为?，原先 \([L,R]\) 中的?都被变成了←，而 \((r,L)\) 中的←会使这些位置作用在当前数上，因此这些位置会变成 \(x\)，然后标记重新置为?，因此?的区间应为 \([l,L)\)

• 若 \(l>R\)，即形成 \([L,R]\dots[l,r]\)

  同理，\((R,l)\) 中的→会作用到当前的 \(x\)，因此这些位置变成 \(x\)，标记变成?，因此新区间为 \((R,r)\)。

• other

  没有其他位置变成?，区间为 \([l,r]\)。

然后遍历位置，在树状数组上更新?即可。

---

graph

每个有前驱的节点一定不会自发点亮不好处理，因此我们考虑那些没有前驱的节点，即 \(\texttt{DAG}\) 上入度为 \(0\) 的那些叶子，这些叶子可以自由地选择发光或是不发光，若某个叶子发光，则其会将可达的所有点都点亮，记这个点集为 \(S_u\)，则可以将这个限制描述成 \(u\) 发光则 \(S_u\) 中的所有点都发光。假设现在我们知道点 \(x\) 是发光的，可以发现这等价于可达 \(u\) 的叶子中存在一个发光的点，那么可以任意选择叶子集发光，假设这些叶子编号为 \(p_1,p_2,\dots ,p_k\)，则不难发现一定能发光的点集就是 \(\displaystyle\bigcap_{i=1}^k S_{p_i}\)。于是正解就呼之欲出了，先用 \(\texttt{DAG}\) 可达性统计得到叶子的 \(S_u\)，根据经典追忆此处用 bitset 即可。然后我们需要对每个点处理出反图中可以到达的叶子的 \(S\) 交集状物，可以在反图中再跑一次拓扑即可。对于询问，每次给出的点之间是独立的，因此答案就是每个单点的答案并起来。

时间复杂度 \(O\left(\frac{nm+qn^2}{\omega}\right)\)，可以通过。

---

chess

考虑如何实现染色，对于每种颜色，其在原图中对应了一个环：

模拟转圈的过程，颜色不断交替，直接即可

参考

---

cake

首先我们知道答案的上界是 \(d\)，因为可以用 \(d\) 刀切无限小的 \(d\) 块。

那么答案在什么情况下才可以缩小呢，先假设我们要切出的蛋糕大小为 \(x\)，则我们发现唯一能缩小的方法就是在 \(\frac{a_i}{x}=t\) 为整数时，我们可以只切 \(t-1\) 刀就能切出 \(t\) 块，这种情况下恰好省下了 \(1\) 刀。

那么如果我们想让答案变小，则我们发现切的蛋糕大小一定在下面这些集合中：

\[\left\{\frac{a_1}{1},\frac{a_1}{2},\frac{a_1}{3},\dots,\frac{a_1}{d}\right\}\left\{\frac{a_2}{1},\frac{a_2}{2},\frac{a_2}{3},\dots,\frac{a_2}{d}\right\}\dots\left\{\frac{a_n}{1},\frac{a_n}{2},\frac{a_n}{3},\dots,\frac{a_n}{d}\right\} \]

总共有 \(n\times d\) 个方案，对于一个固定的 \(x\)，我们可以先判断其是否可以切出 \(\ge d\) 个块，如果可以，我们再看看这个 \(x\) 可以贡献多少个整除时的 \(-1\)，每个可以被整除的决策，记其切除块数为 \(w_i\)，其意义是，得到 \(w_i\) 块，需要 \(w_i-1\) 次切。根据贪心，我们肯定是按照 \(w_i\) 从小到大处理，这样可以贡献尽量多的 \(-1\)。这样非常暴力的做其时间复杂度是 \(O(n^2d\log n)\) 的，无法通过，需要进行优化。

对于判断 \(x\) 是否可以切出 \(\ge d\) 个块，注意到这个可行性是有单调性的，考虑先将所有的分数约分后都存起来，从小到大排序后离散化，这样就可以二分找到最大的 \(L\) 使得其可以切出 \(\ge d\) 个块，现在考虑对于 \(\le L\) 的分数 \(x\) 求出答案。对于化简后和 \(x\) 相等的分数，将其按照 \(w_i\) 从小到大排序后做上述的贪心即可。时间复杂度为 \(O(nd\log nd)\)，可以通过。