CF Round 1045 (Div. 2) 比赛总结

Codeforces Round 1045 (Div. 2)

A. Painting With Two Colors

反应力还是不够快，注意到能够覆盖一定是和 \(n\) 同奇偶，那么 \(b\not\equiv n\pmod 2\) 的可以直接 \(\mathrm{pass}\)，而 \(a\not\equiv n\pmod 2\) 并且 \(a>b\) 的话 \(b\) 没办法盖住非法的 \(a\)，也是直接 \(\mathrm{pass}\)，剩余情况就是合法的。

B. Add 0 or K

其实就是要构造 \(0\le b_i\le k\)，使得 \(\gcd(a_1+b_1k,\dots,a_n+b_nk)>1\)。赛时并没有一眼，先去做 \(\texttt{C}\) 了。

考虑 \(\gcd=g\)，则 \(\forall i,(a_i+b_ik)\bmod g=0\)，即 \([(a_i\bmod g)+(b_i\bmod g)(k\bmod g)]\bmod g=0\)，这个 \((k\bmod g)\) 很难处理，手玩样例想到取 \(g=k-1\)，这样对于 \(k>2\)，有 \(k\bmod g=k\bmod (k-1)=1\)，原式就变成 \((a_i\bmod g+b_i\bmod g)\bmod g=0\)，直接构造出 \(b_i\equiv -a_i\pmod g\) 即可，满足要求。

需要特殊处理 \(k\le 2\)。若 \(k=1\)，相当于 \(+0/1\)，全部构造成偶数即可。若 \(k=2\)，能构造出 \(+0/2/4\)，手玩样例猜测 \(\gcd=3\)，并且在模 \(3\) 意义下相当于 \(+0/2/1\)，分模 \(3\) 余数讨论即可。

官解： 取 \((k-1)\) 会导致分类讨论，考虑取 \(g=k+1\)，并巧妙的取 \(b_i=a_i\bmod (k+1)\)，于是 \(a_i+b_ik=b_i+b_ik=b_i(k+1)\equiv 0 \pmod {k+1}\)，并且 \(0\le b_i\le k\)，完成构造。

C. Even Larger

很 \(\texttt{Trivial}\) 的问题，每个 \(odd-even-odd\) 的限制最强，那么直接从前往后扫，把后面的贡献完了就贡献前面的即可。

D. Sliding Tree

没有场切，有一定思维难度。

考虑这棵树的直径，我们发现一次 \(\texttt{Slide}\) 操作最多使得直径长度 \(+1\)，因为操作相当于将一棵子树移动一个单位，直径长度最多变化 \(1\)。而最终的目标是一条链，直径长度为 \((n-1)\) 与之等价，因此相当于要用操作使得直径增长到 \((n-1)\)，最优显然是每次操作都能使直径长度 \(+1\)，假设原树直径长度为 \(l\)，那么操作次数下界为 \((n-1-l)\)，下面我们将构造操作方法使其能取到这个下界，即每次都使直径长度 \(+1\)。

随便取直径一端定根。取直径上从上到下的一条边 \((u,v)\)，并且 \(v\) 有不在直径上的一个儿子 \(w\)，考虑这三个点依次作为 \((a,b,c)\) 会有什么效果：

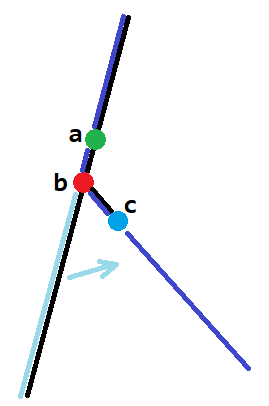
此时 \(v\) 下端的一段直径就会被接到 \(w\) 处，直径多出了 \((v,w)\) 一条边，完成了直径长度 \(+1\) 的构造。因此我们只需要找到直径，取满足要求的 \((u,v,w)\) 即可，时间复杂度 \(O(n)\)。

E. Power Boxes

有趣交互，建议和 \(\texttt{D}\) 进行一个 \(\textbf{swap}\)

一个比较直接的想法就是对每个位置都 \(\mathrm{throw}\) 一下，记第 \(i\) 个位置的结果是 \(d_i\)，那么我们或许可以通过 \(d_{i+1},d_{i+2}\) 来确定 \(a_i\)。若 \(d_{i+1}\ne d_{i+2}\) 那么可以直接判断，若 \(d_{i+1}=d_i+1\) 就有 \(a_i=1\)，否则 \(a_i=2\)。但是如果 \(d_{i+1}=d_{i+2}\)，就不能直接确定了，考虑怎样使用这个 \(\mathrm{swap}(a_i,a_{i+1})\) 的操作。

注意到，\(a\) 中相邻两个值至多只有一个不确定。证明：如果 \(i\) 不确定，那么 \(d_i=d_{i+1}+1\)，故 \(d_i\ne d_{i+1}\)，而对 \((i-1)\) 来说这就表示 \(d_{i^{\prime}+1}\ne d_{i^{\prime}+2}\)，故 \((i-1)\) 一定是被确定的。

所以如果 \(a_i\) 不确定，我们可以执行一次 \(\mathrm{swap}(a_i,a_{i+1})\)，此时 \(a_{i+1}\) 一定是可以被确定的，即保证了 \(a_{i+2}\ne a_{i+3}\)，换过来之后，再跑一遍 \(\mathrm{throw}(i+1)\)，由于相对 \((i+1)\) 来说的后面两个 \(d\) 都已经确定，所以 \(a^{\prime}_{i+1}\) 即 \(a_i\) 就可以被确定。

分析一下操作次数，假设有 \(x\) 个位置可以直接确定，则有 \((n-x)\) 个无法确定，操作次数就是 \(x+2(n-x)=2n-x\)，由于相邻两个数至少有一个被确定，所以 \(x\ge \left\lceil\frac{n}{2}\right\rceil\)，因此总操作次数不会超过 \(\frac{3n}{2}\)，满足要求。