算法第二章作业-实验报告

实践报告任选一题进行分析。内容包括：

1. 1. 实践题目名称： 　　7-1 最大子列和问题
   2. 　　问题描述:

 

给定K个整数组成的序列{ N​1​​, N​2​​, ..., N​K​​ }，“连续子列”被定义为{ N​i​​, N​i+1​​, ..., N​j​​ }，其中 1。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 }，其连续子列{ 11, -4, 13 }有最大的和20。现要求你编写程序，计算给定整数序列的最大子列和。

 

本题旨在测试各种不同的算法在各种数据情况下的表现。各组测试数据特点如下：

 

1. 数据1：与样例等价，测试基本正确性；
2. 数据2：102个随机整数；
3. 数据3：103个随机整数；
4. 数据4：104个随机整数；
5. 数据5：105个随机整数；

 

输入格式:

 

输入第1行给出正整数K (≤)；第2行给出K个整数，其间以空格分隔。

 

输出格式:

 

在一行中输出最大子列和。如果序列中所有整数皆为负数，则输出0。

---

 

1. 算法描述

　　　　利用分治法。将区间以中间为基准一分为二，将最大子列和问题划分为左区间、右区间、横跨左右区间的最大子列和问题。其中左右区间可以通过递归完成，中间的最大子列和要另外处理。

递归：函数+判断语句；  基例+链条

 

 

 　　

---

 

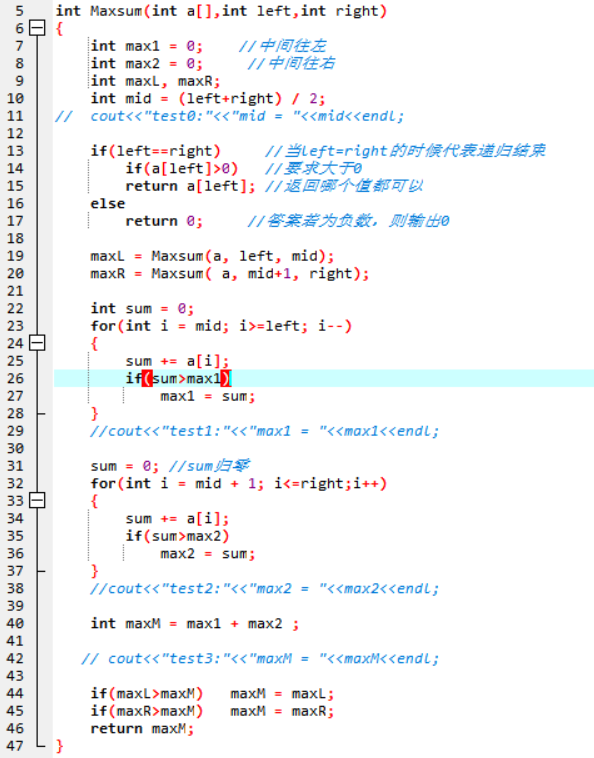
3.算法时间及空间复杂度分析（要有分析过程）

　　　　时间复杂度：

    将n划分成{n/k，n/k,...,n/k}  k个问题。

　　　　　　T(n) = { O(1)   , n<=c

　　　　　　　　　 {2T(n/2) + O(n)  ,n>c

　　　　　　解得T(n) = O（nlogn) 

　　　　　　 空间复杂度： O(n) 用于存储输入数据。

1. 心得体会（对本次实践收获及疑惑进行总结）

　　

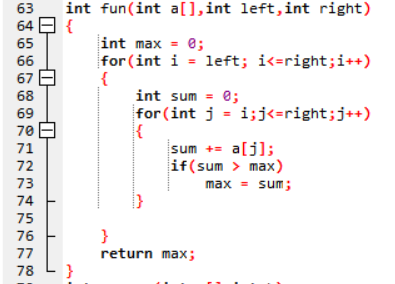
 　　　　一开始对分治法理解不够，递归的思想没加入到分治法里面。

　　　　仅仅是将原问题一分为二，而不是递归的一分为二。

　　　　于是就写出了如上的fun函数，求解左半边的max和右半边的max。

　　　　What  a joke.

　　　　后来删掉fun，将原来的maxnum函数改成递归函数，问题迎刃而解。

　　　　这就是分治法吗？i了i了。

　　　　运用和掌握一个算法的过程有些曲折，用题目来巩固这种算法思想，体验很好。