炼石#8t2

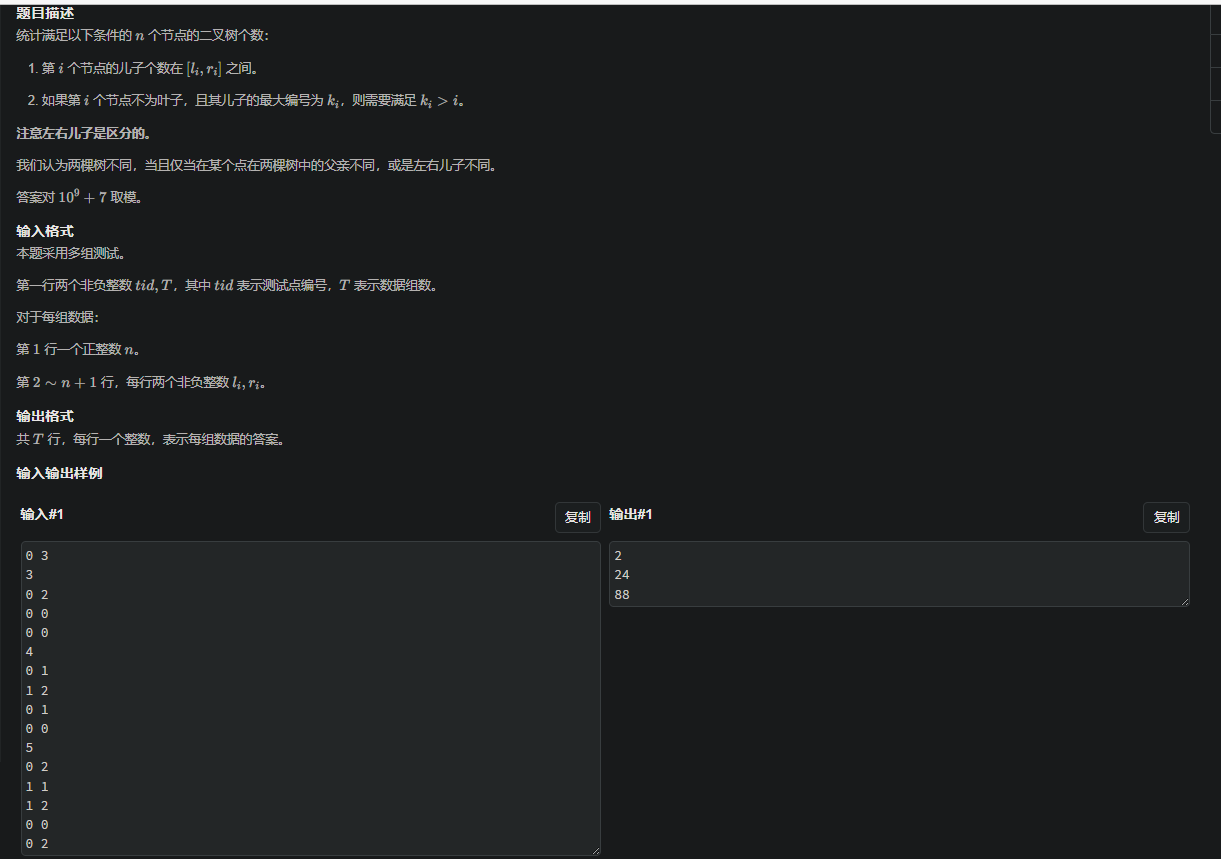
赛时调了很长时间， 应该到蓝了， 但是比较暴力了
组合数学 dp[i][j][k]代表选到第i个点，j棵树然后需求k个儿子
我们注意到可以分类讨论，分为三种情况
{
没有儿子
一个儿子
两个儿子
}
其中第一种情况可以{
首先考虑自己成为一个树转移显然：：dp[i][j + 1][k] = (dp[i][j + 1][k] + dp[i - 1][j][k]) % mod;
另一情况为做别人的儿子显然 ：：if(k > 0) dp[i][j][k - 1] = (dp[i][j][k - 1] + dp[i - 1][j][k] * k) % mod;
}
第二种情况可以{
首先自己成为一颗树dp[i][j + 1][k + 1] = (dp[i][j + 1][k + 1] + 2 * dp[i - 1][j][k]) % mod;//因为要钦定自己是要左儿子还是右儿子所以*2
其次考虑接一个上去 dp[i][j][k] = (dp[i][j][k] + 2 * dp[i - 1][j][k] * k) % mod;
}
第三种情况 {
略（同理
dp[i][j + 1][k + 2] = (dp[i][j + 1][k + 2] + dp[i - 1][j][k]) % mod;//dandu
dp[i][j][k + 1] = (dp[i][j][k + 1] + (dp[i - 1][j][k] * k % mod) + (2 * dp[i - 1][j][k] * j % mod)) % mod;
if(j > 1) dp[i][j - 1][k] = (dp[i][j - 1][k] + 2 * dp[i - 1][j][k] * k * (j - 1)) % mod;
}

#include <bits/stdc++.h>
#define MAXN 310
#define mod 1000000007
#define int long long
using namespace std;
namespace SHuxinn{
	int n,l[MAXN],r[MAXN] , dp[MAXN][MAXN][MAXN * 2];
    void Sx5(){
    	int tid , _;
    	cin >> tid >> _;
        while(_--){
			memset(dp, 0, sizeof(dp));
        	dp[0][0][0] = 1;
            cin >> n;
            for(int i = 1 ; i <= n ; i++)
                cin >> l[i] >> r[i];
            for(int i = 1 ; i <= n ; i++){
                for(int j = 0 ; j < i ; j++){
                    for(int k = 0 ; k <= n * 2 ; k++){
                        if(!dp[i - 1][j][k]) continue;
                        if(l[i] == 0){//0geerzi
                            dp[i][j + 1][k] = (dp[i][j + 1][k] + dp[i - 1][j][k]) % mod;//dandu
                            if(k > 0) dp[i][j][k - 1] = (dp[i][j][k - 1] + dp[i - 1][j][k] * k) % mod;
                        }
                        if(l[i] < 2 && r[i] >= 1){//1geerzi
                            dp[i][j + 1][k + 1] = (dp[i][j + 1][k + 1] + 2 * dp[i - 1][j][k]) % mod;//dandu
                            dp[i][j][k] = (dp[i][j][k] + 2 * dp[i - 1][j][k] * k) % mod;
                        }
                        if(r[i] == 2){//lianggeerzi
                            dp[i][j + 1][k + 2] = (dp[i][j + 1][k + 2] + dp[i - 1][j][k]) % mod;//dandu
                            dp[i][j][k + 1] = (dp[i][j][k + 1] + (dp[i - 1][j][k] * k % mod) + (2 * dp[i - 1][j][k] * j % mod)) % mod;
                            if(j > 1) dp[i][j - 1][k] = (dp[i][j - 1][k] + 2 * dp[i - 1][j][k] * k * (j - 1)) % mod;
                        }
                    }
                }
            }
            
            cout << dp[n][1][0] << endl;
        }
        
        return;
    }
}
signed main(){
	freopen("tree.in","r",stdin);
    freopen("tree.out","w",stdout); 
    SHuxinn::Sx5();
	return 0;
}