炼石#8 T1

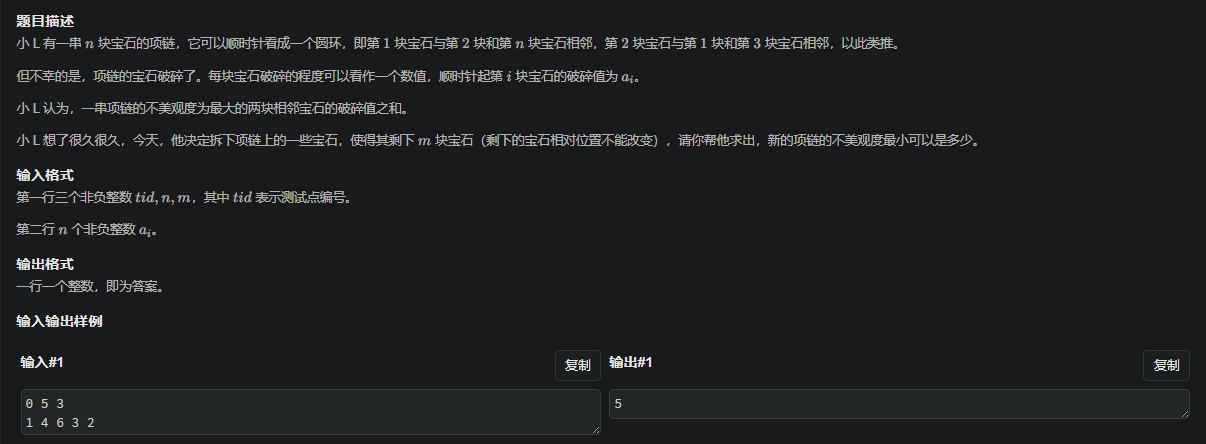
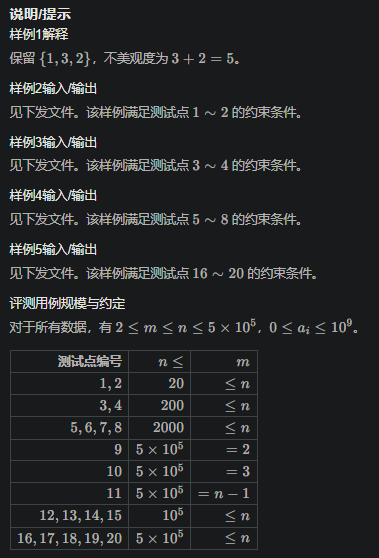
赛时很快想出切掉，感觉比t2恶心🤢，可能是二分做法的问题（bushi
想法简单，贪心想法保留m个最小的 ，于是二分k用来区分大数和小数 ， 如果小于k/2为小数 ， 显然小数是必拿 ，然后在每个小数之间最多只能有一个大数，且需要满足小数加这个大数小于k即可
然后如果最后长度小于m就找大，大于等于m就找小细节看注释

#include <bits/stdc++.h>  // 包含所有标准库头文件，方便快速编写代码
#define MAXN 500010       // 定义宝石数量的最大上限
#define inf 2000000000    // 定义二分查找的右边界（足够大的数）
#define int long long     // 将int类型重定义为long long，避免整数溢出
using namespace std;

namespace SHuxinn {
    int n, m, a[MAXN];  // n：原项链的宝石总数；m：需要保留的宝石数；a[]：存储每块宝石的破碎值
    vector<int> s;      // 存储满足「a[i] ≤ 当前二分的k/2」的宝石位置（用于辅助判断相邻和）

    // 检查：当最大允许的相邻宝石破碎值之和为k时，能保留的宝石数量是否 ≥ m
    int check(int k) {
        s.clear();  // 每次检查前清空容器
        for (int i = 1; i <= n; i++) {
            // 筛选出「自身破碎值 ≤ k/2」的宝石（这类宝石更容易与其他宝石相加不超过k）
            if (a[i] <= k / 2) {
                s.push_back(i);
            }
        }

        if (s.empty()) {  // 若没有宝石满足「a[i] ≤ k/2」，则任意两块相加都＞k，最多只能留1块
            return 0;
        }

        if (s.size() == 1) {  // 只有1块满足「a[i] ≤ k/2」的宝石，检查是否能找到另一块与之相加≤k
            int l = s[0];
            for (int i = 1; i <= n; i++) {
                if (i != l && a[i] + a[l] <= k) {  // 找到不同的宝石且和≤k
                    return 2;  // 能保留2块
                }
            }
            return 1;  // 找不到，只能保留1块
        }

        int last = 0;   // 记录上一个「a[i] ≤ k/2」的宝石位置
        int ans = 0;    // 记录在「a[i] ≤ k/2」的宝石之间，额外能保留的宝石数量
        int r = s.size() - 1;  // 环形结构中，最后一个「a[i] ≤ k/2」的宝石在s中的索引

        for (auto l : s) {  // 遍历所有「a[i] ≤ k/2」的宝石位置
            if (last == 0) {  // 处理第一个「a[i] ≤ k/2」的宝石（环形的“开头”情况）
                // 取「当前宝石」和「最后一个满足条件的宝石」的较大值（因为是环形，首尾相邻）
                int maxx = max(a[l], a[s[r]]);
                bool vis = 1;  // 标记是否在“首尾之间”找到可保留的宝石

                // 检查「第一个满足条件的宝石」左边的宝石（环形的左半部分）
                for (int j = 1; j < l && vis; j++) {
                    if (maxx + a[j] <= k) {  // 找到能与maxx相加≤k的宝石
                        ans++;  // 保留这块宝石
                        vis = 0;  // 标记已找到，退出循环
                    }
                }

                // 检查「最后一个满足条件的宝石」右边的宝石（环形的右半部分）
                for (int j = s[r] + 1; j <= n && vis; j++) {
                    if (maxx + a[j] <= k) {  // 找到能与maxx相加≤k的宝石
                        ans++;  // 保留这块宝石
                        vis = 0;  // 标记已找到，退出循环
                    }
                }

                last = l;  // 更新上一个满足条件的宝石位置为当前l
                continue;
            }

            // 处理非第一个「a[i] ≤ k/2」的宝石（检查当前l与上一个last之间的宝石）
            int maxx = max(a[last], a[l]);  // 上一个和当前满足条件的宝石的较大值
            for (int i = last + 1; i < l; i++) {
                if (maxx + a[i] <= k) {  // 找到中间能保留的宝石
                    ans++;  // 保留这块宝石
                    break;  // 只要找到一个就停止（尽可能多保留，找到即满足）
                }
            }

            last = l;  // 更新上一个满足条件的宝石位置
        }

        // 总保留数 = 满足「a[i] ≤ k/2」的宝石数 + 中间额外保留的宝石数
        return s.size() + ans;
    }

    void Sx5() {
        int tid;
        cin >> tid >> n >> m;  // 输入：测试点编号、原宝石数n、需要保留的宝石数m

        int maxx = 0;
        for (int i = 1; i <= n; i++) {
            cin >> a[i];        // 输入每块宝石的破碎值
            maxx = max(maxx, a[i]);  // 记录最大的破碎值（二分初始参考）
        }

        // 二分查找：最小的「最大相邻和」
        int l = 0, r = inf, ans;  // l：左边界；r：右边界；ans：最终答案
        while (l <= r) {
            int mid = (l + r) / 2;  // 当前猜测的「最大相邻和」
            if (check(mid) >= m) {  // 若能保留至少m块宝石
                r = mid - 1;        // 尝试更小的「最大相邻和」
                ans = mid;          // 记录当前可行的答案
            } else {
                l = mid + 1;        // 否则需要更大的「最大相邻和」
            }
        }

        cout << ans << endl;  // 输出最小的「不美观度」（即最小的最大相邻和）
    }
}

signed main() {
    freopen("necklace.in", "r", stdin);   // 重定向输入到文件necklace.in
    freopen("necklace.out", "w", stdout); // 重定向输出到文件necklace.out
    SHuxinn::Sx5();  // 调用命名空间内的核心逻辑函数
    return 0;
}

ps::注释是ai写的只粗略的看了一眼，有问题欢迎纠正