ODE 笔记
速成版速成笔记,请结合李思讲义食用!
深度好友链:https://1592063346.github.io/learn/ode
- Ch1 Introduction
- Ch2 Linear Equations
- Ch3 Nonlinear Equations
- Ch4 Power Series Solutions
- Ch5 Boundary Value Problem
- Ch6 Calculus of Variations 变分法
Ch1 Introduction
1.1 Differential Equations and Basic Concepts
Def
- linear, nonlinear
- order
- homogeneous, have constant coefficients
Theorem (ODE 的等价形式)
- All ODEs can be equivalently described by a system of 1st-order ODE.
![image]()
\(\Leftrightarrow\)![image]()
![image]()
\(\Leftrightarrow\)![image]()
![image]()
![image]()
Tool
- direction field (\(\frac{dy}{dt}=f(t,y)\), draw \((1,f)\) at \((t,y)\))
- integral curve (tangent to \((1,f)\))
1.2 Examples of Solving Tricks
Integrating Factor
![image]()
\(\Rightarrow\)![image]()
A Necessary Condition
- For
![image]()
We need![image]()
- If this doesn't work, try multiply an integrating factor:
![image]()
We need![image]()
Seperation of Variables
- For \(\frac{dy}{dt}=\varphi(t,y)=f(y)g(t)\)
\(\Rightarrow \frac{dy}{f(y)}=g(t)dt\)
Change of Variable
Linear Change
![image]()
We let![image]()
Homogeneous Equation 齐次方程
-
\[\frac{dy}{dt}=f(\frac{y}{t}) \]We let $$u(t)=\frac{y(t)}{t}$$\[\Rightarrow \frac{du}{dt} = -\frac{y}{t^2}+\frac{1}{t}\frac{dy}{dt} \]\[\Rightarrow \frac{du}{dt} = \frac{f(u)-u}{t} \]
Ch2 Linear Equations
2.1 Linear System with Constant Coefficients 常系数线性系统
1st Order Homogeneous System 一阶齐次系统
Theorem(一阶齐次系统通解)
- 对 \(\forall\) 列向量 \(\vec y_0\in \R^n\),方程 \(\frac{d}{dt}\vec y=A\vec y\) 有唯一解满足初始条件 \(\vec y(0)=\vec y_0\),这个解可以显式地表示为 \(\vec y(t)=e^{tA}\vec y_0\).
Exponential Matrix 指数矩阵
- 略,见 pp. 15 - 18
1st Order Inhomogeneous System 一阶非齐次系统
其中 \(A\) 是 \(n\) 阶常矩阵,\(\vec b(t)\) 是与 \(t\) 有关的 \(n\) 维列向量。
Theorem(一阶非齐次系统通解)
- 对 \(\forall\) 列向量 \(\vec y_0\in \R^n\),方程 \(\frac{d}{dt}\vec y=A\vec y+\vec b(t)\) 有唯一解满足初始条件 \(\vec y(0)=\vec y_0\),这个解可以显式地表示为 \(\vec y(t)=e^{tA}\vec y_0 + \int_0^t e^{(t-s)A}\vec b(s)ds\).
n-th order homogeneous equation n 阶齐次方程
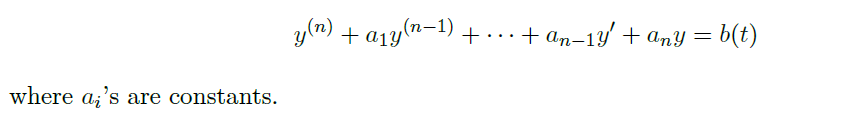
且 \(\vec b(t)=0\)
Def
- the characteristic polynomial of the equation 方程的特征多项式
![image]()
\(\Leftrightarrow\)![image]()
\(\Rightarrow\)![image]()
Proposition(n 阶齐次方程通解)
![image]() 是方程
是方程 ![image]() 的 n 个线性独立的解。
的 n 个线性独立的解。- 通解可以由以上解的线性组合给出。特别地,当存在复根 \(\alpha +i\beta\) 时,有解
![image]()
可以用实方程表示:![image]()
![image]()
- 为了确定唯一解,我们需要 n 个初始条件
![image]()
来确定线性组合的系数。
一般解法:解特征方程确定线性独立解,解初始值方程确定系数。
n-th order inhomogeneous equation n 阶非齐次方程
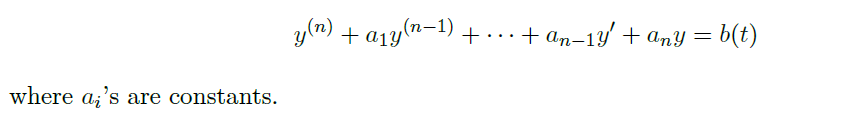
- 观察到:通解 = 特解 + 齐次方程通解,其中齐次方程为
![image]()
- 我们只要找一个特解。可以把方程写成一阶非齐次形式
![image]()
由之前的讨论,可以知道有一个特解是![image]()
带矩阵的积分可能很复杂,之后会有一种方法:variation of parameters。目前,可以通过猜测确定特解。
2.2 Long-term Behavior
在这节中,我们考虑当 t 变大时,方程 \(\frac{d\vec y}{dt}=A\vec y\) 的解的行为,即 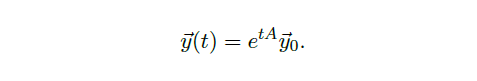
的行为。先讨论如何计算 \(e^{tA}\)。
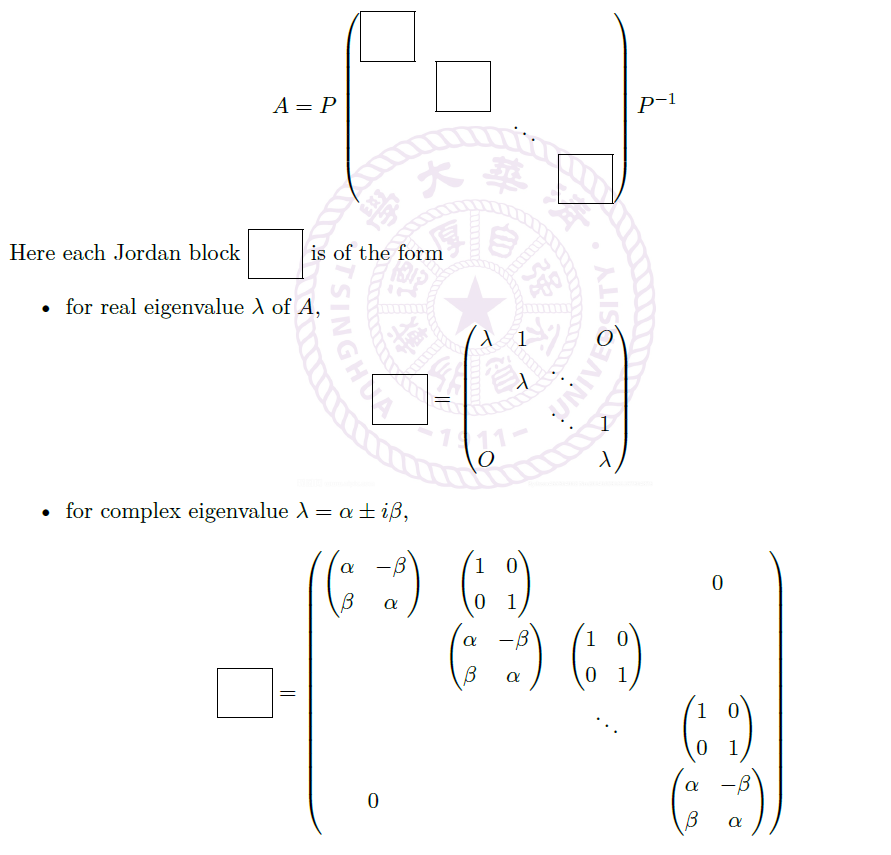
Jordan Canonical Form
复 Jordan 标准型
- 任给方阵 \(A\),我们可以写成
![image]()
![image]()
其中,\(N\) 幂零,\(D\) 和 \(N\) 交换。 - 考虑 \(e^{tA}\)。有:
![image]()
由于 \(D\) 是对角阵,有![image]()
由于 \(N\) 幂零,有![image]()
Proposition(参数矩阵的所有特征值实部为负时,方程的解在 t 很大时趋向 0)
实 Jordan 标准型
- 矩阵 \(A\) 可以写成
![image]()
Two-dim System 二维系统
略,见 pp. 30 - 33
2.3 Nonautonomous Linear Equations 非自治线性方程
这节我们讨论 
其中 \(A(t)\) 不再是常矩阵。
Homogeneous Case 齐次非自治线性方程
- 先考虑齐次情况,方程为
![image]()
Def
- path-ordered exponential:
![image]()
Proposition(path-ordered exponential 的性质)
解决 Homogeneous Case
General Case - Variation of Parameters
这节我们讨论 
观察到:通解 = 特解 + 齐次方程通解,其中齐次方程通解由 path-ordered exponential 给出,下面介绍一种方法给出特解。
-
设已经找到齐次方程的 n 个线性独立的解
![image]()
我们希望找到一个特解 \(y(t)\),它的形式是![image]()
可以用 Cramer's rule 解决:![image]()
因此,特解为![image]()
-
称以上的 \(W(t)\) 为 Wronskian determinant(Wronskian 行列式)
Ch3 Nonlinear Equations
3.1 Local Solutions 局部解的存在性和唯一性
经过有限时间 t,非线性系统的解很可能会爆炸,即使系统的系数非常好。然而,对很多非线性系统,给定初始条件,局部解是可以找到的。
在这一小节中,我们通过引入算子 \(T\) ,并利用压缩映射的性质,来完成局部解的存在性和唯一性的证明。
Def
- operator \(T\):
对于非线性方程![image]()
记 operator \(T\) 为![image]()
我们有![image]()
即 \(y\) 是 \(T\) 的不动点. - contraction mapping 压缩映射:
![image]()
- fixed point 不动点
Theorem(The Contraction Mapping Theorem 压缩映射不动点存在且唯一)
Def
- Lipschitz condition:
![image]()
- 典例:\(U\) 是凸集,\(\vec F(\vec y,t)\) 关于 \(\vec y\) 是 \(C^1\) 的,且 \(|\partial_{y^i}\vec F|≤M\),则 \(\vec F(\vec y,t)\) 满足 Lipschitz 条件,且 \(L=M\)
Theorem(算子 \(T\) 在局部是压缩映射)
- 在初始值问题
![image]() 中,假设 \(\vec F\) 在 \(U\subset \R^n×\R\) 中关于 \(y\) 满足 Lipschitz 条件,其中 \((\vec \xi,t_0)\in U\)。记
中,假设 \(\vec F\) 在 \(U\subset \R^n×\R\) 中关于 \(y\) 满足 Lipschitz 条件,其中 \((\vec \xi,t_0)\in U\)。记 ![image]()
则存在足够小的 \(\varepsilon, \delta\),使得 \(T\) 在 \(X_{\varepsilon, \delta}\) 上是压缩映射。 - 证明思路:
- 首先,可以找到足够小的 \(\varepsilon, \delta\),使得
![image]()
观察到,![image]() 是一个以常函数 \(x(t)=\vec \xi\) 为中心的闭球。
是一个以常函数 \(x(t)=\vec \xi\) 为中心的闭球。 - 由 \(\vec F\) 的连续性,可以设
![image]()
由 \(T\) 的表达式,有![image]()
缩小 \(\varepsilon\) 使得 \(K\varepsilon < \delta\),那么 \(T\) 是一个 \(X_{\varepsilon, \delta}\rightarrow X_{\varepsilon, \delta}\) 的映射。 - 现在计算:
![image]()
取 \(\varepsilon\) 使得 \(L\varepsilon < 1\),那么 \(T\) 是 \(X_{\varepsilon, \delta}\) 上的压缩映射。
- 首先,可以找到足够小的 \(\varepsilon, \delta\),使得
Theorem(局部解的存在性和唯一性)
- \(\vec F(\vec y,t):U\subset \R^n×\R \rightarrow \R^n\) 是连续 Lipschitz 函数,\(U\) 是开集,且点 \((\vec \xi,t_0)\) 在 \(U\) 中。对于足够小的 \(\varepsilon > 0\),在区间 \((t_0-\varepsilon,t_0+\varepsilon)\) 上存在唯一的函数 \(\vec y(t)\) 满足
![image]()
- Picard iteration: 解可以通过求 \(T\) 的迭代过程的极限得到,这个迭代叫做 Picard 迭代。
![]()
- Peano Existence Theorem:当 \(\vec F\) 连续但不 Lipschitz 时,局部解仍然存在,但不一定唯一。
Def
- locally Lipschitz:由上面的定理,我们发现 Lipschitz 条件可以弱化为局部 Lipschitz 条件。
3.2 Extension of solutions
在这一小节中,我们考虑局部解的延拓。
最大解区间
Proposition(如果两个区间上分别存在两个初始值问题的解,则解在区间之交上相同)
- \(\vec F(\vec y,t):U\subset \R^n×\R \rightarrow \R^n\) 是连续局部 Lipschitz 函数,\(U\) 是开集,且点 \((\vec \xi,t_0)\) 在 \(U\) 中。设 \(\vec y_i(t)\) 是区间 \((\alpha_i,\beta_i)\)(包含 \(t_0\))上的函数,\(i=1,2\),且均是方程
![image]()
的解,则 \(\vec y_1(t)=\vec y_2(t),max\{\alpha_1,\alpha_2\}<t<min\{\beta_1,\beta_2\}.\)
Theorem(最大解区间)
- \(\vec F(\vec y,t):U\subset \R^n×\R \rightarrow \R^n\) 是连续局部 Lipschitz 函数,\(U\) 是开集,且点 \((\vec \xi,t_0)\) 在 \(U\) 中,则存在 \(t_-<t_0<t_+\) 和函数 \(\vec y(t),t\in (t_-,t_+)\) 是方程
![image]()
的解,且是最大的,即:如果 \(\vec{\widetilde y}(t)\) 是另一个区间 \(I\ni x_0\) 上方程的解,则 \(I\subset (t_-,t_+)\) 且 \(\vec{\widetilde y}(t) = \vec y(t),t\in (t_-,t_+).\)
Proposition(局部条件下最大解不被紧集限制)
- \(\vec y(t)\) 是上述定义下 \((t_-,t_+)\) 上的最大解,假设 \(t_+<+\infty\),那么对任意紧集 \(K\subset U\),存在 \(\varepsilon >0\) 使得 \((\vec y(t),t)\notin K, t_+-\varepsilon<t<t_+\)。即,在一段时间后,最大解会跑出 \(K\) 的范围。
- 证明思路:
- 找一个更大的紧集 \(\widetilde K\) 和 \(\delta>0,\varepsilon >0\),使得
![]()
- 由于 \(\widetilde K\) 是紧集,\(\vec F\) 在 \(\widetilde K\) 中满足 Lipschitz 条件,且有界。
- 假设
![image]() ,由上一条,我们可以找到 \(\varepsilon\),使得 \(T\) 在 \((\tau-\varepsilon,\tau+\varepsilon)\) 上是压缩映射,那么方程
,由上一条,我们可以找到 \(\varepsilon\),使得 \(T\) 在 \((\tau-\varepsilon,\tau+\varepsilon)\) 上是压缩映射,那么方程 ![image]() 在 \((\tau-\varepsilon,\tau+\varepsilon)\) 上有解,但 \(\tau+\varepsilon>t_+\),矛盾!
在 \((\tau-\varepsilon,\tau+\varepsilon)\) 上有解,但 \(\tau+\varepsilon>t_+\),矛盾!
- 找一个更大的紧集 \(\widetilde K\) 和 \(\delta>0,\varepsilon >0\),使得
线性增长条件下的全局存在性
Lemma(Gronwall 不等式)
- \(f:[a,b]\rightarrow\R\) 连续且满足
![image]()
其中 \(k≥0,C\) 是常数,那么
![image]()
Proposition(线性增长条件下解全局存在)
- \(\vec F(\vec y,t):U\subset \R^n×\R \rightarrow \R^n\) 是连续局部 Lipschitz 函数,\(U\) 是开集。假设存在非负常数 \(k,C\) 使得
![image]()
那么初始值问题![image]()
的解对任意 \(t\in (-\infty,+\infty)\) 存在。另外,![image]()
- 证明思路:反证法,如果 \(t_+<+\infty\),则运用 Gronwall 不等式和上面的命题,解落在紧集里,矛盾!
3.3 Dependence on Initial Data
一个数学问题如果是适定问题(well-posed problem),那它需要满足三个条件:
- Existence 解存在:the problem has at least one solution.
- Uniqueness 解唯一:the problem has no more than one solution.
- Continuous dependence 解根据初始条件连续变化:the solution depends continuously on the data given.
现在我们已经研究了初始值问题的解的存在性和唯一性,在这节我们会研究解的连续变化性。
Continuous Dependence on Initial Value
Theorem(解关于初始值连续变化)
- \(\vec F(\vec y,t):U\subset \R^n×\R \rightarrow \R^n\) 是连续局部 Lipschitz 函数,\(U\) 是开集。设 \((\vec \xi_0,t_0)\in U\),\(\vec y_0(t)\) 是初始值问题 $$\frac{d\vec y_0}{dt}=\vec F(\vec y_0,t), \vec y_0(t_0) = \vec \xi_0$$ 的解,那么
- 对于任意的 \(\alpha<t_1<t_0<t_2<\beta\),存在 \(\vec \xi_0\) 的邻域 \(V\subset \R^n\) 使得初始值问题 $$\frac{d\vec y}{dt}=\vec F(\vec y,t), \vec y(t_0) = \vec \xi$$ 对任意 \(\vec \xi\in V\) 在 \((t_1,t_2)\) 上有解。
- 若把初始值问题 \(\vec y(t_0) = \vec \xi,\vec \xi \in V\) 的解记为 \(\vec y(t,\vec \xi)\),那么存在非负常数 \(L,M\),使得对任意 \(\vec \xi,\vec \xi' \in V\) 和 \(t,t' \in (t_1,t_2)\),有
![image]()
特别地,\(\vec y(t,\vec \xi)\) 在 \((t_1,t_2)×V\) 里 Lipchitz 连续。
- 证明思路:
- 取紧集 \(K\):
![image]()
由于 \(\vec F\) 局部 Lipschitz,它在 \(K\) 中关于 \(\vec yx\) Lipschitz,设 Lipschitz 数为 \(L\)。 - 取开球
![image]()
先考虑 \(\vec \xi\) 变化的情况。设 \([t_0,t_+)\) 是 \(\vec y(t_0)=\vec \xi\) 的最大解区间,令 \(g(t)=|\vec y(t) - \vec y_0(t)|, t_0 ≤ t < min(t_+,t_2)\),由积分方程、Lipschitz 条件和 Gronwall 引理,有![image]()
由 \(V\) 的取法,有 \(g(t)≤\delta\),因此解在紧集中,推出 \(t_+≥t_2\)(如果 \(t_+\) 有限,一段时间内解一定会跑出去,但是这里没有跑出去,说明 \(t_2\) 小;如果 \(t_+=+\infty\),即得),因此解 \(\vec y(t)\) 在 \([t_0,t_2)\) 上存在,且![image]()
- 积分:
![image]()
- 取紧集 \(K\):
Continuous Dependence on Parameters
\(\vec F\) 可能和参数 \(\vec \lambda\) 有关,可以表示为 \(\vec F(\vec y,t,\vec\lambda)\) 的形式,那么初始值问题
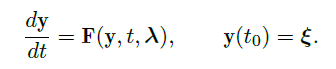
的解会与 \(\vec \xi\) 和 \(\lambda\) 同时相关。解这个问题可以转化为:解

Theorem(解关于参数连续变化)
Differentiability
在这一节,我们如果 \(\vec F\) 是 \(C^1\) 的,那么解关于初始值可导。我们先定性地分析解的形式。
设初始值问题 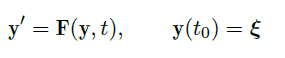
的解为 \(\vec y(t,\vec \xi)\),在 \(\vec \xi=\vec \xi_0\) 处的 \(\vec \xi_1\) 方向导数为: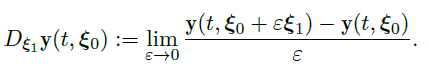
考虑 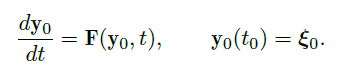 的解 \(\vec y_0(t)=\vec y(t,\vec \xi_0)\),令
的解 \(\vec y_0(t)=\vec y(t,\vec \xi_0)\),令 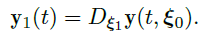 则
则
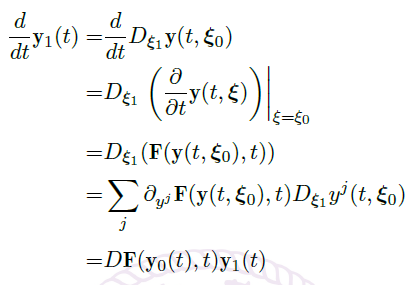
因此,\(\vec y_1(t)\) 是方程
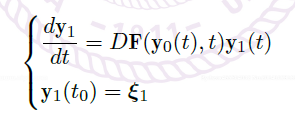
的解,其中 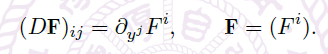
Theorem(解可微,大定理)
- 假设 \(\vec F(\vec y,t)\) 在 \(U\subset \R^n×\R\) 上是 \(C^1\) 的,\(\vec y_0(t)\) 是初始值方程
![image]() 在区间 \((\alpha,\beta)\ni t_0\) 上的解。
在区间 \((\alpha,\beta)\ni t_0\) 上的解。
对于足够小的 \(\varepsilon\),设 \(\vec y_1(t)\) 是方程
![image]()
的解,这里
![image]()
那么,当 \(t\in(t_1,t_2)\) 时,
![image]()
3.4 Analyticity
Def
- real analytic
Proposition(实解析的充要条件)
Theorem(Cauchy-Konvalevskaya, ODE version)
- 假设 \(f\) 在 \(y_0\) 的邻域 \(U\) 上实解析。\(y(t)\) 是初始值问题
![image]() 在区间 \((-\varepsilon,\varepsilon)\) 上的唯一解(\(\varepsilon\) 足够小),则 \(y(t)\) 在 \((-\varepsilon,\varepsilon)\) 上实解析。
在区间 \((-\varepsilon,\varepsilon)\) 上的唯一解(\(\varepsilon\) 足够小),则 \(y(t)\) 在 \((-\varepsilon,\varepsilon)\) 上实解析。 - 证明思路:
- 不妨设 \(y_0=0\)。利用方程不断微分,我每次进行 \(\frac{dy}{dt}=f(y)\) 的换元,我们可以得到存在一个独立于 \(f\) 的非负系数多项式 \(P_n\),使得
![image]()
- 我们想找函数 \(g\),满足:
- \(g\) 的各项导数非负且
![image]()
- 存在 \(u(t)\) 满足
![image]() ,且 \(u(t)\) 在 0 附近解析。
,且 \(u(t)\) 在 0 附近解析。
- \(g\) 的各项导数非负且
- 如果找到了 \(u,g\),有:
![image]()
由于 \(u(t)\) 在 0 附近解析,则幂级数![image]() 有正的收敛半径,因此
有正的收敛半径,因此 ![image]() 也有正的收敛半径且在 0 附近解析。
也有正的收敛半径且在 0 附近解析。 - 下证在 0 附近,\(T(t)=y(t)\)。只要证明 \(T\) 也是初始值问题的解,由解的唯一性即得。设
![image]() 因此
因此 ![image]()
得证。因此 \(y(t)=T(t)\),在 0 附近解析。 - 只要找 majorant function \(g\) 且证明 \(u(t)\) 在 0 附近解析。由前面的实解析充要条件,只需要选择
![image]() 即可,\(u(t)\) 可以直接计算得到。
即可,\(u(t)\) 可以直接计算得到。
- 不妨设 \(y_0=0\)。利用方程不断微分,我每次进行 \(\frac{dy}{dt}=f(y)\) 的换元,我们可以得到存在一个独立于 \(f\) 的非负系数多项式 \(P_n\),使得
Theorem(Cauchy-Kovalevskaya, ODE version’)
- 假设 \(f\) 在 \(y_0\) 的邻域 \(U\) 上解析。\(y(t)\) 是初始值问题
![image]() 在区间 \((-\varepsilon,\varepsilon)\) 上的唯一解(\(\varepsilon\) 足够小),则 \(y(t)\) 在 \((-\varepsilon,\varepsilon)\) 上解析。(实解析 to 解析)
在区间 \((-\varepsilon,\varepsilon)\) 上的唯一解(\(\varepsilon\) 足够小),则 \(y(t)\) 在 \((-\varepsilon,\varepsilon)\) 上解析。(实解析 to 解析)
Ch4 Power Series Solutions
终于熬过初值问题了……我给老师磕头了
- 在这一章中,我们研究一种线性 ODE
![image]()
它的系数在某些定义域上解析。我们可以把上述方程改写为
![image]()
并定义:- \(t_0\) 是方程的 ordinary point,如果所有的系数在 \(t=t_0\) 附近解析;
- 否则,称 \(t_0\) 是方程的 singular point。
- 相似的,我们研究一种线性系统
![image]()
ordinary point 和 singular point 的定义同上。 - 显然,\(t_0\) 是一个线性 ODE 的 ordinary point 当且仅当它是相关的一阶线性系统的 ordinary point。
4.1 Ordinary Point
我们从三个例子来看 Ordinary Point 方程怎么解:
Example 4.1.1
- 考虑初始值问题
![image]()
这里 \(p\) 是任意常数。 - 解决思路:
- 方程的系数解析,\(t=0\) 是一个 ordinary point。
- 在 \(t=0\) 附近,设
![image]()
代入,比较系数,解得
![image]()
Example 4.1.2(Legendre’s Equation)
- 考虑初始值问题
![image]()
这里 \(p\) 是任意常数。 - 解决思路:
- 把方程写为
![image]()
很明显,系数在 \(t=0\) 附近解析,因此原点是 ordinary point。 - 在 \(t=0\) 附近,设
![image]()
代入,比较系数,解得
![image]()
- 把方程写为
- 讨论:
- 当 \(p\) 不是整数时,每个括号里的数列有收敛半径 \(R=1\),这个可以由 ratio test 得到。这个函数被称为 Legendre function,它不是初等函数。
- 当 \(p\) 是整数时,其中的一个括号中的序列会中止,因此是一个多项式。满足 Legendre 方程的 \(n\) 阶多项式被称为 Legendre polynomial,它被显式地表示为
![image]()
Example 4.1.3(Airy Equation)
- 考虑方程
![image]()
- 解决思路:
原点是一个 ordinary point,设 \(y(t)\) 为幂级数,代入反解,得
![image]()
- 讨论:
- 这个方程叫做 Airy function。
- 方程的一个重要表达式是
![image]()
后续讨论略。
4.2 Linear System with Regular Singularity
我们研究线性系统:

在这节中,我们考虑 \(A(t)\) 有singularities 的情况。
Some Examples
Def
- regular singular point / a singularity of the first kind:对于线性系统
![image]() ,有
,有 ![image]() 且 \(B(t)\) 在 \(t=t_0\) 附近解析。
且 \(B(t)\) 在 \(t=t_0\) 附近解析。
- 不失一般性,我们可以假定 \(t_0=0\),那我们可以把 \(A(t)\) 写成如下形式:
![image]()
- 不失一般性,我们可以假定 \(t_0=0\),那我们可以把 \(A(t)\) 写成如下形式:
Example 4.2.2-4.2.3
- 考虑
![image]()
由分离变量法,可以解得 \(y=ct^b\),其中 \(c\) 是一个常数。 - 考虑
![image]()
若定义 \(t^B:=e^{B\ln(t)}\),则可以解得![image]() ,其中 \(\vec \xi\) 是一个常列向量。
,其中 \(\vec \xi\) 是一个常列向量。
- 若 \(B\) 可对角化,且
![image]()
那么
![image]()
因此,解的形式为
![image]()
如果我们改变变量,定义![image]()
那么原方程等价于
![image]()
进一步,等价于 n 个方程:
![image]()
- 如果 \(B\) 可以表示为 Jordan 块的形式:
![image]()
那么,可以计算
![image]()
这个矩阵给出了 \(\vec y(t)=e^{B\ln(t)}\vec \xi\) 的一个显式表达。可以注意到
![image]()
因此当特征值 \(\lambda>0\) 时,解 \(\vec y(t)\rightarrow 0,\ as\ t\rightarrow 0\),否则它最终会爆炸。
- 若 \(B\) 可对角化,且
Solutions in General
上述例子展示了这类方程的解的主要形态,一般的情况可以用我们接下来展示的方法简化到上面的情况。
Def(Gauge reansformation)
- Gauge transformation:对于元素是在 0 附近解析的函数,且行列式不等于 0 的矩阵 \(P(t)\),取 \(\vec y(t)\rightarrow \vec y(t)=P(t)\vec z(t)\),则原来的方程变为
![image]()
新的方程形式上保持一致,但是
![image]()
Lemma
- 如果 \(U,V\in M_n(\mathbb{C})\) 没有相同的特征值,那么线性映射
![image]()
是同构。
Proposition(特征值差不是正整数时,可以找到合适的 Gauge 变换)
- 假设 \(A(t)\) 在原点附近解析,令
![image]() 且假设 \(A_{-1}\) 没有两个特征值之间的差是正整数,那么存在 Gauge 变换 \(P(t)\),使得
且假设 \(A_{-1}\) 没有两个特征值之间的差是正整数,那么存在 Gauge 变换 \(P(t)\),使得
![image]()
- 证明思路:
- 设 \(P(t)=\Sigma_{k≥0}P_k t^k\) 是形式幂级数,我们先求系数,再证它收敛。
- 代入原方程,需要:
![image]()
取 \(P_0 = I_n\)。由于 \(A_{-1}-kI_n(k>0)\) 和 \(A_{-1}\) 没有相同的特征值,由 Lemma,我们可以找到唯一的 \(P_k\),这样就找到了 \(P(t)\)。 - 证 \(P(t)\) 在 \(t=0\) 附近解析略。
Solutions in General 通解
下面我们来讨论一般情况下如何解决  ,其中
,其中 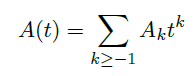
- 如果 \(A_{-1}\) 没有两个特征值差为正整数,由上面的 Proposition,可以找到一个 Gauge 变换
![image]() ,且 \(\vec z(t)\) 满足
,且 \(\vec z(t)\) 满足 ![image]()
由 Example 4.2.3,有
![image]()
其中 \(\vec \xi\) 是常向量。 - 如果 \(A_{-1}\) 有两个特征值差为正整数,设 \(A_{-1}\) 的 Jordan 标准型为
![image]()
我们考虑替换变量:\(\vec y(t)=Q(t)\vec z(t)\),其中
![image]()
由于 \(Q(t)^{-1}\) 在 \(t=0\) 时为奇点,因此它不是一个 Gauge 变换。但我们仍然可以得到
![image]()
其中
![image]()
且如果把 \(B(t)\) 写成幂级数的形式,那么 \(B_{-1}\) 是这个形式:
![image]()
可以看到特征值的差减小了1。我们可以再把 \(B_{-1}\) 变换成 Jordan 标准型,并重复以上的操作,最终可以到达前一种情况。
4.3 Scalar Equation with Regular Singularity
在这一节中,我们考虑 n 阶标量线性方程:
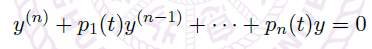
Regular Singularity
Def
- regular singularity:\(t=t_0\) 是 singular point 并且 \((t-t_0)^kp_k(t)\) 在 \(t=t_0\) 附近解析(对 \(p_k(t)\) 来说,极点的阶最多是 \(k\) 阶);irregular
The Method of Frobenius
我们关注以 \(t=0\) 为 regular singularity 的二阶线性方程 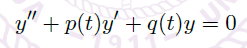
- 取 indicial polynomial 指标多项式
![image]()
其中,\(p_0=lim_{n\rightarrow \infty}tp(t),q_0=lim_{n\rightarrow \infty}t^2q(t)\)
下分两种情况讨论:- 如果 \(f(\lambda)\) 有两个不同的根 \(m_1,m_2\) 且 \(m_1-m_2\notin \Z\),那我们可以找到方程的两个线性独立的 Frobenius 级数解:
![image]()
- 如果 \(f(\lambda)\) 有两个不同的根 \(m_1<m_2\) 且 \(m_1-m_2\) 是正整数,那么我们至少有一个 Frobenius 级数解,形式为
![image]()
- 如果 \(m_1=m_2\),则我们只有一个 Frobenius 级数解。
- 如果 \(f(\lambda)\) 有两个不同的根 \(m_1,m_2\) 且 \(m_1-m_2\notin \Z\),那我们可以找到方程的两个线性独立的 Frobenius 级数解:
- 把级数解代入,比较系数即可解得。
Example(Hypergeometric Series)
- 考虑下面的例子:
![image]()
我们可以把它写成
![image]()
- 由上面的方法,可以有一个解
![image]()
- 我们一般把 hypergeometric series 记为 \(F(a,b,c,t)\),\(F(1,b,b,t)=\frac{1}{1-t}\) 生成了一般的 geometric series。
- 如果 \(1-c\) 不是整数,我们会有第二个解
\(y=t^{1-c}z,\)
![image]()
因此,如果 \(c\) 不是整数,解的一般形式为
![image]()
Ch5 Boundary Value Problem
5.1 Boundary Value Problem for Second Order Equations
我们先研究二阶线性方程
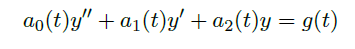
它的系数在区间 \(I=[a,b]\) 上连续且恒不等于0.
Def(边界条件)
- 三种边界条件
- Dirichlet boundary conditions (第一类边界条件)
![image]()
- Neumann boundary conditions(第二类边界条件)
![image]()
- Robin boundary conditions(第三类边界条件)
![image]()
- Dirichlet boundary conditions (第一类边界条件)
- 注:和初始值问题不同,边界值问题的解有可能不存在或不唯一。
Boundary Value Problem of Sturmian Type
Def(Sturm-Liouville Form)
- Sturm-Liouville Form / self-adjoint form:我们可以把方程改写成下面的形式
![image]()
- Sturm-Liouville operator:
![image]()
- 证明思路:
- 把方程两边同时乘上
![image]()
- 方程变为:
![image]()
其中,
![image]()
- 在计算中,我们还可以发现 \(p(t)\) 是连续可微的,且在 \(I\) 上为正。
- 把方程两边同时乘上
Def(Boundary Value Problem of Sturmian Type)
- 接下来,我们关注边界值问题 (S)
![image]()
其中 \(p(t)\in C^1(I),\ p(t)>0,\ q(t),f(t)\in C^0(I)\),且 \(\alpha_i,\beta_i,\xi_i\in \R,\ (\alpha_1,\beta_1)\neq(0,0),\ (\alpha_2,\beta_2)\neq(0,0)\)
Proposition(Lagrange Identity)
- 对任意 \(u(t),v(t)\in C^2(I)\),有
![image]()
其中 \(L\) 是 Sturm-Liouville 算子。
Proposition
- 假设 \(B_iu=B_iv=0,(i=1,2)\),那么
![image]()
齐次问题
我们先考虑齐次问题 (H)
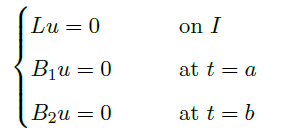
这样,边界值问题 (S) 的解可以表示为特解和齐次问题的通解之和。
Theorem(非齐次可解且解唯一 \(\Leftrightarrow\) 齐次只有零解)
- 非齐次边界值问题 (S) 唯一可解 \(\Leftrightarrow\) 齐次问题 (H) 只有零解。
- 证明思路:
- 先考虑方程 \(Lu=0\),它有两个线性独立的解,因此所有解可以表示成它们的线性组合 \(u(t)=c_1u_1(t)+c_2u_2(t),c_i\in\R\)
- 为了满足边界条件,我们把边界条件转换为矩阵乘法形式,可以得到系数矩阵
![image]() 是可逆的,同理转换为矩阵乘法形式,非齐次边界值问题有唯一解。
是可逆的,同理转换为矩阵乘法形式,非齐次边界值问题有唯一解。
- 因此,非齐次边界值问题 (S) 的唯一可解性等价于
![image]()
其中,\(u_1,u_2\) 为 \(Lu=0\) 的两个线性独立的解。
5.2 Green’s Function for Second Order Equations
在上一节中,我们发现解带有边界条件 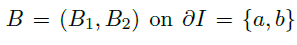 的方程
的方程
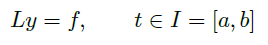
的方法很像线性代数中矩阵方程的解法。由方程 \(Ly=f\),我们希望构造 \(L^{-1}\),使得 \(y=L^{-1}f\)。
事实上,通过构造 Green 函数 \(G(t,s)\),我们可以得到方程的解
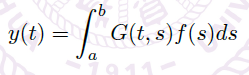
Green's Function
Def
- Green's function \(G(t,s)\):
![image]()
其中,![image]()
\(u_1\) 是
![image]()
的解,\(u_2\) 是
![image]()
的解。
Proposition(Green 函数的性质)
- \(G(t,s)\) 有以下性质:
- 它在 \((t,s)\in I×I\) 上连续。
- \(G(t,s)=G(s,t)\).
![image]() 存在且在远离 \(t=s\) 处连续。
存在且在远离 \(t=s\) 处连续。- 在对角线 \(t=s\) 处,单侧极限
![image]()
存在且差为
![image]()
- 令
![image]()
分别代表在 \(t\) 和 \(s\) 处的 Sturm-Liouville 算子,那么
![image]()
用 Green's Function 表示的解
Theorem(半齐次方程的唯一解)
- 如果齐次方程 (H) 只有零解,那么下面的半齐次边界值方程
![image]()
有唯一解
![image]()
- 对于一般情况
![image]()
我们可以先找到
![image]()
的通解 \(u=c_1u_1+c_2u_2\),那么以上方程可以变为半齐次情况
![image]()
因此
![image]()
5.3 Boundary Value Problem in General
我们考虑一阶线性系统的边界值问题
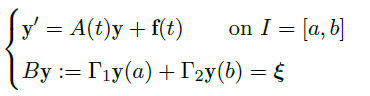
其中 \(\vec y(t)\) 是 \(n\) 个未知函数构成的列向量,\(A(t)\) 是一个在 \(I\) 上随着 \(t\) 连续变化的 \(n\) 阶矩阵,\(\Gamma_1,\Gamma_2\) 是 \(n\) 阶常矩阵,\(\xi\) 是常列向量。
Theorem(一阶线性系统唯一可解 \(\Leftrightarrow\) 齐次系统有唯一解)
- 非齐次边界值问题
![image]() 在区间 \(I\) 上唯一可解 \(\Leftrightarrow\) 齐次边界值问题
在区间 \(I\) 上唯一可解 \(\Leftrightarrow\) 齐次边界值问题 ![image]() 在 \(I\) 上只有零解。
在 \(I\) 上只有零解。
Def(Green's matrix)
- Green's matrix:
![image]()
- 边界值问题
![image]()
的解为
![image]()
5.4 Compact Self-adjoint Operators
Def
- inner product space 内积空间:线性 \(\R\ or\ \C\),装备了内积
![image]() ,满足:
,满足:
- 对称性:\((f,g)=\overline{(g,f)}\)
- 线性:\((\alpha f+\beta g,h) = \alpha (f,h)+\beta (g,h)\)
- 正:\((f,f)>0\ for\ f\neq 0\)
- 内积空间是一个赋范空间(normed space),向量 \(f\in H\) 的范数的定义为
![]()
Def
- Hilbert space:一个内积空间称为 Hilbert 空间,如果它作为赋范空间是完备的。(Banach 空间:赋范线性空间;Hilbert 空间:赋范线性内积空间)
Def
- \(H\) 是内积空间,\(T:H\rightarrow H\) 是一个线性算子。\(T\) 被称为:
- bounded 有界,如果范数
![]()
是有限的。 - self-adjoint 自伴随:如果
![]()
- compact 紧:如果对任意有界序列 \(\{f_n\}\subset H\),序列 \(\{Tf_n\}\) 在 \(H\) 中有收敛子列。
- 紧算子是有界的。
- 对有界算子 \(T\),有
![]()
- bounded 有界,如果范数
Proposition(有界自伴随算子的性质)
- 如果 \(T\) 是有界自伴随算子,那么 \((Tf,f)\in \R\) 且
![]()
Def
- eigenvalue 特征值 \(\lambda\),eigenvector 特征向量 \(f\):\(Tf=\lambda f,f\neq 0\)
Proposition(紧自伴随算子特征值不等式)
- \(T\) 是内积空间 \(H\) 中的紧自伴随算子,那么
![image]()
且存在特征值使等号取到。
Def
- orthonormal sequence 正交列:\(\{\phi_n\}_{n=0}^{\infty}\) 且 \((\phi_n,\phi_m)=\delta_{nm}\)
- the Fourier series 傅里叶级数:
![image]()
- the Forier coefficients 傅里叶系数:\(c_k\)
Proposition(Bessel 不等式)
- 设
![image]() 是 \(f\in H\) 的傅里叶级数,那么
是 \(f\in H\) 的傅里叶级数,那么
![]()
等号成立当且仅当![]()
Theorem
- \(H\) 是一个无限维内积空间,\(T\) 是紧自伴随算子,那么存在可数个实特征值 \(|\lambda_0|≥|\lambda_1|≥|\lambda_2|≥...\) 且 \(\lambda_n \rightarrow 0\ as\ n\rightarrow +\infty\)
相应的特征向量 \(\{\phi_n\}_{n=0}^{\infty}\) 是一个正交列,且 \(T\) 的像的每一个元素都可以用它的傅里叶级数表示
![]()
进一步,\(T\) 的任何非零特征值等于某个上面提到的 \(\lambda_i\)。 - 证明思路:
- 由之前的定理,可以取到特征值使得
![]() ,取对应的特征向量,则有
,取对应的特征向量,则有
![]()
- 考虑
![]() ,可以证 \(T:H_1\rightarrow H_1\),且是紧自伴随算子,那么可以再取出特征值 \(\lambda_1\) 和特征向量 \(\phi_1\),……一直取下去,就可以获得一个正交序列。
,可以证 \(T:H_1\rightarrow H_1\),且是紧自伴随算子,那么可以再取出特征值 \(\lambda_1\) 和特征向量 \(\phi_1\),……一直取下去,就可以获得一个正交序列。 - 放缩,即可得到傅里叶级数表示。
- 如果存在非零特征值和特征向量不在之前取出的特征值里面,可以推出特征向量为零,矛盾!因此所有非零特征值都被取到过。
- 由之前的定理,可以取到特征值使得
5.5 Sturm-Liouville Eigenvalue Problem
Sturm-Liouville 特征值问题:
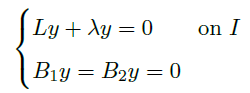
\(\lambda\) 取某些值的时候,可以找到非平凡的解,我们把这些 \(\lambda\) 叫做特征值。如果解空间是 \(m\) 维的,那我们称这个特征值为 \(m\) 重的(has multiplicity \(m\))。
我们总是假设齐次边界值问题只有平凡解,这等价于 \(\lambda=0\) 不是特征值。
Green’s function as Compact Self-adjoint Operator
- 记算子
![]() 为
为 ![]()
那么上述特征值边界值问题等价于
![]()
相应的解是算子 \(T\) 的特征向量。
下证 \(T\) 是一个紧自伴随算子。
Proposition(\(T\) 是紧自伴随算子)
- \(T\) 是 \(C(I)\) 上的紧自伴随算子。
解法
- 由上面的命题,可以得到一组正交序列 \(\{\phi_n\}_{n=0}^{\infty}\),则 Green 函数
![]()
可以解得
![]()
Ch6 Calculus of Variations 变分法
6.1 Euler-Lagrange Equation
Principle of Least Action 最小作用量原理
Def
- the Kinetic energy:\(K=\frac{1}{2}m\dot{\vec q}^2\)
- conservative force:\(\vec F(\vec q)=-\nabla V(\vec q)\) for some function \(V:\R^n\rightarrow \R\) called the potential
- the total Energy:\(E=K+V\)
Proposition(总能量守恒)
- 总能量 \(E\) 在运动过程中是守恒的。
- 证明思路:总能量对时间求导即证。
Def(拉格朗日量)
- Lagrangian:\(\mathcal L=K-V\)
- action functional:\(S[\vec q(t)]=\int^{t_1}_{t_0}\mathcal L(q_i,\dot q_i)dt\) for any path \(\vec q(t):[t_0,t_1]\rightarrow \R^n,\vec q(t)=(q_1(t),...,q_n(t))\)
Theorem(Principle of Least Action)
- 经典粒子的运动轨迹是系统的 action functional 在路径(path)空间里的极值点。
- 通常情况下(但并不总是),轨迹是最小值点。
Euler-Lagrange Equation
Theorem(Euler-Lagrange Equation)
- 假设 \(x(t):[t_0,t_1]\rightarrow \R\) 是一条光滑的路径,且是 action functional 在首、尾和 \(x(t)\) 相同的光滑路径中的极值点,那么 \(x(t)\) 满足 Euler-Lagrange Equation:$$\frac{d}{dt}(\frac{\partial \mathcal L}{\partial \dot x})=\frac{\partial \mathcal L}{\partial x}$$
- 证明思路:考虑 \(f(s):=S[x(t)+s\gamma (t)]\),其中 \(\gamma (t)\) 是一条首尾都是 \(0\) 的路径,则 \(f(s)\) 在 \(0\) 处取极值 \(\Rightarrow f'(0)=0\),计算并利用 \(\gamma (t)\) 的任意性即得 E-L 方程。
- n 维情况: $$\frac{d}{dt}(\frac{\partial \mathcal L}{\partial \dot{q_i}})=\frac{\partial \mathcal L}{\partial q_i}, i=1,2,...,n$$
其中 $$\vec q(t):[t_0,t_1]\rightarrow \R^n, \vec q(t)=(q_1(t),...,q_n(t))$$
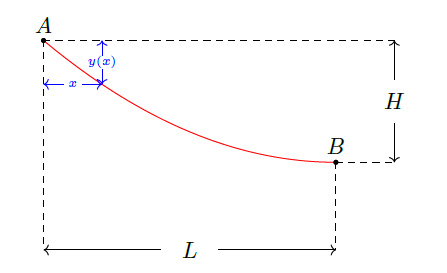
6.2 Brachistochrone Problem 最速降线问题
Brachistochrone Curve
问题
- 在垂直平面上给定两点 \(A\) 和 \(B\),仅在重力的作用下,使得从 \(A\) 运动到 \(B\) 的时间最短的路径是什么?
解答
-
对于任意的从 \(A\) 到 \(B\) 的路径 \(\gamma\),我们如下参数化:
![]()
- 动能 \(K=\frac{1}{2}mv^2\)
- 重力势能 \(V(x)=-mgy(x)\)
由能量守恒,有 \(K+V=0\Rightarrow v=\sqrt{2gy}\)
-
沿着 \(\gamma\) 降落的总时间为
![]()
其中![]()
计算得![]()
-
\(T[y(x)]\) 可以被视为 \(y(x)\) 的一个 functional(泛函?),把它视为带拉氏量
![]() 的 action functional,由 E-L 方程得:
的 action functional,由 E-L 方程得:
![]()
-
考虑 Legendre transform 勒让德变换,记 Hamiltonian 哈密顿量 \(\mathcal H = \frac{\partial \mathcal L}{\partial y'}y'-\mathcal L\),计算得 E-L 方程等价于 \(\frac{d}{dx}\mathcal H = 0\),推出 \(\mathcal H=C_1\) 是常数。
- well-known statement:如果拉格朗日量对时间没有明确的依赖,那么哈密顿量在运动中是守恒的。
-
因此,原方程等价于
![]()
解得![]()
Fermat's Principle 费马原理
- 光沿时间最短的路径传播。
Example(Snell's law)
![]()
- 等价表述:\(\frac{sin\theta}{v}=constant\)
应用
6.3 Isoperimetric Problem 等周问题
Action Principle with Constraint
the method of Lagrange multiplier 拉格朗日乘子法
- 我们想找满足约束 \(g(x,y)=0\) 的 \(f(x,y)\) 的极值点,引入新变量(Lagrange
multiplier) \(\lambda\),记 \(F(x,y,\lambda)=f(x,y)+\lambda g(x,y)\),则极值点满足
![]()
Theorem(带约束的最小作用量原理)
- 满足约束条件
![]() 的情况下,使得 action functional
的情况下,使得 action functional ![]() 最小的路径 \(x(t)\) 满足
最小的路径 \(x(t)\) 满足
![]()
其中 \(\mathcal L_\lambda = \mathcal L+\lambda \mathcal R\) - 多变量情况:
![]()
Isoperimetric Problem
问题
解答
- 带乘子的拉氏量为
![]()
- E-L 方程为
![]()
- 解得
![]()
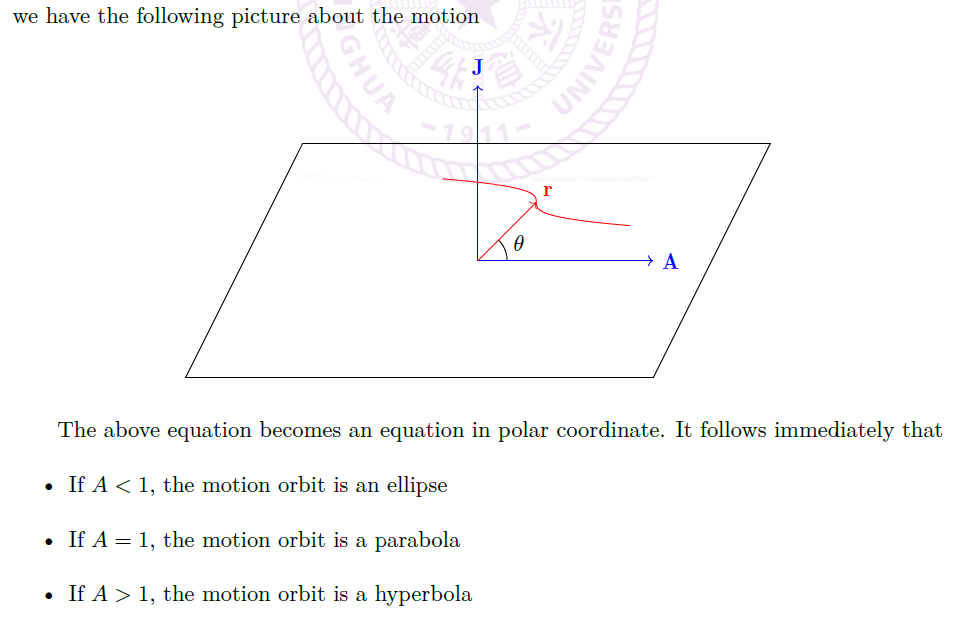
6.4 Kepler Problem
Solutions of Motion
问题
- 经典开普勒问题描述了具有势能 \(V(r)=-\frac{K}{r}\) 的物体在 \(\R^3\) 空间中的运动。
- 其中,\(\vec r=(x_1,x_2,x_3), r=\sqrt{x_1^2+x_2^2+x_3^2}\) 分别表示位置和长度
- \(\vec F=-\nabla V = - \frac{K}{r^2}\frac{\vec r}{r}\) 是一个与 \(r\) 成平方反比的保守力
- 下文中,我们只考虑 \(K>0\) 的情况,因此力为吸引力
解答
- 由牛顿第二定律,方程为 \(m\ddot{\vec r} = - \frac{K}{r^2}\frac{\vec r}{r}\)
- 角动量 \(\vec J=m\vec r\times \dot{\vec r}\) 守恒,且 \(\vec J \cdot \vec r = 0,\vec J \cdot \dot{\vec r} = 0\)
- Laplace-Runge-Lenz vector 拉普拉斯-龙格-楞次矢量 \(\vec A = \frac{\dot{\vec r}\times \vec J}{K}-\frac{\vec r}{r}\) 守恒
- 由 \(\vec A\cdot \vec r = Arcos\theta = \frac{J^2}{Km}-r \Rightarrow r = \frac{J^2}{Km}\frac{1}{1+Acos\theta}\)
讨论:
![image]()
Kepler's Laws
Kepler's First Law
- 由 \(\vec A\cdot \vec A = 1+\frac{2J^2E}{mK^2}\),其中 \(E=\frac{1}{2}m\dot{\vec r}^2-\frac{K}{r}\) 知
![image]()
Kepler’s Second Law
- \(\frac{dArea}{dt}=\frac{J}{2m}\) 是常量
Kepler’s Third Law
- 记 \(\tau = \frac{2m\pi ab}{J}\),则有 \((\frac{\tau}{2\pi})^2 = \frac{ma^3}{K} = \frac{a^3}{GM}\)
![image]()


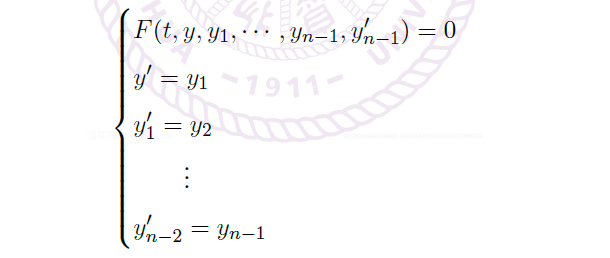
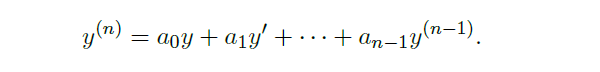
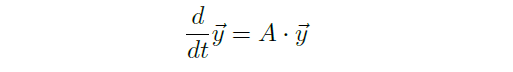
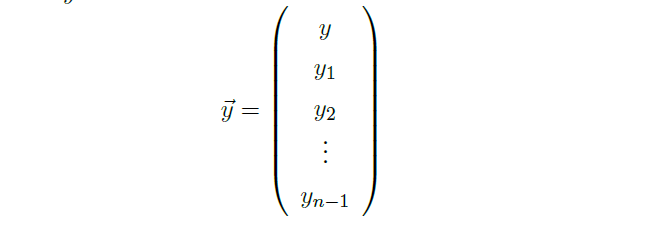
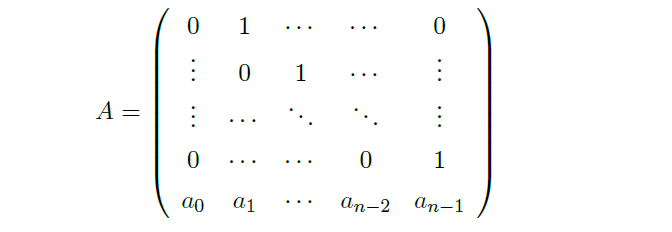
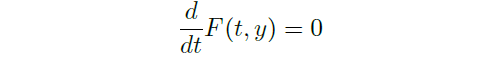
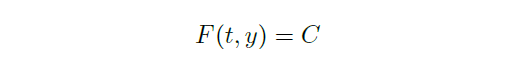
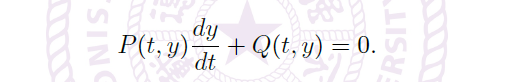
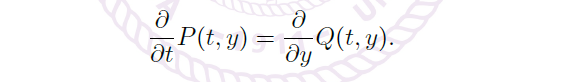
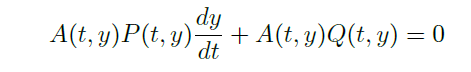
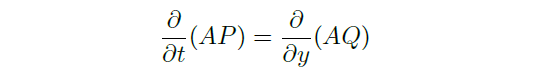
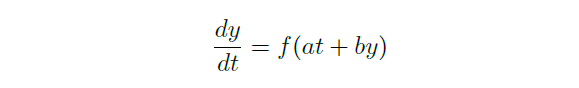
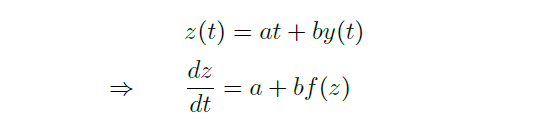
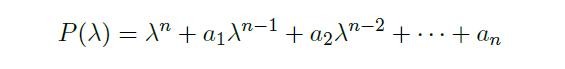
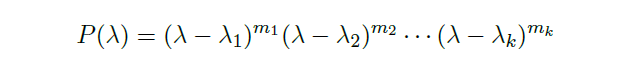
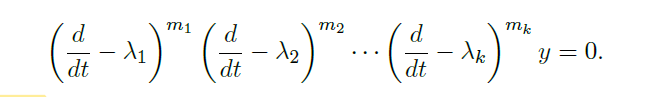
 是方程
是方程  的 n 个线性独立的解。
的 n 个线性独立的解。
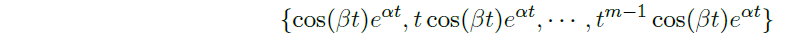
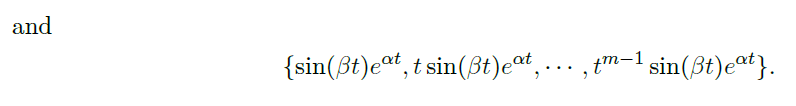

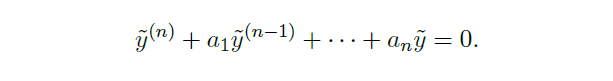
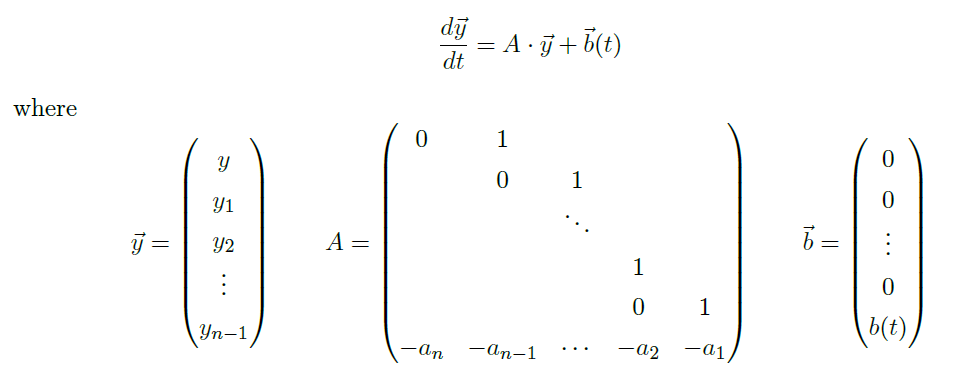
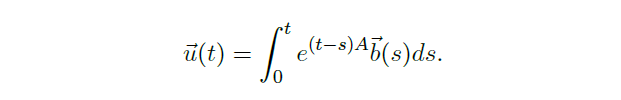


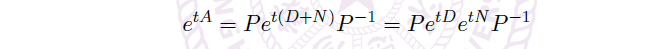

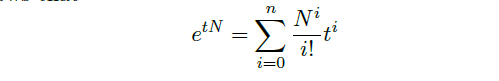
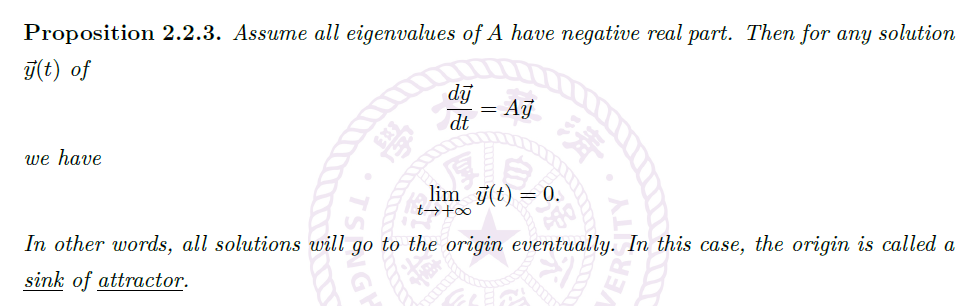
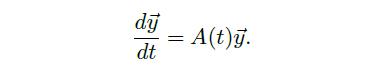
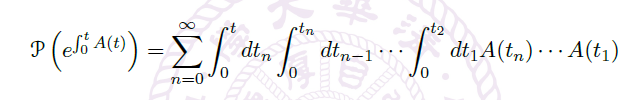

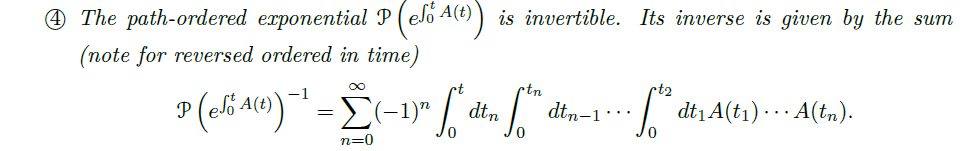
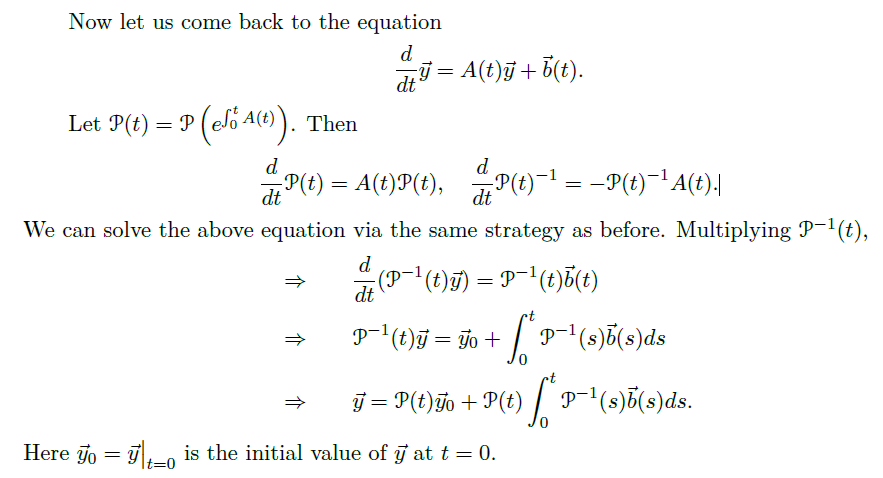
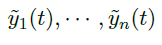
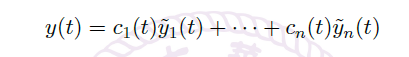
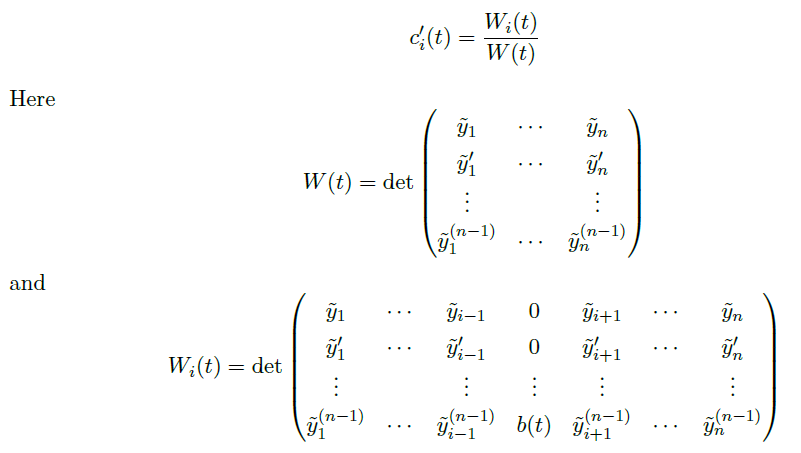

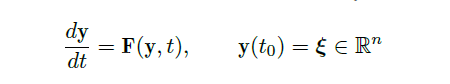
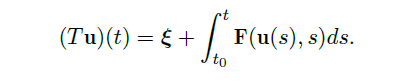
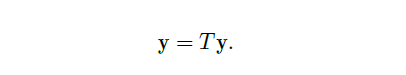

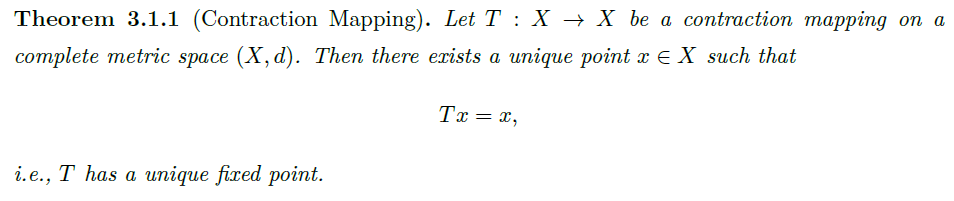

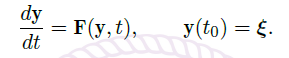 中,假设
中,假设 
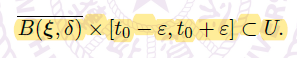
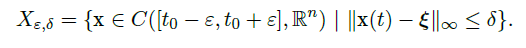 是一个以常函数
是一个以常函数 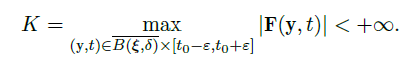
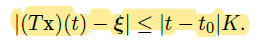

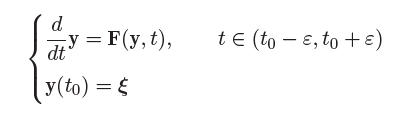


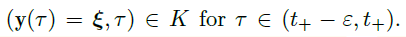 ,由上一条,我们可以找到
,由上一条,我们可以找到  在
在 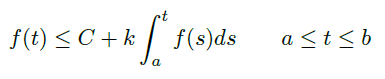

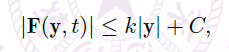
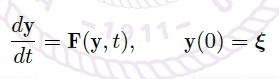

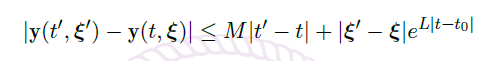

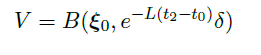

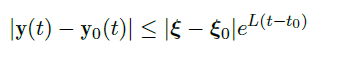
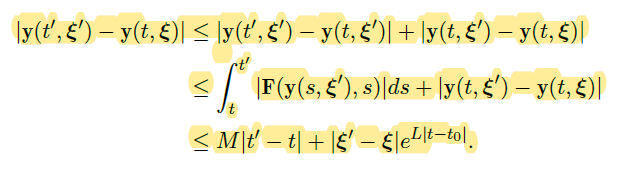

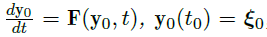 在区间
在区间 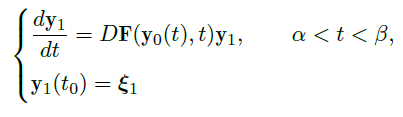
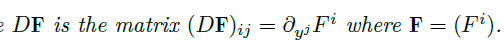
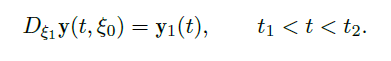
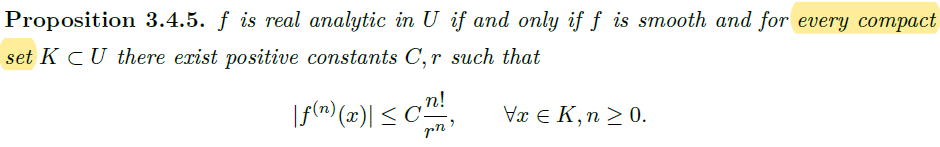
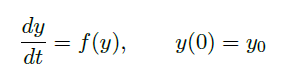 在区间
在区间 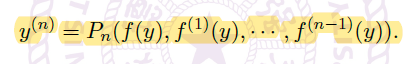
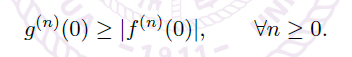
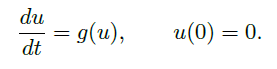 ,且
,且 
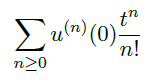 有正的收敛半径,因此
有正的收敛半径,因此 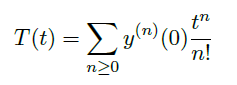 也有正的收敛半径且在 0 附近解析。
也有正的收敛半径且在 0 附近解析。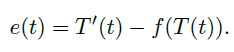 因此
因此 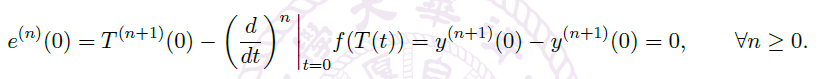
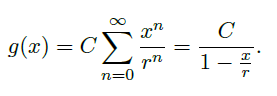 即可,
即可,
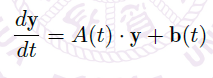
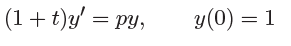
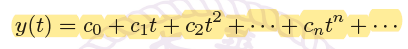
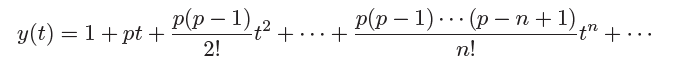
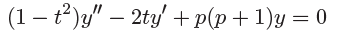
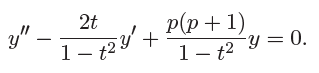
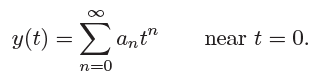

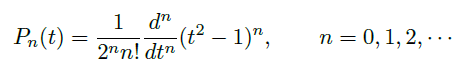
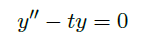

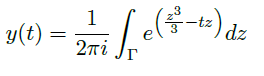
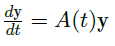 ,有
,有 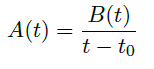 且
且 

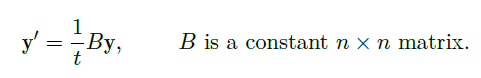
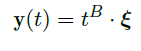 ,其中
,其中 
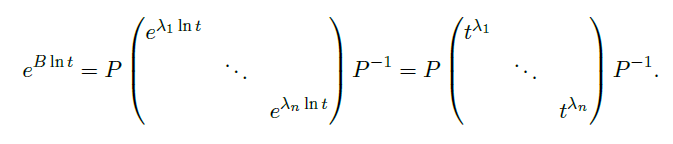
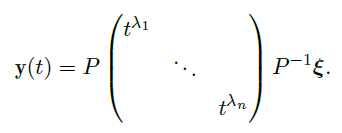
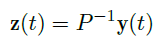
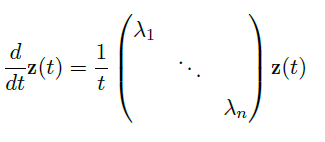
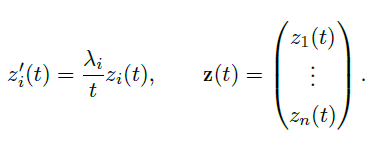
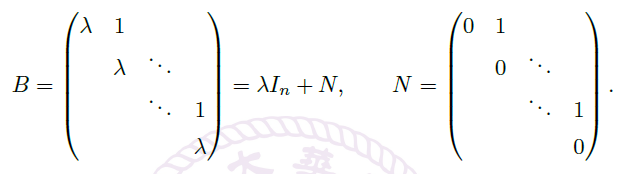

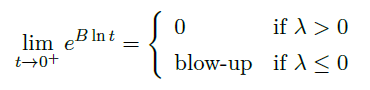
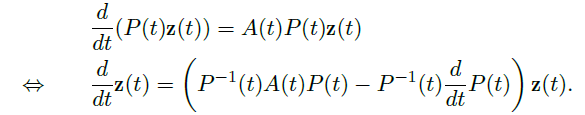
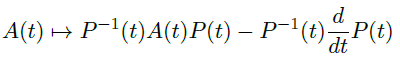
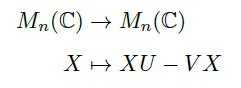
 且假设
且假设 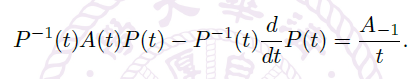
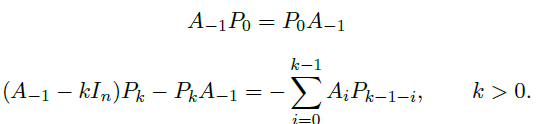
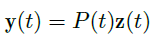 ,且
,且 



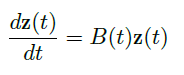
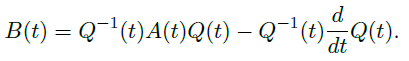
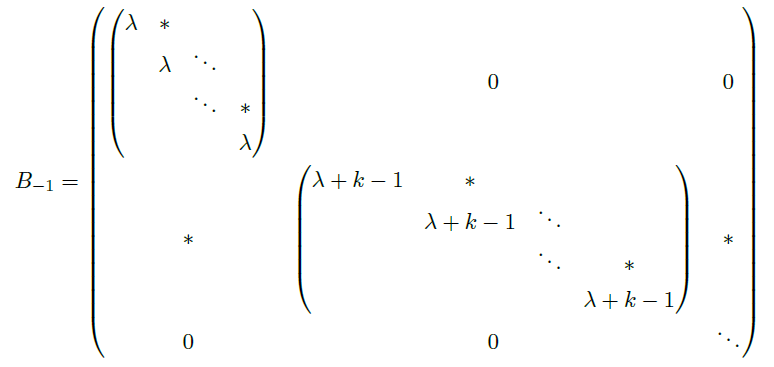
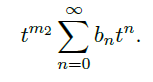
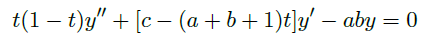
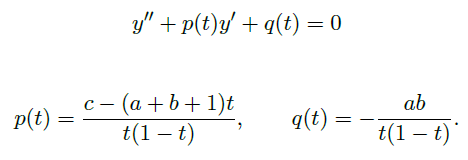
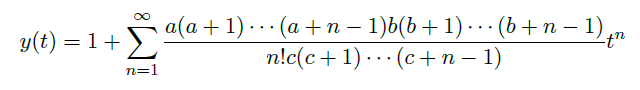

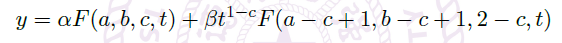



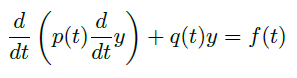
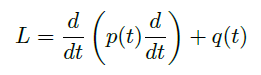
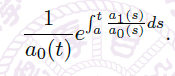
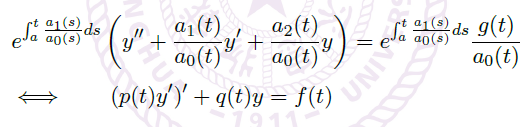
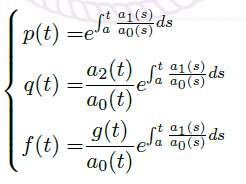
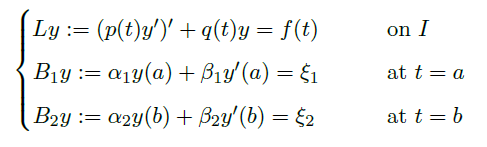
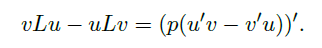
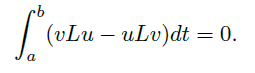
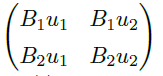 是可逆的,同理转换为矩阵乘法形式,非齐次边界值问题有唯一解。
是可逆的,同理转换为矩阵乘法形式,非齐次边界值问题有唯一解。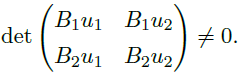
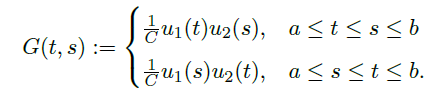
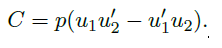

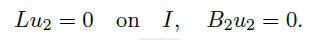
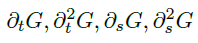 存在且在远离
存在且在远离 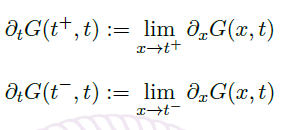
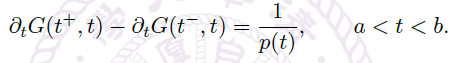
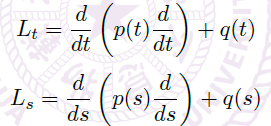
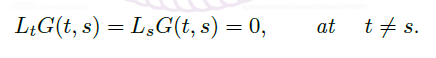
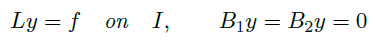


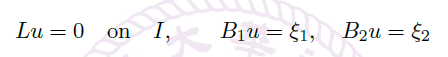

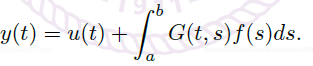
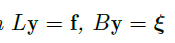 在区间
在区间  在
在 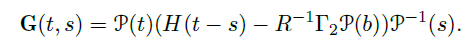


 ,满足:
,满足:
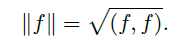
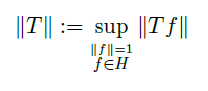
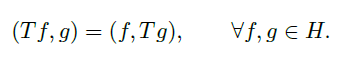
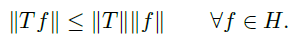


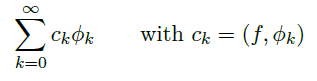
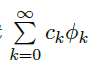 是
是 
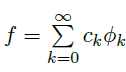
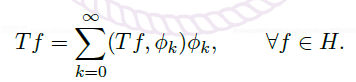
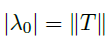 ,取对应的特征向量,则有
,取对应的特征向量,则有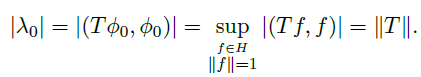
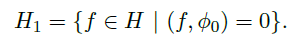 ,可以证
,可以证 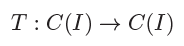 为
为 
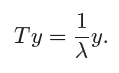

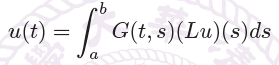
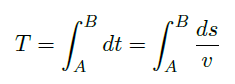
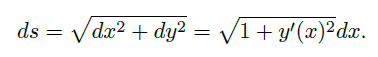
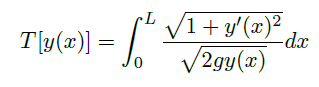
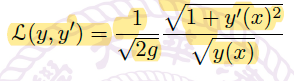 的 action functional,由 E-L 方程得:
的 action functional,由 E-L 方程得: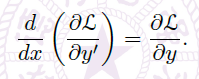
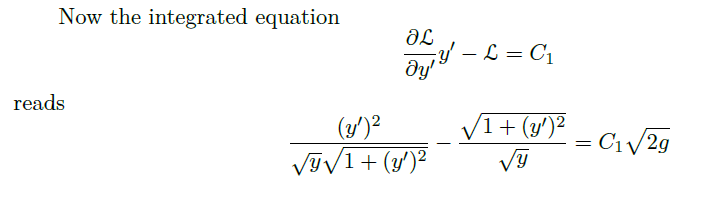
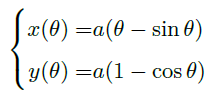

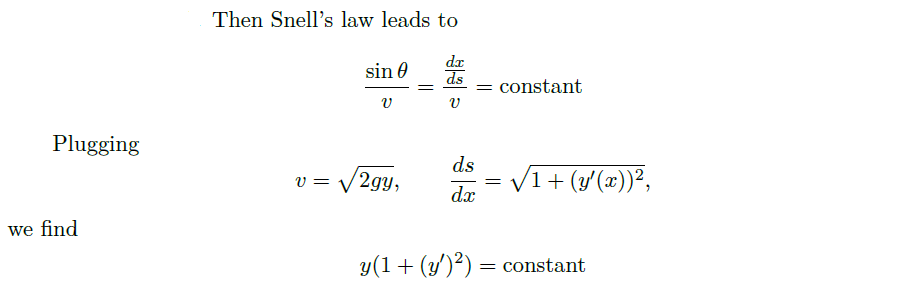
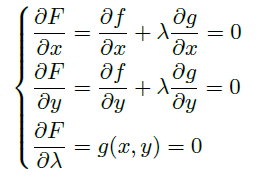
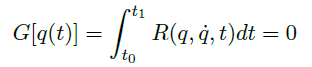 的情况下,使得 action functional
的情况下,使得 action functional 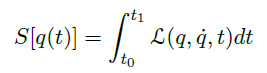 最小的路径
最小的路径 
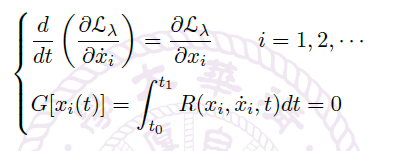
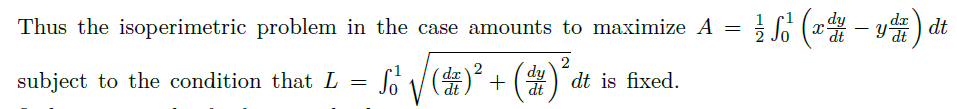
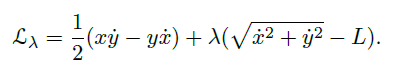
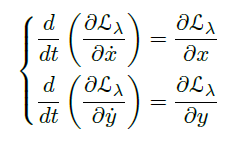
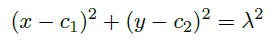


 浙公网安备 33010602011771号
浙公网安备 33010602011771号