算法实践报告第五章

0.“最小重量机器设计问题”问题描述

设某一机器由n个部件组成，每一种部件都可以从m个不同的供应商处购得。设

输入格式:

第一行有3 个正整数n ，m和d， 0<n<30, 0<m<30, 接下来的2n 行，每行n个数。前n行是c，后n行是w。

输出格式:

输出计算出的最小重量，以及每个部件的供应商

输入样例:

输出样例:

在这里给出相应的输出。例如：

4
1 3 1

代码描述:

#include <iostream>
using namespace std;

int n, m, d;    //总价格不超过d是剪枝条件, 选择方式和皇后一样，一行机器选择一列供应商
int c[30][30];
int w[30][30];
int nowweight;
int minweight = 1000000;
int cost;
int x[30];    //用来记录当前所选的供应商
int y[30];    //用来记录最终确认时所选的供应商

// bool place(int t){    //超时了 注销掉试试
//     for(int i=1; i<t; i++){    //第一次运行结果是结果是132 应该是131，说明剪枝剪得不够？不应该再到后面
//         if(cost + c[t][i] > d) //&& x[t] == x[i] )    //cost加上选择的机器对应价格应该小于 供应商可以与之前的选择重合！
//             return false;
//     }
//     return true;
// }

void Backtrack(int t){
    if(t>n){    //当到达叶子结点时更新最小机器值
        if(minweight > nowweight){
            minweight = nowweight;
            for(int i=1; i<=n; i++){    //更新最小值的同时也更新一下储存的供应商
                y[i] = x[i];
            }
        }
    }
    for(int i=1; i<=m; i++){
        if(nowweight + w[t][i] < minweight && cost + c[t][i] <= d){    //剪枝，只有当前的重量仍小于最小值才有必要加下一个值
            x[t] = i;    //t行对应选择的是第i个（列）供应商
            nowweight += w[t][i];
            cost += c[t][i];
//             if(place(t))
            Backtrack(t+1);
            nowweight -= w[t][i];
            cost -= c[t][i];
        }
    }
}

int main(){
    cin>>n>>m>>d;
    for(int i=1; i<=n; i++){
        for(int j=1; j<=m; j++){
            cin>>c[i][j];
        }
    }
    for(int i=1; i<=n; i++){
        for(int j=1; j<=m; j++){
            cin>>w[i][j];
        }
    }
    nowweight = 0;
    cost = 0;
    Backtrack(1);
    cout<<minweight<<endl;
    for(int i=1; i<=n; i++){
        cout<<y[i]<<" ";
    }
    return 0;
}

1.请用回溯法的方法分析“最小重量机器设计问题”

c[30][30]用来储存每一个零件的价格，w[30][30]用来储存每一个零件的重量

nowweight用来记录当前记录的总重量，minweight用来记录最小重量，cost用来记录价格

用x[30]数组来记录当前所选的供应商，用y[30]数组来记录最终所选的供应商

当循环到叶子结点时判断每个节点状态，根据比大小来确定是否需要更新minweight以及对应的y数组

通过将已加的值在改支线已到达叶子节点（即三个零件都进行选择）后回溯到之前的值再走另一支路

同时需要选择使用剪枝函数判断当前所加价格是否超出d，可以加快回溯的效率

1.1说明“最小重量机器设计问题"的解空间

（1，1，1）（1，1，2）（1，1，3）（1，2，1）（1，2，2）（1，2，3）（1，3，1）

（1，3，2）（1，3，3）（2，1，1）（2，1，2）（2，1，3）（2，2，1）（2，2，2）

（2，2，3）（2，3，1）（2，3，2）（2，3，3）（3，1，1）（3，1，2）（3，1，3）

（3，2，1）（3，2，2）（3，2，3）（3，3，1）（3，3，2）（3，3，3）

1.2说明 “最小重量机器设计问题"的解空间树

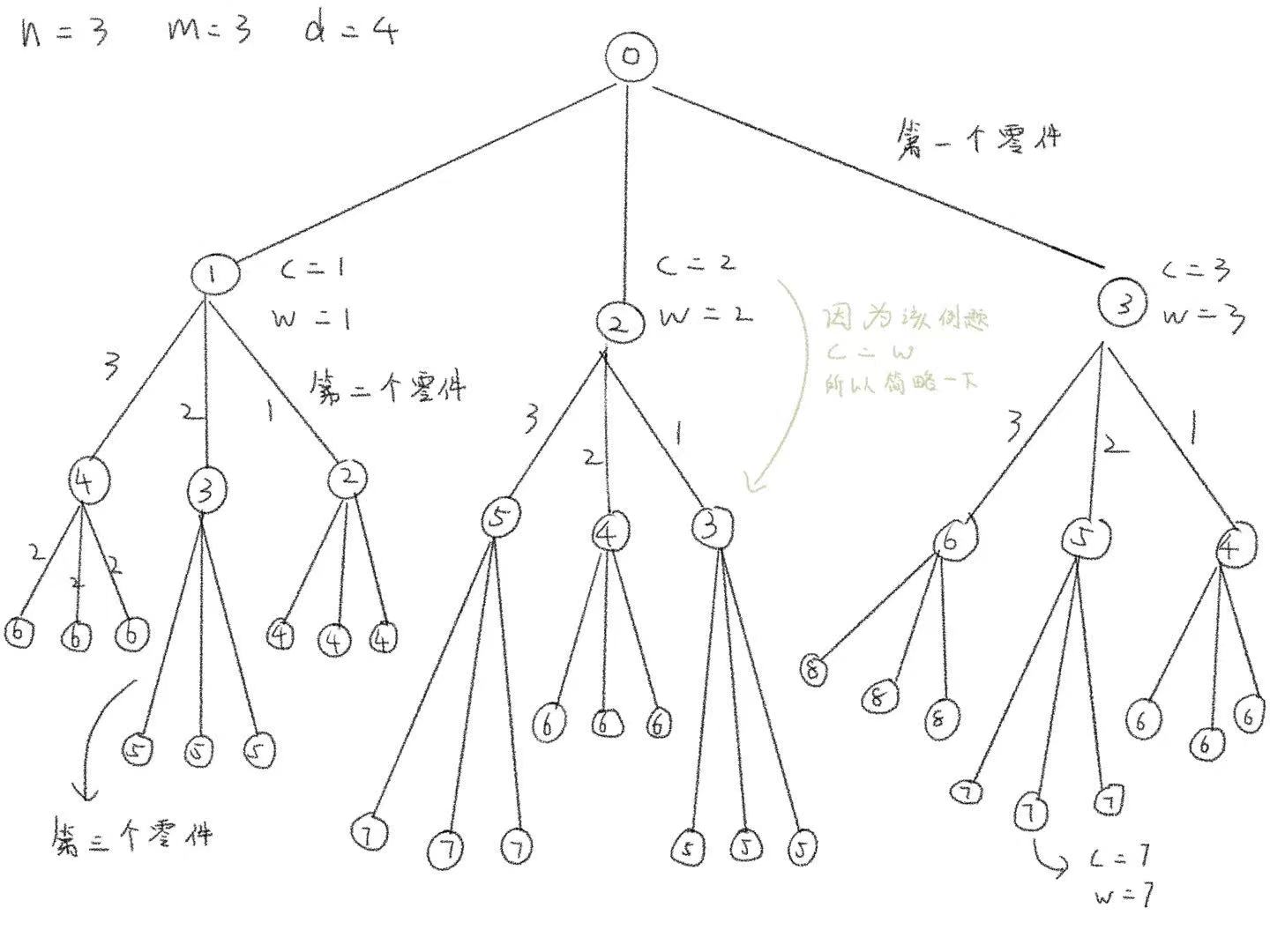
1.3在遍历解空间树的过程中，每个结点的状态值是什么

当前重量nowweight以及当前价格cost。

2.对回溯算法的理解

在使用回溯法解题前需先判断对应的解空间，并可以描绘解空间树以便于对题目的理解

如回溯法名称一样，回溯法需要将当前结点的状态恢复到之前的状态再去更改新的状态

通过将已加的值在改支线已到达叶子节点后回溯到之前的值再走另一支路，从而得到每条支路的结果

当循环到叶子结点时判断每个节点状态，根据比大小来确定是否需要更新min以及对应的数组

同时可以根据题目选择使用剪枝函数减少需要遍历的支路，加快回溯的效率

posted on 2021-12-14 22:01 Russell_0221 阅读(29) 评论(0) 编辑收藏举报

刷新评论刷新页面返回顶部

Russell_0221

导航

公告

算法实践报告第五章

算法实践报告第五章