[读]统计学习方法
这两天看《统计学习方法》，记录了一些知识点。
1.统计学习的方法
从给定的、有限的、用于学习的训练数据集合出发，假设数据时独立同分布产生；并且假设要学习的模型术语某个函数的集合，称为假设空间；应用某个评价准则，从假设空间中选取一个最优的模型，使他对已知训练数据及未知测试数据在给定的评价准则下有最优的预测；最幽默型的选取由算法实现。这样，统计学习方法包括模型的假设空间、模型选择的准则以及模型学习的算法，称其为统计学习方法的三要素，简称为模型、策略和算法。
实现统计学习的步骤如下：
（1）得到一个有限的训练数据集合；
（2）确定包含所有可能的模型的假设空间，即学习模型的集合；
（3）确定模型选择的准则，即学习的策略；
（4）实现求解最优模型的算法，即学习的算法；
（5）通过学习方法选择最优模型；
（6）利用学习的最优模型对新数据进行预测或分析。
2.正则化
模型选择的典型方法是正则化。正则化是结构风险最小化策略的实现，是在经验风险上加一个正则化项或罚项。正则化项一般是模型复杂度的单调递增函数，模型越复杂，正则化值就越大。比如，正则化项可以是模型参数向量的范数。
正则化一般具有如下形式：
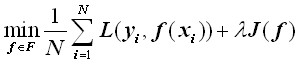
其中，第1项是经验风险，第2项是正则化，λ≥0为调整两者之间关系的系数。
第1项的经验风险较小的模型可能较复杂（有多个非零参数），这时第2项模型复杂度会较大。正则化的作用是选择经验风险与模型复杂度同时较小的模型。
正则化符合奥卡姆剃刀原理，奥卡姆剃刀原理应用于模型选择时变为以下想法：在所有可能选择的模型中，能够很好的解释已知数据并且十分简单才是最好的模型，也就是应该选择的模型。从贝叶斯估计的角度来看，正则化项对应于模型的先验概率，可以假设复杂的模型有较大的先验概率，简单的模型有较小的先验概率。
3.生成模型和判别模型
生成方法由数据学习联合概率分布P(X,Y)，然后求出条件概率分布P(Y|X)作为预测的模型，即生成模型。这样的方法之所以成为生成方法，是因为模型表示了给定输入X产生输出Y的生成关系。典型的生成模型有：朴素贝叶斯和隐马尔科夫模型。
判别方法由数据直接学习决策函数f(X)或者条件概率分布P(Y|X)作为预测的模型，即判别模型。判别方法关心的是对给定输入X，应该预测什么样的输出Y。典型的判别模型包括：k近邻法、感知机、决策树、逻辑回归、最大熵模型、支持向量机、提升方法和条件随机场等。
生成方法的特点：生成方法可以还原出联合概率分布P(X,Y)，而判别方法则不能；生成方法的学习收敛速度更快，即当样本容量增加的时候，学到的模型可以更快地收敛于真实模型；当存在隐变量时，仍可以用生成方法学习，此时判别方法就不能用。
判别方法的特点：判别方法直接学习的是条件概率P(Y|X)或决策函数f(X)，直接面对预测，往往学习的准确率更高；由于直接学习P(Y|X)或f(X)，可以对数据进行各种程度上的抽象、定义特征并使用特征，因此可以简化学习问题。
