关于tarjan的一些感性理解

学长博客-图论

0x0 前论：

在了解完tarjan的基本操作以后，发现这个东西十分的抽象，那么这个时候就需要我们进行一些感性理解以方便记忆。

0x1 关于强连通分量

Part-1 关于强连通

说白了就是一个图上任意两个点都能到达（通俗易懂）

Part-2 关于强连通分量

定义： 极大的强连通子图。

人话： 删一个点这个图就不强连通了，加一个点就成四不像了

0x2 连通性tarjan（不是LCA上的tarjan）

Part-1 关于一个强连通图的“老大”

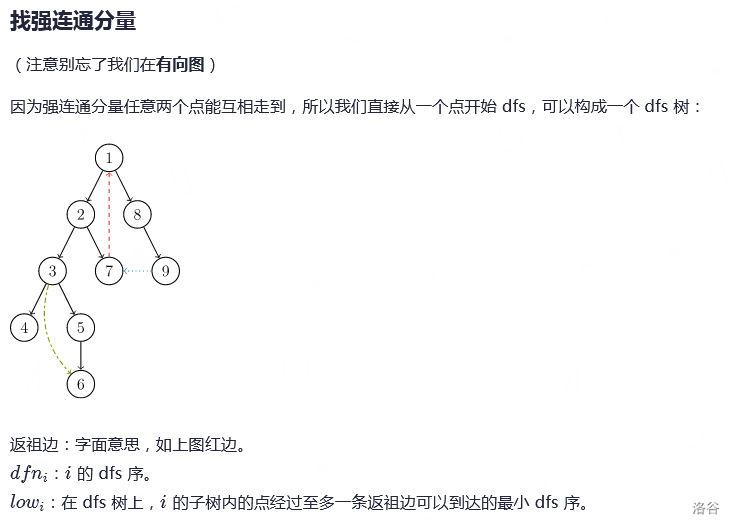
我们给这棵树进行一下形象化解释

这是一个公司的职阶图，其中一个节点的父亲是他的上司，越靠近树的根部职位越高，返祖边就代表着他可以通过某些方式升职或者走关系，从而解决某些以你的职位不能解决的工作和问题。图中的一个强连通分量代表着一个部门，部门与部门之间有从属关系，列如1,2,7就是一个部门，我们给它命名成部门A。

在部门A中，1号是老大（根节点），2号、7号都是他的小弟。2号，7号想要升职，就必须要通过某种方式（返祖边），但是尽管进行了升职，还是没有人能超过1号，最多跟他平起平坐，但是由于一些不可名状的原因（列如辈分，资历，能力等等），他还是老大。

Part-2 关于 dfn 与 low：给员工贴 “身份标签”

上回说到部门 A 里 1 号是老大，2 号、7 号是小弟，返祖边是他们的 “升职路径”。但怎么用算法精准识别 “谁是老大”“谁属于同一个部门”？这就需要给每个员工贴两个关键标签 ——dfn和low，用公司场景把它们扒明白：

dfn [x]：入职编号

想象公司按 “DFS 遍历顺序” 招人，第一个进门的员工给编号 1，第二个给 2，以此类推。这个编号是 “终身制” 的，代表员工加入公司的先后顺序，会出现后加入的人编号在前的情况。比如部门 A 的入职顺序是 1→2→7，那dfn[1]=1、dfn[2]=2、dfn[7]=3；后面部门 B 的 3 号入职编号是 4，4 号是 5，以此类推。

low [x]：部门内 “最早能追溯到的入职编号”

这个标签是员工的 “人脉上限”—— 代表通过 “正常工作汇报”（DFS 树边）或 “跨级走关系”（返祖边），能联系到的公司里最早入职的员工编号。

比如 7 号小弟，通过 “返祖边” 直接找到 1 号老大（入职编号 1），所以他的low[7]会从初始的 3 更新为 1；2 号小弟管理着 7 号，看到下属能联系到 1 号，那他自己的 “人脉上限” 也跟着更新为 1（low[2]=1）；而 1 号老大本身就是部门里最早入职的，没人能比他资历更深，所以low[1]始终等于自己的入职编号 1。

这里的核心逻辑是：同一个部门（强连通分量）的员工，最终的 low 值都会等于 “部门老大” 的 dfn 值。因为不管小弟们怎么 “走关系”“升职”，人脉上限都顶不过老大的资历 —— 老大是部门里最早入职的，也是所有人的人脉终点。

Part-3 栈：待确认的 “部门候选名单”

光有标签还不够，怎么把 “同一部门的人” 凑到一起？Tarjan 算法里的用栈来解决这个问题，其实就是公司的 “部门候选名单”，规则很简单：

员工入职时（DFS 首次访问），直接加入 “候选名单”，标记为 “待分配部门”（对应代码里的zai[x]=1）。
只有等 “老大” 确认后，这份名单才会 “生效”—— 把名单里从栈顶到老大的所有人，正式划为一个部门。

咱们拿部门 A 举例模拟这个过程：

1 号入职，dfn[1]=1、low[1]=1，加入候选名单（栈：[1]）；
1 号的下属 2 号入职，dfn[2]=2、low[2]=2，加入名单（栈：[1,2]）；
2 号的下属 7 号入职，dfn[7]=3、low[7]=3，加入名单（栈：[1,2,7]）；
7 号发现 “返祖边” 能直接联系 1 号，更新low[7]=min(3,dfn[1])=1；
7 号没有更多下属，回溯到 2 号 ——2 号看到下属 7 号的low=1，比自己当前的low=2还小，立刻更新low[2]=1；
2 号没有更多下属，回溯到 1 号 ——1 号检查自己的dfn[1]=1，刚好等于low[1]=1，瞬间明白：“我就是这个部门的老大！”
老大下令：把候选名单里从栈顶到我自己的人，全部划进部门 A！于是弹出 7 号、2 号、1 号（栈清空），给他们贴上 “部门 A” 标签（对应代码里的kuai[x]=ke）。

再看一个跨部门的例子：假设 3 号是部门 B 的老大，入职编号 4（dfn[3]=4），下属 4 号（dfn[4]=5）、5 号（dfn[5]=6），4 号有返祖边到 3 号，5 号有返祖边到 4 号。过程和部门 A 一样：

4 号通过返祖边更新low[4]=4（3 号的 dfn）；
5 号通过 4 号追溯到 3 号，更新low[5]=4；
回溯到 3 号时，dfn[3]=low[3]=4，弹出 5 号、4 号、3 号，组成部门 B。

Part-4 为什么这么设计？—— 老大的 “不可替代性”

可能有人会问：“为什么dfn[x]==low[x]的就是老大？” 用公司场景解释就很直观：

老大是部门里 “资历最深”（dfn 最小）且 “人脉闭环” 的人 —— 小弟们能通过返祖边联系到老大，但老大没法通过任何边联系到比自己资历更深的人（否则他就不是老大了）。所以老大的low值只能等于自己的dfn，这是他的 “身份铁证”。

而小弟们的low值一定会被更新成老大的dfn—— 因为他们能通过 “走关系”（返祖边）或 “下属的关系”（子树之间的传递）联系到老大，人脉上限永远超不过老大。这就保证了：只要找到dfn[x]==low[x]的节点，就能精准锁定部门老大，进而把整个部门的人都 “揪出来”。

Part-5 栈的 “保鲜期”：避免跨部门混淆

为什么要用栈存候选名单？因为公司里的部门是 “层级嵌套” 的，比如部门 A 的老大 1 号，可能同时管理着部门 B 的老大 3 号（相当于 1 号是总监，3 号是部门经理）。

栈的作用就是 “隔离未确认的部门”：在遍历部门 B 的员工时，他们会被加入栈的顶端（此时栈里是 [1,3,4,5]），等 3 号确认老大身份后，只会弹出 3、4、5 组成部门 B，不会影响栈底的 1 号（部门 A 还没确认完）。这种 “先进后出” 的特性，完美适配了 DFS 的嵌套遍历逻辑，避免把不同层级的部门混为一谈。

0x3 总结：

Tarjan 的 “部门划分” 三步法

用公司场景总结 Tarjan 找强连通分量的核心逻辑，记住这三步就够了：

1，贴标签：给每个员工分配 “入职编号”（dfn）和 “人脉上限”（low）；

2，入名单：员工入职时加入 “候选名单”（栈），等待部门分配；

3，找老大：回溯时检查是否有人脉上限等于自己入职编号的员工（老大），找到后把名单里的人划成一个部门。

本质上，Tarjan 算法就是通过 “追溯资历”（low 数组）和 “锁定核心”（dfn==low），把公司里 “能互相走关系、形成闭环” 的员工们，精准划分成一个个独立的部门（强连通分量）。而这些部门最终会构成一个层级分明的 “公司架构图”（DAG），这也是后续缩点、拓扑排序的基础。