子串周期查询

大概就是复读集训队论文，大部分证明都略去了。

前置知识

• WPL: \(s\) 有 period \(p_1 + p_2 \le n \implies\) \(s\) 有 period \(\gcd(p_1, p_2)\)
• \(s\) 的长 \([l, 2l)\) borders 构成一段等差数列
• \(s\) 的 borders 构成 \(\log |s|\) 段等差数列
• \(2 |s| \ge |t| \implies s\) 在 \(t\) 中出现的位置构成等差数列，且公差为 \(s\) 的最小周期（证明：反证，直接考虑 \(s\) 出现的位置覆盖的段，应用 WPL 即可）

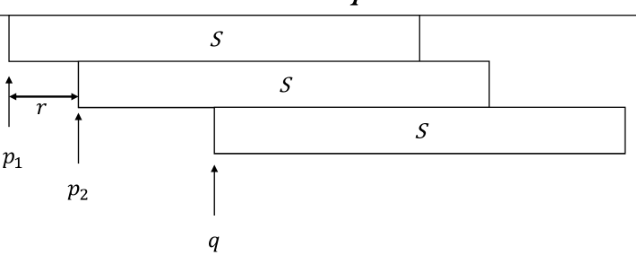
算法流程

首先可以把一个 border \(b, k = \lfloor \log |b| \rfloor\) 分解成前 \(2^k\) 和后 \(2^k\)（类似 ST 表），分别比较即可。

现在考虑求出长度 \([2^k, 2^{k+1})\) 的 borders。

那么把原串的 \(2^k\) 前缀和 \(2^{k+1}\) 后缀匹配，\(2^k\) 后缀和 \(2^{k+1}\) 前缀匹配（匹配位置都是等差数列），将等差数列求交即可。

处理这个需要将所有长为 \(2^k\) 的子串排序，直接用倍增法即可 \(\mathcal O(n \log n)\)。

如果二分求出这段等差数列就可以得到 \(\mathcal O(\log^2 n)\) 的查询。

考虑我们是要求一个子串 \(t\) 所有匹配位置和一段 \(2^k + 1\) 个数的区间求交，那么将串按 \(2^k\) 分块，一个求交的区间会恰好落在两个块里，那么我们处理出三元组 \((t, b, P)\) 表示长 \(2^k\) 子串 \(t\) 在 \(b\) 块中匹配位置为等差数列 \(P\)。这样的组数不超过处理的子串总数，即 \(\mathcal O(n \log n)\)（没有匹配任何位置则不存），那么用字符串双 hash 和 hash 表即可 \(\mathcal O(1)\) 查询。最后通过讨论将两个块中查询出的信息合并为一个等差数列。

然后考虑对两个等差数列求交。发现我们要求交的等差数列形如这样：\(|x_1| = |x_2| = |y_1| = |y_2| = 2^k\)，\(x_1\) 在 \(y_1y_2\) 中的匹配位置和 \(y_2\) 在 \(x_1x_2\) 中的匹配位置，如果都匹配了至少 \(3\) 次，那么公差必然一样。

下面证明：

首先根据前置知识最后一条，设 \(r_1, r_2\) 分别为 \(x_1, x_2\) 最小周期，\(r_2 < r_1\)。

画出匹配图，可以得出 \(x_1\) 的长度至少为 \(2r_1\) 的后缀有周期 \(r_2\)（通过观察 \(x_1\) 的后缀匹配了 \(x_2\) 的一个前缀）。使用 WPL 立即得到 \(x_1\) 长度至少 \(2r_1\) 的后缀有周期 \(\gcd(r_1, r_2)\)，故 \(x_1\) 的 \(r_1\)-period 有整周期，与 \(r_1\) 是最小周期矛盾。

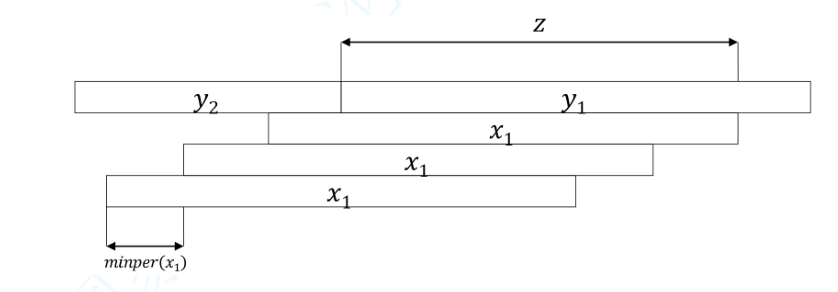
（符号不太一样）

那么通过一些讨论也可以 \(\mathcal O(1)\) 合并等差数列。通过枚举 \(k\) 就可以得到 \(\mathcal O(\log n)\) 的算法。

下面是 P4482 [BJWC2018]Border 的四种求法 的代码（求最长 border）

最好手写固定大小 hash 表（unordered_map 在 \(5 \times 10^6\) 次级别的查询都可能耗费很长的时间），否则很可能跑不过 SAM 暴力 \(\mathcal O(\log^2 n)\)。原题数据不强，代码仅供参考。

#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
#include <ctime>
#include <numeric>
#include <vector>
#include <cassert>
#include <unordered_map>
using namespace std;

#define LOG(f...) fprintf(stderr, f)
// #define DBG(f...) printf(f)
#define DBG(f...) void()
#define all(cont) begin(cont), end(cont)
#ifdef __linux__
#define getchar getchar_unlocked
#define putchar putchar_unlocked
#endif

using ll = long long;
using ull = unsigned long long;

template <class T> void read(T &x) {
  char ch; x = 0;
  int f = 1;
  while (isspace(ch = getchar()));
  if (ch == '-') ch = getchar(), f = -1;
  do x = x * 10 + (ch - '0'); while(isdigit(ch = getchar()));
  x *= f;
}
template <class T, class ...A> void read(T &x, A&... args) { read(x); read(args...); }

const int N = 200005;
const int M = 0x7FFFFFFF;
const ull MAGIC = 0x21b699768c4aed5f;
const int B1 = 131, B2 = 248;
int cnt = 0;

// arithmetic progression
struct ap {
  int s, t, d;
};
const ap EMPTY = {1, 0, 0};
bool contains(const ap &a, int x) {
  if (a.s > a.t) return false;
  if (!a.d) return x == a.s || x == a.t;
  return a.s <= x && x <= a.t && (x - a.s) % a.d == 0;
}

char s[N];
int n;
int h1[N], h2[N], np1[N], np2[N];

void init_hash() {
  np1[0] = np2[0] = M - 1;
  for (int i = 0; i < n; ++i) {
    np1[i + 1] = (ll)np1[i] * B1 % M;
    np2[i + 1] = (ll)np2[i] * B2 % M;
  }
  for (int i = 0; i < n; ++i) {
    h1[i + 1] = ((ll)B1 * h1[i] + s[i]) % M;
    h2[i + 1] = ((ll)B2 * h2[i] + s[i]) % M;
  }
}
ull range(int l, int r) {
  return ull((h1[r] + (ull)h1[l] * np1[r - l]) % M) << 32 | ull((h2[r] + (ull)h2[l] * np2[r - l]) % M);
}

struct hasher {
  ull operator()(const pair<ull, int> &p) const { return p.first + p.second * MAGIC; }
};

struct hashtable {
  static const int MASK = (1 << 22) - 1;
  struct node {
    ull k;
    ap v;
    node *nxt;
  } v[N * 18];
  node *hd[MASK + 1], *alloc = v;

  void emplace(ull p, ap v) { *alloc = {p, v, hd[p & MASK]}; hd[p & MASK] = alloc++; }
  node *find(ull p) { node *n = hd[p & MASK]; while (n && n->k != p) n = n->nxt; return n; }
} dict;

// unordered_map<pair<ull, int>, ap, hasher> dict;
int maxw;

namespace internal {
  int sa[N], rk[N], sec[N], m;
  int pos[N];

  void radix_sort(int n) {
    memset(pos, 0, sizeof(pos));
    for (int i = 0; i < n; ++i)
      ++pos[rk[i]];
    partial_sum(pos, pos + m, pos);
    for (int i = n - 1; i >= 0; --i)
      sa[--pos[rk[sec[i]]]] = sec[i];
  }

  void build() {
    // dict.reserve(n * 40);
    for (int i = 0; i < n; ++i)
      rk[i] = s[i] - 'a', sec[i] = i;
    m = 26;
    radix_sort(n);

    for (int w = 2; w < n; w <<= 1) {
      int p = 0, l = w >> 1, cnt = n - w + 1;
      int bw = __lg(w);
      for (int i = 0; i < n; ++i)
        if (sa[i] + l <= n && sa[i] >= l)
          sec[p++] = sa[i] - l;
      radix_sort(cnt);
      memcpy(sec, rk, sizeof(rk));
      rk[sa[0]] = 0;
      for (int i = 1; i < cnt; ++i)
        rk[sa[i]] = rk[sa[i - 1]] + (sec[sa[i]] != sec[sa[i - 1]] || sec[sa[i] + l] != sec[sa[i - 1] + l]);
      m = rk[sa[cnt - 1]] + 1;
      if (m == cnt) break;
      maxw = bw;

      for (int l = 0, r; l < cnt; l = r) {
        r = l;
        while (r != cnt && rk[sa[r]] == rk[sa[l]]) ++r;
        ull hsh = range(sa[l], sa[l] + w);
        int last = -1;
        ap prog;
        for (int i = l; i < r; ++i) {
          if (sa[i] >> bw != last) {
            if (~last) {
              // dict.insert({make_pair(hsh, last), prog});
              dict.emplace(hsh + last * MAGIC, prog);
            }
            prog = {sa[i], sa[i], 0};
            last = sa[i] >> bw;
          }
          else {
            prog.d = sa[i] - sa[i - 1];
            prog.t = sa[i];
          }
        }
        dict.emplace(hsh + last * MAGIC, prog);
        // dict.insert({make_pair(hsh, last), prog});
      }
    }
  }
}

ap _reduce(ap a, int l, int r) {
  if (a.s > a.t) return a;
  if (a.s + a.d == a.t) {
    if (l <= a.s && a.t < r) return a;
    if (l <= a.s && a.s < r) return {a.s, a.s, 0};
    if (l <= a.t && a.t < r) return {a.t, a.t, 0};
    return EMPTY;
  }
  if (a.s < l) a.s += (l - a.s + a.d - 1) / a.d * a.d;
  if (a.t >= r) a.t -= (a.t - r + a.d) / a.d * a.d;
  return a;
}
ap occurence(int l, int r, int pl, int pr, int bs) {
  ull hsh = range(l, r);
  int bl = pl >> bs;
  auto it1 = dict.find(hsh + bl * MAGIC), it2 = dict.find(hsh + (bl + 1) * MAGIC);
  ap a = it1 ? it1->v : EMPTY;
  ap b = it2 ? it2->v : EMPTY; 
  // auto it1 = dict.find(make_pair(hsh, bl)), it2 = dict.find(make_pair(hsh, bl + 1));
  // ap a = it1 == dict.end() ? EMPTY : it1->second;
  // ap b = it2 == dict.end() ? EMPTY : it2->second;
  ++cnt;
  a = _reduce(a, pl, pr); b = _reduce(b, pl, pr);
  if (a.s > a.t) return b;
  if (b.s > b.t) return a;
  return {a.s, b.t, b.s - a.t};
}

int query(int l, int r) {
  if (l == r) return 0;
  int k = __lg(r - l);
  for (int i = min(k, maxw); i; --i) {
    int lb = 1 << i, rb = min(1 << (i + 1), r - l - 1);
    ap a = occurence(l, l + lb, r - rb, r - lb + 1, i);
    ap b = occurence(r - lb, r, l, l + lb + 1, i);
    if (a.s > a.t || b.s > b.t) continue;
    tie(a.s, a.t) = make_pair(l + r - a.t - lb, l + r - a.s - lb);
    if (b.s + b.d == b.t) swap(a, b);
    int max_inter = -1;
    if (a.s + a.d == a.t) {
      if (contains(b, a.t)) max_inter = a.t;
      else if (contains(b, a.s)) max_inter = a.s;
    }
    else {
      if ((b.s - a.s) % b.d != 0) continue;
      int l = max(a.s, b.s), r = min(a.t, b.t);
      if (l <= r) max_inter = r;
    }
    if (~max_inter)
      return max_inter - l + lb;
  }
  return l + 1 != r && s[l] == s[r - 1];
}

int main() {
#ifdef LOCAL
  freopen("input.txt", "r", stdin);
  freopen("output.txt", "w", stdout);
#endif
  scanf("%s", s);
  n = strlen(s);
  init_hash();
  internal::build();
  int qc;
  read(qc);
  while (qc--) {
    int l, r;
    read(l, r);
    --l;
    printf("%d\n", query(l, r));
  }
  LOG("hashes : %d\n", cnt);
  return 0;
}