差分约束基本讲解
如果一个系统由 n 个变量和 m 个约束条件组成，每个约束条件形如 \(x_j-x_i<=b_k\)，其中 \(i,j\in[1,n],k\in[1,m]\)，则称其为差分约束系统（System of Difference Constraints）。亦即，差分约束系统是求解关于特殊的 \(N\) 元一次不等式组的方法。
我们先来看一个简单的数学问题，如下给定 4 个变量和 5 个不等式约束条件，求 \(x_3-x_0\) 的最大值。
我们可以通过不等式的两两加得到三个结果，
由以上结果很容易得知，\(x_3-x_0\) 的最大值是 7，也就是上面三式里的最小值。
这个例子很简单，只有 4 个变量和 5 个不等式约束条件，那如果有上百变量上千约束条件呢？仅凭肉眼手工计算效率太差，因此我们需要一个较为系统的解决办法。
我们先来看一幅图，如下，给定四个小岛以及小岛之间的有向距离，问从 0 号岛到 3 号岛的最短距离。箭头指向的线代表两个小岛之间的有向边，蓝色数字代表距离权值。
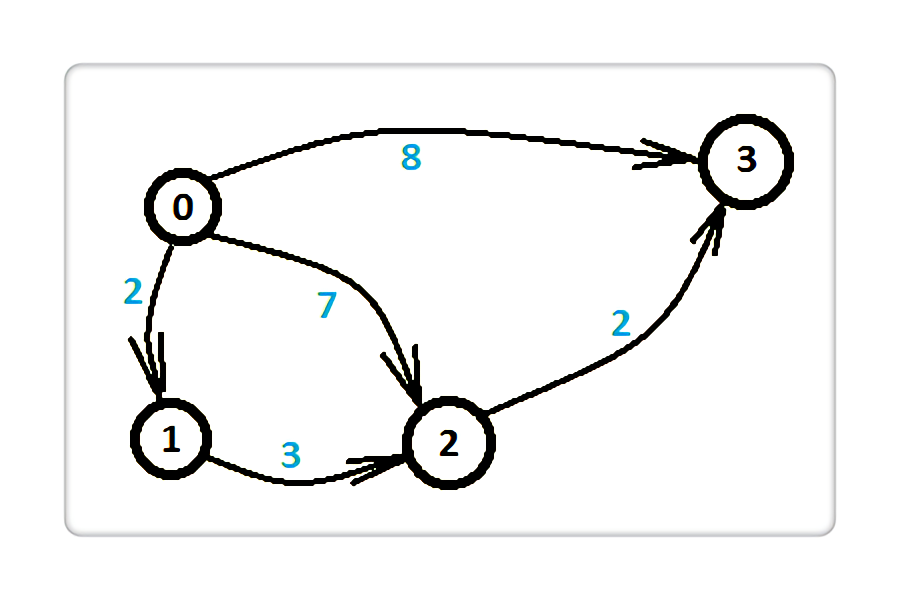
这个问题就是经典的最短路问题。由于这个图比较简单，我们可以枚举所有的路线，发现总共三条路线，如下：
-
0 -> 3，长度为 8
-
0 -> 2 -> 3，长度为 7 + 2 = 9
-
0 -> 1 -> 2 -> 3，长度为 2 + 3 + 2 = 7
最短路为三条线路中的长度的最小值，即 7，所以最短路的长度就是 7。细心的读者会发现，这幅图和最上方的五个不等式约束条件是有所关联的，但这个关联并不是巧合，而正是我们接下来要讲的那个 "系统的解决办法"。
差分约束与最短路
差分约束系统中的每个约束条件 \(x_i-x_j<=c_k\) 都可以变形成 \(x_i<=x_j+c_k\)，这与单源最短路中的三角形不等式 \(dist[y]<=dist[x]+z\) 非常相似。
因此，我们可以把每个变量 \(x_i\) 看做图中的一个结点，对于每个约束条件 \(x_i-x_j<=c_k\)，看成是从结点 \(j\) 向结点 \(i\) 的一条权值为 \(c_k\) 的有向边，于是我们就可以把一个差分约束系统转化成图的最短路问题。
然而在实际问题中情况往往会复杂得多，例如，把条件约束里的所有等号去掉，
这个时候我们就需要将上面的小于号转换成小于等于号。
当 \(x_i\) 被限定只能是整数时，这个转换就会非常简单，
总结
差分约束问题下，
- 如果要求最大值，则想办法把每个不等式变为标准 \(x_i-x_j<=c_k\) 的形式，然后建立一条从 \(j\) 到 \(i\) 权值为 \(c_k\) 的边，最后求最短路径即可。
- 如果要求最小值，则想办法把每个不等式变为标准 \(x_i-x_j>=c_k\) 的形式，然后建立一条从 \(j\) 到 \(i\) 权值为 \(c_k\) 的边，最后求最长路径即可。
基本题
CodeVS 4416 - FFF 团卧底的后宫
给出 n 个形如 $x_i - x_j <= d $ 或 $x_i - x_j >= d $ 的不等式，求一组使 $x_1 $ 与 \(x_n\) 差最大的解，输出最大差值，若无解输出 -1，若 \(x_1\)与 \(x_n\) 的差为无限大则输出 -2。
#include <cstdio>
#include <climits>
#include <algorithm>
#include <queue>
const int MAXN = 1000;
const int MAXM = 10000;
struct Edge;
struct Node;
struct Node {
Edge *edges;
bool inQueue;
int dist;
int count;
} nodes[MAXN];
struct Edge {
Node *from, *to;
int w;
Edge *next;
Edge(Node *from, Node *to, int w) : from(from), to(to), w(w), next(from->edges) {}
};
int n, m, k;
inline void addEdge(int from, int to, int w) {
nodes[from].edges = new Edge(&nodes[from], &nodes[to], w);
}
inline bool bellmanFord() {
std::queue<Node *> q;
q.push(&nodes[0]);
while (!q.empty()) {
Node *node = q.front();
q.pop();
node->inQueue = false;
for (Edge *edge = node->edges; edge; edge = edge->next) {
if (edge->to->dist > node->dist + edge->w) {
edge->to->dist = node->dist + edge->w;
if (!edge->to->inQueue) {
edge->to->inQueue = true;
edge->to->count++;
q.push(edge->to);
if (edge->to->count > n) {
return false;
}
}
}
}
}
return true;
}
int main() {
scanf("%d %d %d", &n, &m, &k);
for (int i = 0; i < n; i++) {
nodes[i].dist = INT_MAX;
}
nodes[0].dist = 0;
for (int i = 0; i < m; i++) {
int a, b, d;
scanf("%d %d %d", &a, &b, &d);
a--, b--;
addEdge(a, b, d);
// $b - $a <= d
// $a + d >= $b
}
for (int i = 0; i < k; i++) {
int a, b, d;
scanf("%d %d %d", &a, &b, &d);
a--, b--;
addEdge(b, a, -d);
// b - a >= d
// a - b <= -d
// b + -d >= a
}
if (!bellmanFord()) {
puts("-1");
} else {
if (nodes[n - 1].dist == INT_MAX) {
puts("-2");
} else {
printf("%d\n", nodes[n - 1].dist);
}
}
return 0;
}
