P12911 [POI 2020/2021 R2] 棋盘 / Projekt planszy

有趣的构造题。

看了两位金钩大神写的进制拆分，颇受启发。

在此提供一种有点暴力但是简单易懂、具有普遍性的构造方案。

---

题目要求 \(1 \leq n \leq 100\)，我们直接将网格开到 \(100 \times 100\)。

定义 \(a_{i,j}\) 表示格子 \((i,j)\) 的状态，当 \(a_{i,j}=1\) 时 \((i,j)\) 被封锁，否则未被封锁。

初始时除起点与终点外的所有格子均被封锁。

---

考虑将 \(K\) 条路径拆分。设 \(K\)（\(K \leq 10^{18}\)）的第 \(i\) 个数位（定义个位为第 \(0\) 位）的数值为 \(w_i\)，则：

\[K = \sum\limits_{i=0}^{18}(w_i \times 10^i). \]

例如，\(1949 = 0 \times 10^{18} + \cdots + 0 \times 10^4 + 1 \times 10^3 + 9 \times 10^2 + 4 \times 10^1 + 9 \times 10^0\)。

---

定义『块』为 \(3 \times 4\) 的网格。

一个从左上角走至右下角有 \(n\) 条合法路径的『块』被称为『\(n\) 类块』。

下面给出『\(0\) 类块』至『\(10\) 类块』的一种构造方案。

#...  ....  ....  ...#  ....  ...#  ....  ....  ...#  ....  ....
....  ###.  .##.  #..#  .#..  #...  #...  ....  ....  ....  ....
....  ###.  ....  #...  ....  #...  #...  ##..  #...  #...  ....

容易证明，将一个『\(n\) 类块』的右下角与一个『\(m\) 类块』的左上角连接后，从『\(n\) 类块』的左上角走至『\(m\) 类块』的右下角的合法方案数为 \(n \times m\)。

---

开始构造。我们在图的顶部放置 \(19\) 个『块』（红色），其中第 \(i\) 个『块』为『\(w_i\) 类块』。（\(i \in [0,18]\)，设最右边的为第 \(0\) 个『块』，即 \(K\) 的个位所对应的『块』）

在底下放置 \(18\) 个『\(10\) 类块』（蓝色）。

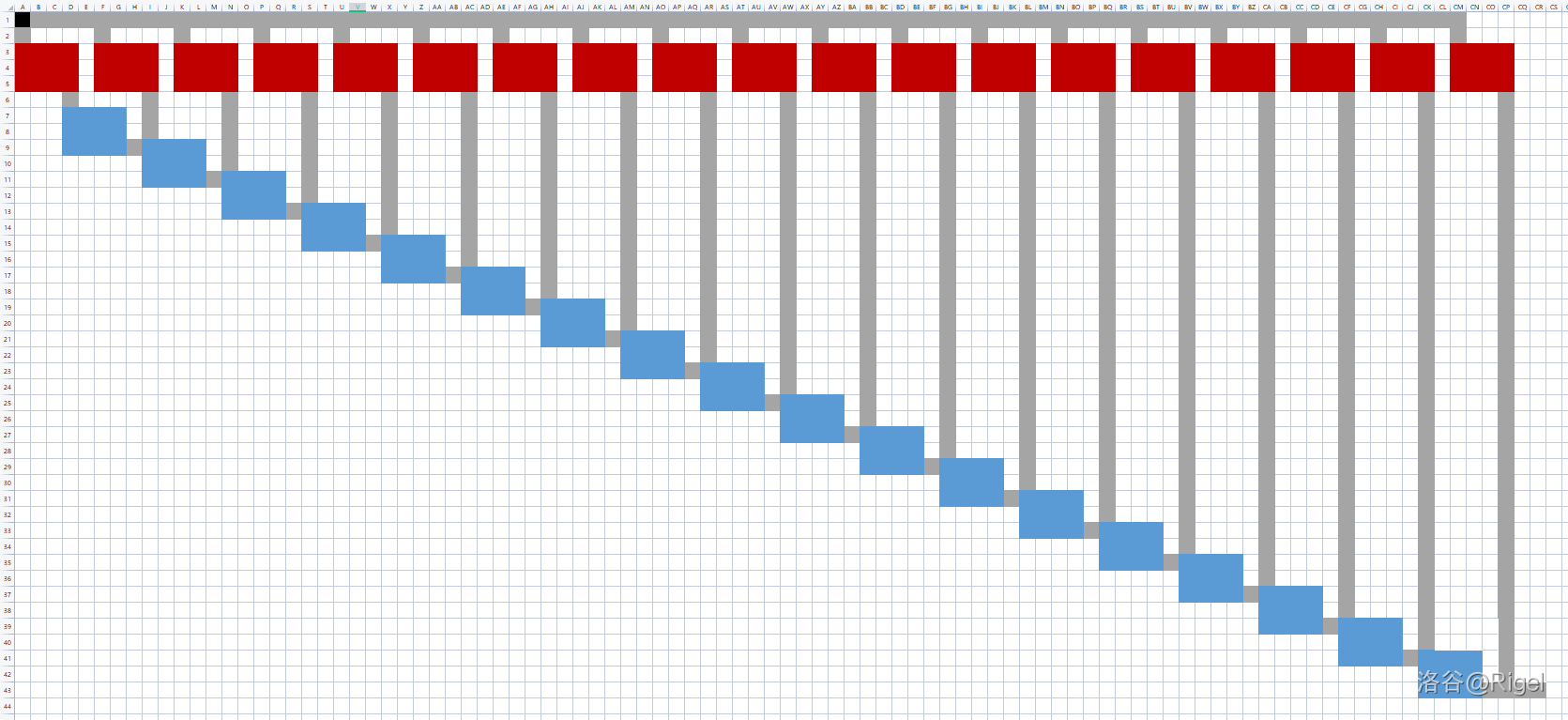
将这些『块』按上图方式连接。

从起点开始走，经过上面的第 \(i\) 个『块』之后，还会经过 \(i\) 个『\(10\) 类块』，因此走到右下角的合法路径数为 \(w_i \times 10^i\)。

整个结构的合法路径数为每种走法的合法路径数之和，也就是 \(\sum\limits_{i=0}^{18}(w_i \times 10^i) = K\)。

结构的长度（横向）为 \(18 \times 2 + 7 = 43\)，宽度（纵向）为 \(18 \times 5 + 4 = 94\)，符合题目要求。

最后将结构的右下角连接至终点即可。

---

Submission。