P5088 矩形

思路

将原图逆时针旋转 \(90 \degree\) 并建系。

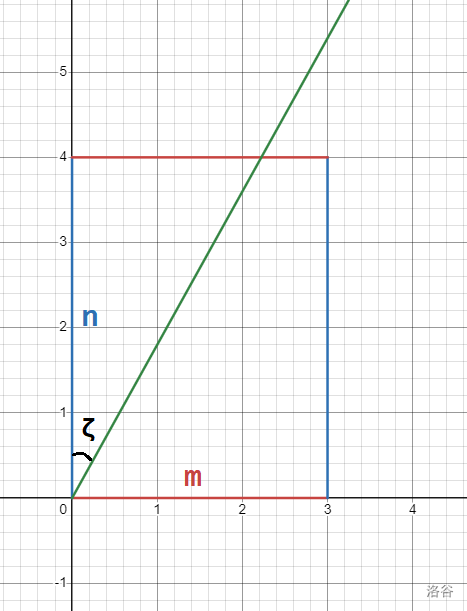
考虑到直接模拟光路较为复杂，我们可以建立如图所示的镜像单元格。

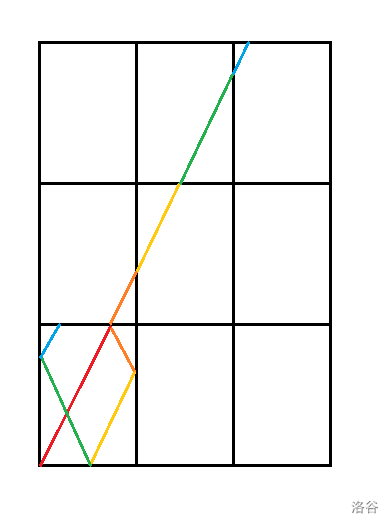
容易证明，图中同色线段长度相等。

于是问题就转换为：求直线第一次到达形如 \((k_1m,k_2n)\) 的点（其中 \(k_1,k_2 \in \mathbb N_+\)）途中穿过矩形边的次数。

由于 \(\cot \zeta = \displaystyle{\frac{a}{b}}\)，因此直线的解析式为 \(y = \displaystyle{\frac{a}{b}} \cdot x\)。

设直线第一次到达的点为 \((k_1m,k_2n)\)，则：

\( \begin{aligned} \displaystyle{\frac{a}{b}} \cdot k_1m&=k_2n\\ amk_1&=bnk_2\\ k_1&=\displaystyle{\frac{bnk_2}{am}}. \end{aligned} \)

由于 \(k_1 \in \mathbb N_+\)，故 \(am \mid bnk_2\)。

容易证明，\(k_2\) 的最小值为 \(\displaystyle{\frac{am}{\gcd(am,bn)}}\)，此时 \(k_1=\displaystyle{\frac{bn}{\gcd(am,bn)}}\)。

我们回到 \(k_1\) 与 \(k_2\) 的定义，不难得出最终答案为 \(k_1+k_2-2\)。

---

注意以下两点：

• 在开始时要先化简。令 \(g_1 = \gcd(n,m)\)，\(g_2 = \gcd (a,b)\)，并使 \(n \gets \displaystyle{\frac{n}{g_1}}\)，\(m \gets \displaystyle{\frac{m}{g_1}}\)，\(a \gets \displaystyle{\frac{a}{g_2}}\)，\(b \gets \displaystyle{\frac{b}{g_2}}\)。

• 特判 \(a=0\) 或 \(b=0\) 的情况。

代码

#include<bits/stdc++.h>
#define int long long

using namespace std;

int n,m,a,b;

inline int read(){
	int ret=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9')ret=ret*10+(ch&15),ch=getchar();
	return ret*f;
}

int gcd(int x,int y){
	return y?gcd(y,x%y):x;
}

int solve(int n,int m,int a,int b){
	if(!a||!b)return 0;
	int g1=gcd(n,m),g2=gcd(a,b);
	n/=g1,m/=g1,a/=g2,b/=g2;
	int g=gcd(a*m,b*n);
	int k1=b*n/g,k2=a*m/g;
	return k1+k2-2;
}

signed main(){
	n=read(),m=read(),a=read(),b=read();
	printf("%lld\n",solve(n,m,a,b));
	return 0;
}