例题引入：维护一个序列 \(a\)，支持单点加操作，查询区间和。
(我不会告诉你学完线段树后树状数组就没用了)

1.简化版本

0x01.无操作，查询单点值

就是一个最朴素的数组，入门语法题

0x02.单点加，查询单点值

还是语法题，没手都行

0x03.无操作，查询区间和

红题，前缀和，设。
\(s_k=\sum_{i=1}^{k} a_i\)
答案即为 \(s_r-s_{l-1}\)。

2.暴力

最基础的暴力就是每次查询从 \(l\) 到 \(r\) 挨个加起来，这样每次查询就是 \(O(n)\) 的。

于是还是引进前缀和。
我们发现，如果修改第 \(i\) 个数，那么 \(s_1,s_2,\dots,s_{i-1}\),的值都不会发生改变。
而 \(s_i,s_{i+1},\dots,s_n\) 的值则被修改。
于是现在查询变为了 \(O(1)\)，而修改变为 \(O(n)\) 的了。

我们想让查询和修改“中和一下”，都是 \(O(\log n)\)。

3.lowbit

在引入树状数组之前，我们需要先学习这个重要的概念： lowbit。
一个数 \(x\) 的 lowbit 被定义为，\(x\) 在二进制下为 \(1\) 的最低位。
例如 \(28=(11100)_2\) ，第一位，第二位都是 \(0\)，第三位是 \(1\)，所以第三位就是它的 lowbit，而二进制下的第三位是 \(4\)，所以 \(28\) 的 lowbit 是 \(4\) 。以此类推， \(9\) 的 lowbit 是 \(1\) ， \(32\) 的 lowbit 是 \(32\) ……

如何计算 lowbit ?
最朴素的方法就是将这个数转换成二进制，再从低位到高位一位一位地判断，复杂度 \(O(\log n)\)。
但是这样又慢，代码又长。所以我们需要一些没用的 CSP 第一轮的知识——二进制补码。
众所周知，在二进制下 \(-x\) 会被转化为 \(\sim x+1\) （也就是 \(x\) 的每一位取反得到 \(\sim x\) 然后再对 \(\sim x\) 加 \(1\) 。
举个例子：\(28=(11100)_2\)，\(-28=(00100)_2\)。
那么，每个数 \(n\) 的二进制其实都是:

\(*****100......0\)

前面的 "*" 是无关紧要的位，当然最后的“ \(0\) ”的数量也有可能是 \(0\)。
于是 \(-n\) 的二进制就是：
\(*****011......1 + 1 = *****100......0\)

现在计算 \(n\&(-n)\) ,“\(\&\)”是按位与。
前面的星号位都取反了，所以按位与的值都是 \(0\)。
这是很显然的。
而后面若干个 \(0\) 与完之后仍然是 \(0\)。
故 \(n\&(-n)\) 的二进制就是：

\(00......0100......0\)

而这个唯一的“\(1\)”，就是原先的 \(n\) 最低的一位 \(1\) ，也就是 \(\text{lowbit}(n)\)！
所以得出 \(\text{lowbit}(n) = n\&(-n)\)。
前面的推导不懂也没关系，把这个公式记住就行。

4.单点修改

定义 \(c_i\) 为在a数组中，以i为末尾，长度为 lowbit(i) 的区间和。
形式化的说，\(c_i\) "管辖"了这段区间
比如说：
\(c_1 =a_1\)
\(c_2 = a_1+ a_2\)
\(c_3= a_3\)
\(c_4= a_1 + a_2 + a_3 + a_4\)
\(c_5=a_5\)
\(c_6=a_5+a_6\)
\(c_7=a_7\)
\(c_8= a_1 + a_2 + a_3 + a_4 +a_5+a_6+a_7+a_8\)
\(c_9=a_9\)
\(c_{10}=a_9+a_{10}\)
\(c_{11}=a_{11}\)
\(c_{12}=a_9+a_{10}+a_{11}+a_{12}\)
......

再放一个清朝老图：

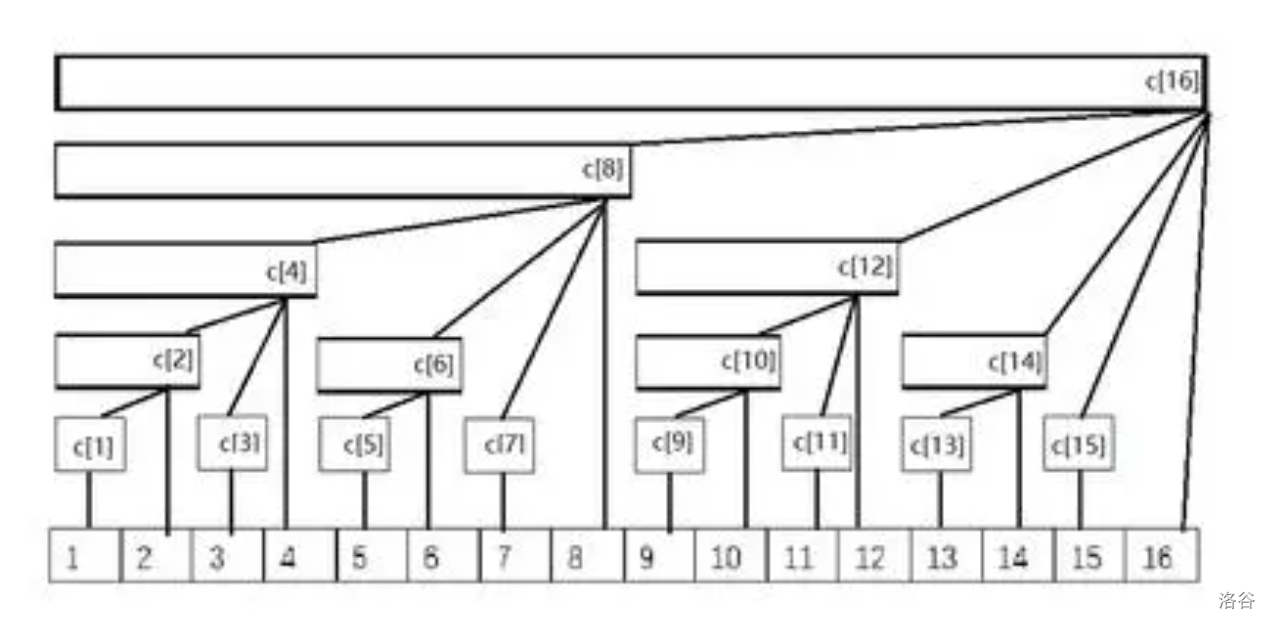
此时比如说我要将 \(a_5\) 加上 \(1\)，那么 \(c_5,c_6,c_8,c_{16}\) 都需要加 \(1\)。
那么如何知道修改一个 \(a_i\) 后会有哪些 \(c\) 数组的值发生改变呢？
看回这个图，发现 \(c\) 数组构成了一棵树，这也就是“树状数组”名字的由来，这棵树的叶子节点是 \(a_i\)，而修改一个 \(a_i\)，从它自己到树根这条路径上的所有点值都会发生修改。
所以问题就转化为如何求 \(c_i\) 的父亲节点。
观察图可得 \(c_i\) 的父亲节点是 \(c_{i+\text{lowbit}(i)}\) 。具体为什么我不会证。
所以就好了，每次修改 \(a_i\) 时，从 \(c_i\) 开始，一直跳父亲直到跳到根为止，跳的过程中把每个点的值修改即可。

void add(int x,int y){
	for(int i=x;i<=n;i+=lowbit(i)) c_i += y;
}

\(x\) 是要修改的位置的下标，\(y\) 是 \(a_{x}\) 要加上的值。

5.查询区间和

其实相当于查询前缀和……
譬如说，要查询 \(a_1\) + \(a_2\) +......+ \(a_{11}\)。
首先从 \(c_{11}\) 开始，发现 \(c_{11} = a_{11}\)，于是 \(ans \gets ans+c_{11}\)。
然后跳到 \(c_{10}\)，发现 \(c_{10} = a_9 + a_{10}\) ,于是 \(ans \gets ans+c_{10}\)。
然后跳到 \(c_8\)，发现 \(c_8 = a_1 +...+ a_8\) ,于是 \(ans \gets ans+c_8\)。
此时， \(a_1\) 到 \(a_{11}\) 所有的值都被加到 \(ans\) 里面了,
结束。

注意到每次从 \(c_i\) 跳到 \(c_{i-\text{lowbit}(i)}\) ,一直跳到 \(0\)。

int ask(int x){//查询a_1+a_2+......+a[n];
	int ans=0;
	for(int i=x;i;i-=lowbit(i)) ans+=c_i;
	return ans;
}

最后如果要查询 \(a_{l}+a_{l+1}+\dots+a_{r-1}+a_{r}\) ,那么就输出 \(\text{ask}(r)-\text{ask}(l-1)\) 即可。

同理，树状数组可以处理区间积，区间异或和等。
它们需要保证有逆运算，即 “可差分”，这样才能用前缀和思想处理。
所以树状数组一般不能处理区间最值等问题。

最后，显然每次修改或查询的复杂度是 \(\Theta(logn)\)。

6.区间加，单点查询

用树状数组维护 \(a\) 数组的差分数组。
这样区间修改就变为了差分数组的两个单点修改，单点查询就变成了差分数组的区间查询（原数组是差分数组的前缀和）。

7.其他

I.区间加，区间查询

详见此处
说实话这玩意没有用，线段树比这简洁多了。
但是这令我想起曾经见过一位大佬用一个奇怪的花式树状数组实现了主席树的功能！
（话说直接学主席树不好吗）……

II.权值树状数组

不如权值线段树，等到讲到主席树时再说吧……