线段树

例题引入:维护一个序列 \(a\),支持区间加,查询区间和
1.结构
线段树是一棵二叉树,树根的“管辖范围”是 \(a[1]\) 到 \(a[n]\)。
每个节点的左儿子的管辖范围是该节点管辖范围的左半段,
右儿子的管辖范围是该节点管辖范围的右半段。
叶子节点的管辖范围就是 \(a[i]\)。
如图所示:(OI-wiki的图太丑了,网上找了个清晰点的)
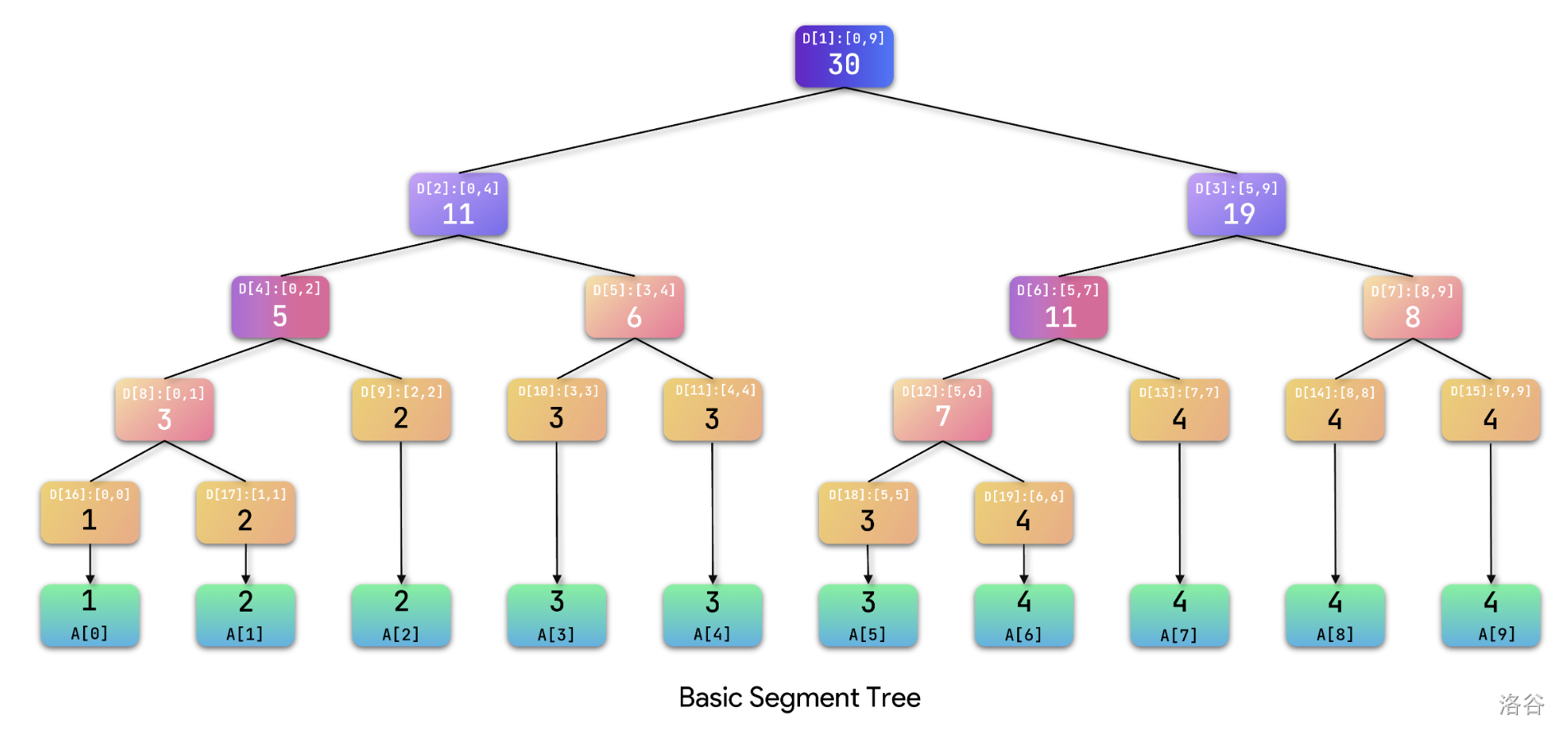
其中每个节点上的小字是它的管辖范围,大字则是其管辖范围的区间和。
2.建树
考虑递归地建立一棵线段树。
首先建立 \(1\) 号节点,它的管辖范围是 \([1,n]\)。
然后对于每一个节点 \(i\),它的左儿子编号为 \(2i\) ,右儿子编号为 \(2i+1\)。
建立以 \(i\) 号节点为根的子树时,就先建立其左子树,再建立其右子树,最后合并左右子树所维护的信息即可。
递归的终止条件是如果 \(i\) 号节点的管辖区间为 \([l,l]\),也就是只管辖一个值,那么其管辖区间的区间和就是 \(a_l\)。
不妨设 \(i\) 号节点所管辖区间的区间和为 \(d_i\)。
由于每个节点的左儿子的管辖范围是该节点管辖范围的左半段,右儿子的管辖范围是该节点管辖范围的右半段。
所以 \(d_i\gets d_{2i}+d_{2i+1}\)。
于是代码就很好写了。
void build(int l,int r,int p){
if(l==r) d[p]=a[l];
else{
int mid=l+((r-l)>>1);
build(l,mid,p<<1);
build(mid+1,r,(p<<1)+1);
d[p]=d[p<<1]+d[(p<<1)+1];
}
}
\(p\) 是现在要建的节点,其管辖范围是 \([l,r]\)。
\(a\) 是操作序列。
3.区间查询
如果要查询 \([l,r]\) 的区间和……
还是递归查询,查询过程中,要维护 \(5\) 个参数:
\(l,r,s,t,p\)。
\(l\) 和 \(r\) 是要查询的区间,在调用过程中不发生改变,\(p\) 是目前查询到的区间,其管辖区间为 \([s,t]\)。
所以 \(\text{query}(l,r,s,t,p)\) 的含义是:
\(\displaystyle{\sum_{i\in [s,t]\cap[l,r]}a[i]}\)
初始时调用 \(\text{query}(l,r,1,n,1)\)。
当查询到 \(p\) 号节点时,如果 \([s,t] \subseteq[l,r]\),直接返回 \(d_p\)。
否则,将 \([s,t]\) 劈成两段,使得左半段和右半段分别为 \(2p\) 的管辖区间和 \(2p+1\) 的管辖区间
然后判断:
- 如果 \([l,r]\) 完全在左半段里,返回 \(\text{query}(l,r,s,mid,p<<1)\)。
- 如果 \([l,r]\) 完全在右半段里,返回 \(\text{query}(l,r,mid+1,t,p<<1|1)\)。
- 如果 \([l,r]\) 横跨左半段与右半段,返回 \(\text{query}(l,r,s,mid,p<<1)+\text{query}(l,r,mid+1,t,p<<1|1)\)。
其中 \(mid=\lfloor\dfrac{s+t}{2}\rfloor\)。
看代码理解。
int query(int l,int r,int s,int t,int p){
if(l<=s&&t<=r) return d[p];
int mid=s+t>>1,S=0;
if(tag[p]) pushdown(s,t,mid,p);
if(l<=mid) S+=query(l,r,s,mid,p<<1);
if(r>mid) S+=query(l,r,mid+1,t,(p<<1)+1);
return S;
}
代码第 \(4\) 行后面再说,先不用管。
4.单点修改
与树状数组的逻辑相似,修改一个值相当于在树上修改一条链。
与树状数组不同的是,在线段树上修改一条链时,需要从树根往下修改。
每次看要修改的下标是在左区间还是右区间,然后修改左儿子或右儿子,直到修改到叶子为止。
代码比树状数组容易理解多了。
void update(int l,int r,int p,int pos,int c){
if(l==r){
d[p]+=c;
return ;
}
int mid=(l+r)>>1;
if(pos<=mid) update(l,mid,p<<1,pos,c);
else update(mid+1,r,p<<1|1,pos,c);
pushup(p);
}
\(p\) 是现在正在修改的点的序号,其管辖范围为 \([l,r]\)。
要将 \(a_{pos}\) 加上 \(c\)。
发现代码的第二行直接就判断 \(l=r\) ,为什么不用判断 \(l = r = pos\) 呢?因为显然 \(l=r\) 的时候就已经也等于 \(pos\) 了。
还有最后的 pushup 。
当然可以直接写 \(d_p\gets d_{2p}+d_{2p+1}\)。
但是大部分时候线段树不是只维护一个区间和,还有维护区间积,区间最值……此时专门设一个函数来整合左右儿子信息会让程序更加有条理。
5.区间修改(暴力)
比如说将 \(a_l\) 到 \(a_r\) 全部加 \(c\) 。
直接做 \(r -l+1\) 次单点修改,每次修改复杂度 \(\Theta(n\log n)\),白白加了一个 \(\log\) ,还不如啥数据结构都没有直接暴力扫。
6.懒惰标记
我太弱了,学到第二遍才把这玩意学会(
主体思路与区间查询有点像,就是要写这么一个函数:
update(int l,int r,int s,int t,int p,int c)
即 \(\forall i\in[l,r] \cap[s,t],a_i\gets a_i+c\),其中 \([s,t]\) 为节点 \(p\) 的管辖区间。
初始时调用 \(\text{update}(l,r,1,n,1,c)\)。
当 \([s,t]\subseteq[l,r]\) 时,从 \(a_s\) 到 \(a_t\) 每一个值都会加上 \(c\) ,那么 \(d_p\) 的值就要加上 \(c\times(t-s+1)\) 。
\(p\) 的所有子树里的点的权值都要发生改变,总不能 \(\Theta(n)\) 递归地全改一遍吧,于是引入:
懒惰标记 (tag)
先看一下它的实现,然后就知道为什么它“懒惰”了。
\(d_p\) 的值就要加完 \(c\times(t-s+1)\) 之后,我们让 \(tag_p\) 也加上一个 \(c\) ,然后就不用管子树了,直接 return。
下次查询/修改的时候,如果查询/修改到节点 \(p\) ,发现。
\(tag_p\) 不为0,于是就将左儿子和右儿子处理一下,把 tag 下传,然后清空自己的 tag ,这个左儿子和右儿子的标记下放与处理,主要靠一个 pushdown 函数来实现。
所以 \(tag_p\) 的作用就是声明节点 \(p\) 管辖区间的所有值都要加上一个 \(c\) ,最后相当于一个延后处理的思想。
inline void pushdown(int s,int t,int mid,int p){
d[p<<1]+=tag[p]*(mid-s+1);
d[p<<1|1]+=tag[p]*(t-mid);
tag[p<<1]+=tag[p];
tag[p<<1|1]+=tag[p];
tag[p]=0;
}
其中 \(mid=\lfloor\dfrac{s+t}{2}\rfloor\)。
update 的代码:
void add(int l,int r,int c,int s,int t,int p){
if(l<=s&&t<=r){
d[p]+=(t-s+1)*c;
tag[p]+=c;
return ;
}
int mid=s+((t-s)>>1);
if(tag[p]) pushdown(s,t,mid,p);
if(l<=mid) add(l,r,c,s,mid,p<<1);
if(r>mid) add(l,r,c,mid+1,t,(p<<1)+1);
d[p]=d[p<<1]+d[(p<<1)+1];
}
线段树完整代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=500005;
class SegmentTree{
private:
int d[N],tag[N],a[N];
inline void pushdown(int s,int t,int m,int p){
d[p<<1]+=tag[p]*(m-s+1);
d[(p<<1)+1]+=tag[p]*(t-m);
tag[p<<1]+=tag[p];
tag[(p<<1)+1]+=tag[p];
tag[p]=0;
}
void build(int l,int r,int p){
if(l==r) d[p]=a[l];
else{
int mid=l+((r-l)>>1);
build(l,mid,p<<1);
build(mid+1,r,(p<<1)+1);
d[p]=d[p<<1]+d[(p<<1)+1];
}
}
int query(int l,int r,int s,int t,int p){
if(l<=s&&t<=r) return d[p];
int mid=s+((t-s)>>1),S=0;
if(tag[p]) pushdown(s,t,mid,p);
if(l<=mid) S+=query(l,r,s,mid,p<<1);
if(r>mid) S+=query(l,r,mid+1,t,(p<<1)+1);
return S;
}
void add(int l,int r,int c,int s,int t,int p){
if(l<=s&&t<=r){
d[p]+=(t-s+1)*c;
tag[p]+=c;
return ;
}
int mid=s+((t-s)>>1);
if(tag[p]&&s!=t) pushdown(s,t,mid,p);
if(l<=mid) add(l,r,c,s,mid,p<<1);
if(r>mid) add(l,r,c,mid+1,t,(p<<1)+1);
d[p]=d[p<<1]+d[(p<<1)+1];
}
public:
inline void fun(int n,int m){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,n,1);
for(int i=1;i<=m;i++){
int op;
cin>>op;
if(op==1){
int x,y,z;
cin>>x>>y>>z;
add(x,y,z,1,n,1);
}
else{
int x,y;
cin>>x>>y;
cout<<query(x,y,1,n,1)<<endl;
}
}
}
}st;
int n,m;
signed main(){
ios::sync_with_stdio(false);
st.fun(n,m);
return 0;
}
用类“封装”了一下,为了好看。
这个是 【模板】线段树1 的 AC 代码。
7.结构体版线段树
代码逻辑和正常的线段树是一模一样的,只是这样写更易于扩展。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=500005;
class SegmentTree{
private:
struct ST{
int d,tag;
}st[N];
int a[N];
inline void pushdown(int s,int t,int m,int p){
st[p<<1].d+=st[p].tag*(m-s+1);
st[(p<<1)+1].d+=st[p].tag*(t-m);
st[p<<1].tag+=st[p].tag;
st[(p<<1)+1].tag+=st[p].tag;
st[p].tag=0;
}
void build(int l,int r,int p){
if(l==r) st[p].d=a[l];
else{
int mid=l+((r-l)>>1);
build(l,mid,p<<1);
build(mid+1,r,(p<<1)+1);
st[p].d=st[p<<1].d+st[(p<<1)+1].d;
}
}
int query(int l,int r,int s,int t,int p){
if(l<=s&&t<=r) return st[p].d;
int mid=s+((t-s)>>1),S=0;
if(st[p].tag) pushdown(s,t,mid,p);
if(l<=mid) S+=query(l,r,s,mid,p<<1);
if(r>mid) S+=query(l,r,mid+1,t,(p<<1)+1);
return S;
}
void add(int l,int r,int c,int s,int t,int p){
if(l<=s&&t<=r){
st[p].d+=(t-s+1)*c;
st[p].tag+=c;
return ;
}
int mid=s+((t-s)>>1);
if(st[p].tag&&s!=t) pushdown(s,t,mid,p);
if(l<=mid) add(l,r,c,s,mid,p<<1);
if(r>mid) add(l,r,c,mid+1,t,(p<<1)+1);
st[p].d=st[p<<1].d+st[(p<<1)+1].d;
}
public:
inline void fun(int n,int m){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,n,1);
for(int i=1;i<=m;i++){
int op;
cin>>op;
if(op==1){
int x,y,z;
cin>>x>>y>>z;
add(x,y,z,1,n,1);
}
else{
int x,y;
cin>>x>>y;
cout<<query(x,y,1,n,1)<<endl;
}
}
}
}seg;
int n,m;
signed main(){
ios::sync_with_stdio(false);
seg.fun(n,m);
return 0;
}
8.动态开点线段树
线段树的空间要开到 \(4n\),而动态开点线段树的逻辑是只建需要访问的节点,代码也很简单,就是开始的时候只有一个根节点,查询或修改的时候如果没有左/右儿子就直接新建一个,注意此时 \(p\) 的左右儿子就不一定是 \(2p\) 和 \(2p+1\)。需要专门两个数组来记录。
其实这个东西暂时不用理会,等到说到权值线段树的时候再提。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=200005;
class SegmentTree{
private:
int d[N],tag[N],cnt=1,ls[N],rs[N];
inline void pushup(int &p) {
d[p]=d[ls[p]]+d[rs[p]];
}
inline void pushdown(int s,int t,int m,int p){
if(!ls[p]) ls[p]=++cnt;
if(!rs[p]) rs[p]=++cnt;
d[ls[p]]+=tag[p]*(m-s+1);
d[rs[p]]+=tag[p]*(t-m);
tag[ls[p]]+=tag[p];
tag[rs[p]]+=tag[p];
tag[p]=0;
}
void build(int l,int r,int &p,int u,int v){
if(!p) p=++cnt;
if(l==r) d[p]=v;
else{
int mid=l+((r-l)>>1);
if(u<=mid) build(l,mid,ls[p],u,v);
else build(mid+1,r,rs[p],u,v);
pushup(p);
}
}
int query(int l,int r,int s,int t,int p){
if(!p) return 0;
if(l<=s&&t<=r) return d[p];
int mid=s+((t-s)>>1),S=0;
if(tag[p]) pushdown(s,t,mid,p);
if(l<=mid) S+=query(l,r,s,mid,ls[p]);
if(r>mid) S+=query(l,r,mid+1,t,rs[p]);
return S;
}
void add(int l,int r,int c,int s,int t,int &p){
if(!p) p=++cnt;
if(l<=s&&t<=r){
d[p]+=(t-s+1)*c;
tag[p]+=c;
return ;
}
int mid=s+((t-s)>>1);
if(tag[p]) pushdown(s,t,mid,p);
if(l<=mid) add(l,r,c,s,mid,ls[p]);
if(r>mid) add(l,r,c,mid+1,t,rs[p]);
pushup(p);
}
public:
inline void fun(int n,int m){
cin>>n>>m;
for(int i=1;i<=n;i++){
int tmp=1,x;
cin>>x;
build(1,n,tmp,i,x);
}
for(int i=1;i<=m;i++){
int op;
cin>>op;
if(op==1){
int x,y,z,tmp=1;
cin>>x>>y>>z;
add(x,y,z,1,n,tmp);
}
else{
int x,y;
cin>>x>>y;
cout<<query(x,y,1,n,1)<<endl;
}
}
}
}st;
int n,m;
signed main(){
ios::sync_with_stdio(false);
st.fun(n,m);
return 0;
}
写的好像有点问题,但是能过。
9.最大子段和
给一个序列,单点修改,每次询问给一个 \(l,r\),要在 \([l,r]\) 内找到一段连续的和最大的区间,输出这个和。
注意是单点修改,如果是区间修改的话好像要用什么“KTT”,太高深了,黑题。
此处一个线段树足矣。
每个节点要维护 \(4\) 个信息:
\(lans\),\(rans\),\(ans\),\(d\)。
让我分别来解释一下(这里用结构体版线段树来写)。
\(st_{p,lans}: p\) 的管辖区间中经过左端点的最大子段和。
\(st_{p,rans}: p\) 的管辖区间中经过右端点的最大子段和。
\(st_{p,ans}: p\) 的管辖区间中最大子段和。
\(st_{p,d}:p\) 的管辖区间中的区间和。
然后,build 和 update 都很简单,和正常线段树没啥区别。
主要 pushup 和 query 要重点说一下。
① pushup
区间和就直接把左儿子和右儿子的区间和加起来就行了。
设节点 \(p\) 的管辖区间为 \([s,t]\) ,\(2p\) 的管辖区间是 \([s,mid]\),\(2p+1\) 的管辖区间是 \([mid+1,t]\) 。
那么 \(st_{p,lans}\),即
分为 \(2\) 种情况:
- \(r\le mid\)
- \(r>mid\)
对于第一种情况,
st[p].lans = st[p<<1].d+st[p<<1|1].lans
对于第二种情况,
st[p].lans = st[p<<1].lans
所以
st[p].lans = max(st[p<<1].d+st[p<<1|1].lans,st[p<<1].lans)
同理,对于 \(rans\) ,有
st[p].rans = max(st[p<<1|1].d+st[p<<1].rans,st[p<<1|1].rans)
现在主要处理 \(st_{p,ans}\) ,即为:
其中 \(p\) 的管辖区间为 \([s,t]\)。
分为 \(3\) 种情况:
- \(r\le mid\)
- \(l>mid\)
- \(l\le mid<r\)
对于第一种情况,
st[p].ans = st[p<<1].ans
对于第二种情况,
st[p].ans = st[p<<1|1].ans
对于第三种情况,
st[p].ans = st[p<<1].rans + st[p<<1|1].lans
所以
st[p].ans = max(max(resl.ans , resr.ans) , resl.rans + resr.lans)
这里重点说一下第三种情况,即和为最大子段和的区间横跨了\(p\) 的管辖区间的左半段和右半段。

这个区间(即 \([l,r]\) )在 \(mid\) 前的部分因为右端点是 \(mid\) 且满足局部最优,所以它的区间和等于 \(st_{2p,rans}\)。
同理,这个区间在 \(mid\) 后的部分的区间和等于 \(st_{2p+1,lans}\)。
所以在这种情况下 \([l,r]\) 的区间和为 \(st_{2p,rans} + st_{2p+1,lans}\)。
最后贴一下 pushup 的代码:
inline SegmentTree pushup(SegmentTree &res,SegmentTree &resl,SegmentTree &resr) {
res.d=resl.d+resr.d;
res.lans=max(resl.lans,resl.d+resr.lans);
res.rans=max(resr.rans,resr.d+resl.rans);
res.ans=max(max(resl.ans,resr.ans),resl.rans+resr.lans);
return res;
}
稍微解释一下,SegmentTree 是结构体名。
还有,此处 pushup 的参数不是简单的一个 \(p\) ,也就是说在 build 和 update 中执行 pushup 的时候就不是简单地调用
pushup(p)
而是
st[p]=pushup(st[p],st[p<<1],st[p<<1|1])
为什么要如此,其实是为了 query 更方便。
②query
query 在此处返回的是一个 SegmentTree 类型的变量,每次询问输出
\(\text{query}(l,r,1,n,1)_{ans}\)。
l,r,是询问区间的端点,\(\text{query}(l,r,s,t,p)\) 的概念是。
\([l,r]\cap[s,t]\) 的最大子段和,其中 \([s,t]\) 为节点 \(p\) 的管辖区间。
当 \([s,t]\subseteq[l,r]\) 时,返回 \(st_{p,ans}\)。
设\(mid=\lfloor\dfrac{s+t}{2}\rfloor\),
特别地,
当 \([l,r]\subseteq[s,mid]\) 时,返回
query(l,r,s,mid,p<<1)
当 \([l,r]\subseteq[mid+1,t]\) 时,返回
query(l,r,mid+1,t,p<<1|1)
如果前面这几种情况都不满足,那么表明 \([l,r]\) 横跨了 \([s,t]\) 的左半段与右半段,于是将 \([l,r]\) 以 \(mid\) 为分界点劈成两段,分别查询这两段的答案,即:
query(l,r,s,mid,p<<1)
以及
query(l,r,mid+1,t,p<<1|1)
设它们俩分别为 \(tmpl\),\(tmpr\),最后用 pushup 把它们合并起来得到一个 \(res\) 返回即可。
即:
SegmentTree tmpl,tmpr,res;
tmpl=query(l,r,s,mid,p<<1);
tmpr=query(l,r,mid+1,t,p<<1|1);
return pushup(res,tmpl,tmpr);
这也就是我要把 pushup 写成三个参数形式的原因。
最后的最后,上代码。(AC code of SP1716)
~={red}PLEASE DO NOT COPY=~
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=4000005;
struct SegmentTree{
int d,lans,rans,ans;
SegmentTree(){
d=0;
lans=rans=ans=-1e18;
}
}st[N];
int a[N];
inline SegmentTree pushup(SegmentTree &res,SegmentTree &resl,SegmentTree &resr) {
res.d=resl.d+resr.d;
res.lans=max(resl.lans,resl.d+resr.lans);
res.rans=max(resr.rans,resr.d+resl.rans);
res.ans=max(max(resl.ans,resr.ans),resl.rans+resr.lans);
return res;
}
SegmentTree query(int l,int r,int s,int t,int p){
if(l<=s&&t<=r) return st[p];
int mid=s+((t-s)>>1);
if(r<=mid) return query(l,r,s,mid,p<<1);
if(l>mid) return query(l,r,mid+1,t,p<<1|1);
SegmentTree tmpl,tmpr,res;
tmpl=query(l,r,s,mid,p<<1);
tmpr=query(l,r,mid+1,t,p<<1|1);
return pushup(res,tmpl,tmpr);
}
void add(int l,int c,int s,int t,int p){
if(s==t){
st[p].lans=st[p].rans=st[p].d=st[p].ans=c;
return ;
}
int mid=s+((t-s)>>1);
if(l<=mid) add(l,c,s,mid,p<<1);
else add(l,c,mid+1,t,p<<1|1);
st[p]=pushup(st[p],st[p<<1],st[p<<1|1]);
}
void build(int l,int r,int p){
if(l==r){
st[p].lans=st[p].rans=st[p].d=st[p].ans=a[l];
return ;
}
int mid=l+((r-l)>>1);
build(l,mid,p<<1);
build(mid+1,r,p<<1|1);
st[p]=pushup(st[p],st[p<<1],st[p<<1|1]);
}
int n,m;
signed main(){
ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,n,1);
cin>>m;
for(int i=1;i<=m;i++){
int op;
cin>>op;
if(!op){
int x,y;
cin>>x>>y;
add(x,y,1,n,1);
}
else{
int x,y;
cin>>x>>y;
cout<<query(x,y,1,n,1).ans<<endl;
}
}
return 0;
}
我们对线段树的理解通过此题又加深了一步,query 事实上也是需要“广义的 pushup”的。
10.其他
I.区间加 区间乘 区间求和
显而易见地,我们需要维护 \(2\) 个 \(tag\): 加法标记与乘法标记。
那么这两个标记先执行那个呢?
我们知道 \((a+b)\times c=ac+bc\)。
所以当一个数 \(a\) 被先加上一个值再乘上一个值时我们可以把它转换为先乘后加。
而 \(a\times b+c\) 却不能简单地转化为一个先加再乘的形式。
所以要先执行乘法标记,再执行加法标记。
要注意的是,为了用乘法分配律将先加再乘转为先乘再加,在执行/下放乘法标记时,应该将区间和与加法标记都乘以乘法标记的值。
这个方法有一点绕,但是它的思想确实是非常好的。
II 非常数复杂度合并
参见 P4198 ,它的 pushup 是 \(\Theta(logn)\) 的,思维精巧,好题。
III 操作使得序列中的值变小很多
比如说要实现区间开方(下取整) 区间求和,保证全为正数。
开方操作难以用简单的一个懒惰标记来实现。
但是我们可以注意力惊人地发现 \(10^9\) 以内的数最多开方 \(6\) 到 \(7\) 次就可以变为 \(1\),并且一个正数无论如何开方也无法变为 \(0\)。
于是维护一个区间最大值,如果它等于 \(1\),说明这个区间所有数都是 \(1\),那么它的和就是它的长度。
如果最大值不是 \(1\),就直接暴力加。
复杂度我也不知道为什么就是 \(\Theta(q\log n)\),\(q\) 是询问/操作个数。
此题是
Luogu P4145
按照这种思想,我们可以处理区间除区间求和等问题……





 浙公网安备 33010602011771号
浙公网安备 33010602011771号