一道好好的数据结构题,有的出题人会把它放在树上来强迫选手写树剖。
例题引入:有根树上 \(n\) 个点有点权,\(4\) 种操作:
1. 将一条链上的所有点加上一个值。
2.查询一条链的点权和。
3.将一棵子树的所有点加上一个值。
4.查询一棵子树的点权和。
(注意:本文中某个节点的“子树”包含该节点)
1. 朴素做法
暴力 ,挨个修改子树/链上的每一个值。
如果有 \(q\) 次操作/询问,那么复杂度就是 \(\Theta(qn\log n)\) 。
其中那个 \(\log\) 是 LCA 带的。
2. 结构
看到这些操作,长得就像线段树,所以考虑线段树。
树链剖分主要分为:
- 重链剖分
- 长链剖分
- 实链剖分(LCT 用)
可能还有别的,但我太菜了不知道……
通常情况下,我们说“树链剖分”都是指重链剖分。
我们知道线段树只能处理序列问题。
所以树链剖分就要帮线段树把树“剖”成一个序列。
总体上来说,树链剖分就是一个插件,装到线段树上,它就能处理树上问题。
现在的问题是,怎么剖?
我们此时先做几个定义:
- 重子节点:一个节点的子树节点数最多的儿子
- 轻子节点:一个节点的非重子节点儿子
- 重边:这个节点到重子节点的边
- 轻边:其他边
- 重链:若干条首尾衔接的重边

如上图所示。
发现如果这个节点是轻子节点,那么它就是一条重链的顶端,它的逆命题同样正确。
特别地,根是轻子节点。
我们发现了一个性质:假设一个节点 \(R\) 的子树大小为 \(s\),那么该节点的所有轻子节点的子树大小不超过 \(\lfloor \frac s 2\rfloor\)。
这个性质是很显然的,但学过数学分析的看不惯“显然”二字,故略证:
反证,假设存在 \(R\) 的一个轻子节点 \(S\),满足 \(S\) 的子树大小 \(siz_S>\lfloor\dfrac{siz_R}{2}\rfloor\)。
则不存在另一子节点 \(T\) 的子树大小大于 \(\lfloor\dfrac{siz_R}{2}\rfloor\),否则 \(siz_T+siz_S>siz_R\),矛盾。
因此 \(S\) 的子树大小是 \(R\) 的所有儿子里最大的一个。
所以 \(S\) 是重子节点。矛盾!
\(\square\)
所以,树上的任意一条路径上的所有节点最多属于 \(\log n\) 个不同的重链。
证明:
每一条重链的顶部都是一个轻子节点。
每一条从 \(u\) 到 \(v\) 的路径都可以被拆成以 LCA 为分界点的两条子路径。
每条子路径上节点的深度是依次递增的。
假设两条子路径中较长的一条为 \(\Psi\),并使 \(\Psi\) 上的所有节点属于 \(k\) 条重链。
那么 \(\Psi\) 上有 \(k\) 个轻子节点。
每个轻子节点的子树大小都不超过其父节点子树大小的一半。
所以 \(\Psi\) 的末端节点的子树大小 \(S\) 必定小于 \(\dfrac{L}{2^k}\)。
其中 \(L\) 是 LCA 的子树大小,有 \(L\le n\)。
所以有 \(S\le \dfrac{n}{2^k}\)。
又因为自己也是自己子树的一个节点,所以任何节点的子树大小至少是 \(1\)。
所以有 \(1\le\dfrac{n}{2^k}\),又因为 \(\dfrac{n}{2^k}\) 是正数,故 \(2^k\le n\),即 \(k\le \log_2n\)。
\(\square\)
这个不等式其实放得挺宽的,那些能否取等的问题我没有仔细考虑,不过最后至少说明结论是正确的。
所以再带上一个线段树的 \(O(\log n)\),树链剖分的复杂度为 \(O(q\log^2n)\)。
\(q\) 是询问次数。
3. 初始
任何一个树链剖分的程序都需要写 \(2\) 个 DFS。
第一个用来预处理每个节点的:
深度、父亲、子树大小、重儿子。
第二个用来预处理:
每个节点所在重链顶部节点,每个节点的 DFN 序,每个 DFN 序所对应的节点。
第一个 DFS 属于基本操作,普及难度:
void build1(int u){//记录父节点、深度、子树大小、重子节点。
son[u]=-1;
siz[u]=1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa[u]) continue;
dep[v]=dep[u]+1;
fa[v]=u;
build1(v);
siz[u]+=siz[v];
if(son[u]==-1||siz[v]>siz[son[u]]) son[u]=v;
}
}
第二个 DFS 如果掌握了 Tarjan 算法也是极其容易的。
此处说明,一个节点的 DFN 序为该节点在 DFS 的过程中是第几个被访问的。
只不过还有一个要求是同一重链上的节点的 DFN 序必须连续。
于是每次递归时先递归重子节点即可。
至于为什么要满足这个性质,我们到下一部分来说。
void build2(int u,int tp){
top[u]=tp;
dfn[u]=++num;
a[num]=at[u];
rnk[dfn[u]]=u;
if(son[u]==-1) return ;
build2(son[u],tp);
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(son[u]!=v&&v!=fa[u]) build2(v,v);
}
}
注意一下,\(rnk_i\) 代表的是 DFN 序为 \(i\) 的节点的编号。
还有就是 \(at_i\) 表示编号为 \(i\) 的节点的点权,\(a_i\) 表示 DFN 序为 \(i\) 的节点的点权。
接下来就是树链剖分的精髓。
4. 剖分
树剖,"树"我们已经说得差不多了,接下来就是"剖"。
我们先考虑路径加以及路径求和。
现在我们有一棵线段树和一大堆 DFN 序连续的重链……
是的!我们只需要把这棵线段树“安装”到 DFN 序上就可以了!
如何安装?
假设我们要求从节点 \(u\) 到节点 \(v\) 的路径中的点的点权和。
首先我们知道这条路径一定可以被拆成最多 \(\log n\) 条(可能不完整的)重链,又因为重链内部的 DFN 序连续,所以就相当于以 DFN 序为下标,查询 \(\log n\) 个下标连续的段!
相当于我们将每个点重新编号,以 DFN 序作为其新编号,然后把每个点以新编号从小到大排列起来。然后用线段树来维护。
(我认为已经说得非常清楚了。)
下一步就是,考虑如何拆出这 \(\log n\) 个链。
- 找到 \(u\) 和 \(v\) 所在重链的顶点,即 \(top_u\) 和 \(top_v\)。
- 如果它们不相等,比较这两个顶点的深度,若 \(dep(top_u)<dep(top_v)\),则交换 \(u\) 和 \(v\),使得 \(dep(top_u)>dep(top_v)\),如果相等,则退出循环。
- 用线段树求出 DFN 序从 \(dfn_{top_u}\) 到 \(dfn_u\) 的节点的点权和,也就是从 \(u\) 到 \(top_u\) 的点权和。
- \(u\) 跳到 \(top_u\) 的上面,即 \(u\gets fa_{top_u}\)。
- 返回第一步。
这 \(5\) 步乍一看似乎有些复杂,但只要思路顺着这个代码捋一遍,再自己推一遍,会发现其实特别地简单。
需要提醒的是,在第四步中,\(u\) 不可能跳到 \(u\),\(v\) 的 LCA 的上面。
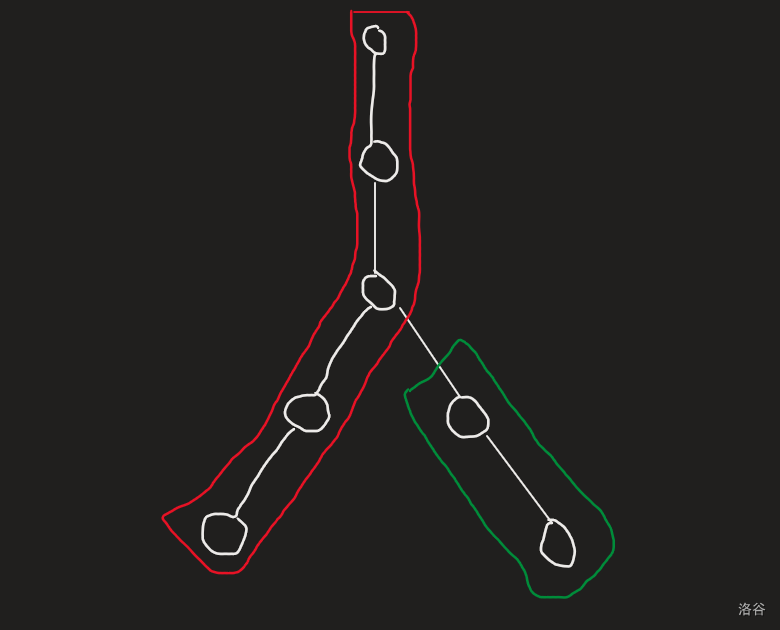
如图,左边红色的是 \(u\) 的重链,右边绿色的是 \(v\) 的重链。
如果 \(u\) 跳到了 LCA 的上面,说明 \(top_v\) 一定是严格处于 LCA 的下面的,此时不满足 \(dep(top_u)>dep(top_v)\) 的条件,矛盾!
好了,现在这一步结束了,\(u\) 和 \(v\) 跳到同一条重链上了,它们之间所有点的 DFN 序是连续的了,直接用线段树把它们之间的点权和加起来就行了。
上代码:
inline int psum(int u,int v){
int res=0;
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]]) swap(u,v);
res+=query(dfn[top[u]],dfn[u],1,n,1);
u=fa[top[u]];
}
if(dep[u]>dep[v]) swap(u,v);
res+=query(dfn[u],dfn[v],1,n,1);
return res;
}
路径加法同理:
inline void pupd(int u,int v,int c){
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]]) swap(u,v);
update(dfn[top[u]],dfn[u],c,1,n,1);
u=fa[top[u]];
}
if(dep[u]>dep[v]) swap(u,v);
update(dfn[u],dfn[v],c,1,n,1);
}
树链剖分最困难的部分结束了,Congratulation!
5. 子树问题
显然,一棵子树内的所有节点的 DFN 序时连续的,且该子树的根的 DFN 序最小。
毕竟做 DFS 的时候就是一棵子树一棵子树地递归嘛!
于是代码极短。
inline int ssum(int u){//子树求和
return query(dfn[u],dfn[u]+siz[u]-1,1,n,1);
}
inline void supd(int u,int c){//子树加法
update(dfn[u],dfn[u]+siz[u]-1,c,1,n,1);
}
放一下完整代码。
#include<bits/stdc++.h>
#define int unsigned long long
using namespace std;
const int N=6e5+10;
struct edge{
int to,nxt;
}e[N<<1];
int n,m,r,mod,fa[N],siz[N],dfn[N],rnk[N],num;
int head[N],cnt,son[N],dep[N],top[N];
class HPD{
private:
int d[N],tag[N],a[N],at[N];
void add(int u,int v){
e[++cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt;
}
void build1(int u){
son[u]=-1;
siz[u]=1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa[u]) continue;
dep[v]=dep[u]+1;
fa[v]=u;
build1(v);
siz[u]+=siz[v];
if(son[u]==-1||siz[v]>siz[son[u]]) son[u]=v;
}
}
void build2(int u,int tp){
top[u]=tp;
dfn[u]=++num;
a[num]=at[u];
rnk[dfn[u]]=u;
if(son[u]==-1) return ;
build2(son[u],tp);
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(son[u]!=v&&v!=fa[u]) build2(v,v);
}
}
inline void pushdown(int s,int t,int m,int p){
d[p<<1]+=tag[p]*(m-s+1);
d[p<<1]%=mod;
d[(p<<1)+1]+=tag[p]*(t-m);
d[(p<<1)+1]%=mod;
tag[p<<1]+=tag[p];
tag[p<<1]%=mod;
tag[(p<<1)+1]+=tag[p];
tag[(p<<1)+1]%=mod;
tag[p]=0;
}
void build(int l,int r,int p){
if(l==r) d[p]=a[l];
else{
int mid=l+((r-l)>>1);
build(l,mid,p<<1);
build(mid+1,r,(p<<1)+1);
d[p]=d[p<<1]%mod+d[(p<<1)+1]%mod;
d[p]%=mod;
}
}
int query(int l,int r,int s,int t,int p){
if(l<=s&&t<=r){
d[p]%=mod;
return d[p];
}
int mid=s+((t-s)>>1),S=0;
if(tag[p]) pushdown(s,t,mid,p);
if(l<=mid){
S+=query(l,r,s,mid,p<<1)%mod;
S%=mod;
}
if(r>mid){
S+=query(l,r,mid+1,t,(p<<1)+1);
S%=mod;
}
return S%mod;
}
void update(int l,int r,int c,int s,int t,int p){
if(l<=s&&t<=r){
d[p]+=(t-s+1)*c;
d[p]%=mod;
tag[p]+=c;
tag[p]%=mod;
return ;
}
int mid=s+((t-s)>>1);
if(tag[p]&&s!=t) pushdown(s,t,mid,p);
if(l<=mid) update(l,r,c,s,mid,p<<1);
if(r>mid) update(l,r,c,mid+1,t,(p<<1)+1);
d[p]=d[p<<1]%mod+d[(p<<1)+1]%mod;
d[p]%=mod;
}
inline int psum(int u,int v){
int res=0;
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]]) swap(u,v);
res+=query(dfn[top[u]],dfn[u],1,n,1);
res%=mod;
u=fa[top[u]];
}
if(dep[u]>dep[v]) swap(u,v);
res+=query(dfn[u],dfn[v],1,n,1);
res%=mod;
return res;
}
inline void pupd(int u,int v,int c){
c%=mod;
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]]) swap(u,v);
update(dfn[top[u]],dfn[u],c,1,n,1);
u=fa[top[u]];
}
if(dep[u]>dep[v]) swap(u,v);
update(dfn[u],dfn[v],c,1,n,1);
}
inline int ssum(int u){
return query(dfn[u],dfn[u]+siz[u]-1,1,n,1)%mod;
}
inline void supd(int u,int c){
c%=mod;
update(dfn[u],dfn[u]+siz[u]-1,c,1,n,1);
}
public:
inline void fun(){
cin>>n>>m>>r>>mod;
for(int i=1;i<=n;i++) cin>>at[i];
for(int i=1;i<n;i++){
int x,y;
cin>>x>>y;
add(x,y);
add(y,x);
}
build1(r);
build2(r,r);
build(1,n,1);
for(int i=1;i<=m;i++){
int op;
cin>>op;
if(op==1){
int x,y,z;
cin>>x>>y>>z;
pupd(x,y,z);
}
else if(op==2){
int x,y;
cin>>x>>y;
cout<<psum(x,y)<<"\n";
}
else if(op==3){
int x,z;
cin>>x>>z;
supd(x,z);
}
else if(op==4){
int x;
cin>>x;
cout<<ssum(x)<<"\n";
}
}
}
}st;
signed main(){
ios::sync_with_stdio(false);
st.fun();
return 0;
}
可以注意到,在 build 中我们是对数组 \(a\) 建立的线段树,而 \(a_i\) 又代表的是 DFN 序为 \(i\) 的节点的点权。所以也就是说树链剖分所维护的那颗线段树是以 DFN 序作为每个点的“编号“的。
这是 P3384 的 AC 代码。
\(\color{red}{\text{PLEASE DO NOT COPY.}}\)
6. 边权处理
我们发现,树链剖分的模板是维护点权,那么边权该如何处理?譬如说,查询从 \(u\) 到 \(v\) 的路径和。
其实这是非常容易的。
我们知道除了根,所有的节点都只有一个父节点,也就是说每条边与其下方的点可以一一对应。
于是每条边的边权都可以转化为其下方连的点的点权。
如果转化为上方的点的点权的话,那么一个点因为可能有多个儿子,所以可能要表示多条边的边权,这当然是不可以的。
然后就愉快地转化为点权问题了!
最后有一个需要注意的点,在处理 \(u\) 到 \(v\) 的路径和时,要忽略它们的 LCA 的点权!(此处“点权”指从边权转化过来的点权)
如图:
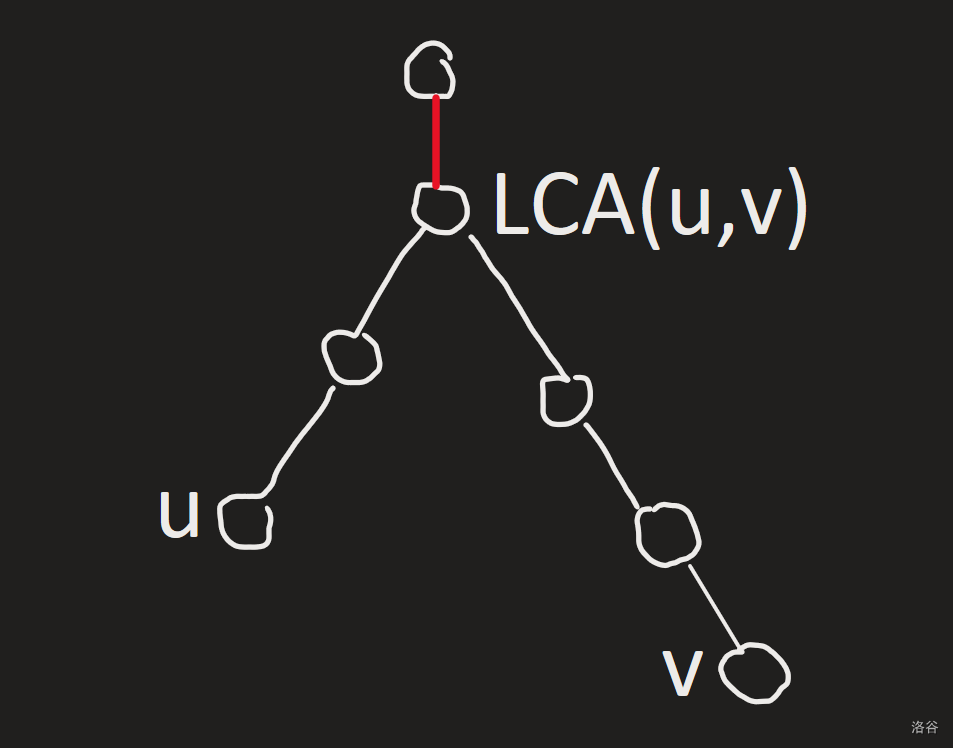
LCA 的点权所对应的边的边权是那条红色边的边权,但它并不在要查询的路径上。
那么如何把它规避掉?
我们知道,很显然地,LCA 的是这条路径中 DFN 序最小的一个。
而跳完重链后, \(u\) 和 \(v\) 已经在同一重链上时,它们中必有一个是原先的 LCA。
原因是重链必定是直直地从上往下的,不可能在某一点“拐弯”。
我们之前处理点权时路径求和的代码的最后一步是这样的:
if(dep[u]>dep[v]) swap(u,v);
res+=query(dfn[u],dfn[v],1,n,1);
return res;
swap 完了之后保证了 \(u\) 的 DFN 序小于 \(v\) 的 DFN 序,因此现在的 \(u\) 就是原先的 LCA。
我们假设现在 \(u\) 的 DFN 序是 \(d\),那么 DFN 序为 \(d+1\) 的那个点就既是 \(u\) 的儿子,又是处于现在的 \(u\) 和 \(v\) 之间的路径上的。
所以最后的询问就改为:
res+=query(dfn[u]+1,dfn[v],1,n,1);
即可。这样就既保证了 LCA 被规避掉,又计入了所有该被计入的节点。
此时可能会有疑问:如果跳完重链之后,\(u\) 直接就等于 \(v\) 了,那么 \(dfn_u+1\) 不就大于 \(dfn_v\) 了吗?
其实无需担心。
跳重链之后不可能有 \(u=v\) 的情况。
否则 LCA 就会引出 \(2\) 条重链了!这不可能!
最后,如果既有点权又有边权,那么开 \(2\) 棵线段树就好了。
7. 维护不可交换信息
建议先学习线段树最大子段和,了解不可交换的 pushup 的原理。
我们先前说,如果要统计路径和的话,直接把路径拆成重链然后把重链的和加起来就完了。
这是因为加法具有交换律,即 \(a+b=b+a\)。
但是现在有这么一个问题:
树上的每一个节点都有一个颜色。
每次修改将某条路径的所有点染成某个颜色。
每次询问某条路径上的连续颜色段数。
比如,序列1111233112231113就有 \(8\) 个颜色段,分别为:
1111,2,33,11,22,3,111,3。
(SDOI 2011 染色)
先退化为一条链上的问题,很简单,线段树的每个节点维护 \(3\) 个值就够了。
它们分别为该节点管辖区间的:左端点的颜色(\(l\))、右端点的颜色(\(r\))、连续颜色段数(\(ans\))。
修改和懒标记的下放都非常的简单,把连续颜色段数改成 \(1\),左右端点颜色改成将要染上的颜色即可。
pushup 的时候考虑左区间右端点的颜色与右区间左端点的颜色是否相同。(好长的一句话)
相同的话就代表着中间的两段颜色可以合并成一段,合并后节点的 \(ans\) 就是左右区间的 \(ans\) 之和再减去 \(1\)。
代码:
inline void pushup(node &res,node resl,node resr){
if(resl.r==resr.l) res.d=resl.d+resr.d-1;
else res.d=resl.d+resr.d;
res.l=resl.l;
res.r=resr.r;
}
还是挺简单的。
为了解决这个问题在树上的版本,我们先做几个定义(我自己编的):
定义一条从 \(u\) 到 \(v\) 的路径可以被拆成最多 \(3\) 个路径段:
- 左路径:从 \(u\) 到 LCA 的路径中除 LCA 之外的部分。
- 右路径:从 \(v\) 到 LCA 的路径中除 LCA 之外的部分。
- LCA:\(u\) 和 \(v\) 的最近公共祖先。
这个“路径段”很重要!一定要理解它的意思!
我们知道,本题的 pushup 是不可交换的,换句话说,\(a\) 和 \(b\) 进行合并的结果与 \(b\) 和 \(a\) 进行合并的结果是不一样的。
那么我们处理完某条重链的答案后,如何“加“到总答案里面去?
我们需要知道上一个被处理的重链处于的路径段与此次处理的重链所在的路径段是否相同。
如果不相同:
说明这两条重链不相接,于是就不用管,直接加;
如果相同,那么我们考察:
已知跳重链是从下往上跳的,而越往下的节点 DFN 序越大。
也就是说此次处理的重链一定是接在上次处理的重链的“左边”的。
于是我们就需要关注此次处理的重链的“右端点“与上次处理的重链的“左端点”是否颜色相等。
如果相等,把此次的答案加到总答案里然后减一。同 pushup。
注意,刚才说的所谓“左”,“右”,都是在以 DFN 序为下标的序列,即线段树所维护的那个序列上所考虑的。
好了,现在返回去,是时候该想想怎么判断上一个被处理的重链处于的路径段与此次处理的重链所在的路径段是否相同了。
简单!开两个变量 \(ans1\),\(ans2\),分别记录:
现在的路径段上的前一个被处理的重链的左端点的颜色,
另一个路径段上的前一个被处理的重链的右端点的颜色。
最后 LCA 再单独处理——它与两个路径段都相接。
Talk is cheap. Show me your code.
int ask(int u,int v){
int res=0;
int ans1=-1,ans2=-1;
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]]) swap(u,v),swap(ans1,ans2);
node tmp=query(dfn[top[u]],dfn[u],1,n,1);
res+=tmp.d;
if(tmp.r==ans1) res--;
ans1=tmp.l;
u=fa[top[u]];
}
if(dfn[u]>dfn[v]) swap(u,v),swap(ans1,ans2);
node tmp=query(dfn[u],dfn[v],1,n,1);
res+=tmp.d;
if(tmp.l==ans1) res--;
if(tmp.r==ans2) res--;
return res;
}
第五行中,\(u\) 和 \(v\) 互换了。这说明这次要处理的重链相较于上次改变了路径段,于是 \(ans1\) 和 \(ans2\) 自然也要互换。
其他的有什么问题就看代码吧。
#include<bits/stdc++.h>
using namespace std;
namespace Opshacom{
const int N=100005;
int n,m;
struct edge{
int to,nxt;
}e[N<<1];
int head[N],cnt;
inline void add(int u,int v){
e[++cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt;
}
class HPD{
private:
struct node{
int d,tag,l,r;
bool is;
}st[N<<2];
inline void pushup(node &res,node resl,node resr){
if(resl.r==resr.l) res.d=resl.d+resr.d-1;
else res.d=resl.d+resr.d;
res.l=resl.l;
res.r=resr.r;
}
inline void pushdown(int p,int l,int r,int mid){
if(st[p].is){
st[p<<1].is=st[p<<1|1].is=1;
st[p<<1].d=st[p<<1|1].d=1;
st[p<<1].l=st[p<<1|1].l=st[p].tag;
st[p<<1].r=st[p<<1|1].r=st[p].tag;
st[p<<1].tag=st[p<<1|1].tag=st[p].tag;
st[p].tag=st[p].is=0;
}
}
public:
int dep[N],num,dfn[N],a[N],at[N],fa[N],sz[N],top[N],son[N];
void build(int l,int r,int p){
if(l==r){
st[p].d=1;
st[p].l=st[p].r=a[l];
return ;
}
int mid=(l+r)>>1;
build(l,mid,p<<1);
build(mid+1,r,p<<1|1);
pushup(st[p],st[p<<1],st[p<<1|1]);
}
void update(int l,int r,int s,int t,int p,int c){
if(l<=s&&t<=r){
st[p].d=1;
st[p].l=st[p].r=c;
st[p].tag=c;
st[p].is=1;
return;
}
int mid=(s+t)>>1;
pushdown(p,s,t,mid);
if(l<=mid) update(l,r,s,mid,p<<1,c);
if(r>mid) update(l,r,mid+1,t,p<<1|1,c);
pushup(st[p],st[p<<1],st[p<<1|1]);
}
node query(int l,int r,int s,int t,int p){
if(l<=s&&t<=r) return st[p];
int mid=(s+t)>>1;
pushdown(p,s,t,mid);
if(r<=mid) return query(l,r,s,mid,p<<1);
if(l>mid) return query(l,r,mid+1,t,p<<1|1);
node tmp1=query(l,r,s,mid,p<<1);
node tmp2=query(l,r,mid+1,t,p<<1|1);
node res;
pushup(res,tmp1,tmp2);
return res;
}
void build1(int u){
sz[u]=1;
son[u]=-1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa[u]) continue;
fa[v]=u;
dep[v]=dep[u]+1;
build1(v);
sz[u]+=sz[v];
if(son[u]==-1||sz[v]>sz[son[u]]) son[u]=v;
}
}
void build2(int u,int tp){
top[u]=tp;
dfn[u]=++num;
a[dfn[u]]=at[u];
if(son[u]==-1) return ;
build2(son[u],tp);
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v!=fa[u]&&v!=son[u]) build2(v,v);
}
}
void change(int u,int v,int c){
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]]) swap(u,v);
update(dfn[top[u]],dfn[u],1,n,1,c);
u=fa[top[u]];
}
if(dfn[u]>dfn[v]) swap(u,v);
update(dfn[u],dfn[v],1,n,1,c);
}
int ask(int u,int v){
int res=0;
int ans1=-1,ans2=-1;
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]]) swap(u,v),swap(ans1,ans2);
node tmp=query(dfn[top[u]],dfn[u],1,n,1);
res+=tmp.d;
if(tmp.r==ans1) res--;
ans1=tmp.l;
u=fa[top[u]];
}
if(dfn[u]>dfn[v]) swap(u,v),swap(ans1,ans2);
node tmp=query(dfn[u],dfn[v],1,n,1);
res+=tmp.d;
if(tmp.l==ans1) res--;
if(tmp.r==ans2) res--;
return res;
}
}tr;
inline void work(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>tr.at[i];
for(int i=1;i<n;i++){
int x,y;
cin>>x>>y;
add(x,y);
add(y,x);
}
tr.build1(1);
tr.build2(1,1);
tr.build(1,n,1);
while(m--){
char op;
int u,v,w;
cin>>op;
if(op=='C'){
cin>>u>>v>>w;
tr.change(u,v,w);
}
else{
cin>>u>>v;
cout<<tr.ask(u,v)<<"\n";
}
}
}
}
int main(){
ios::sync_with_stdio(false);
Opshacom::work();
return 0;
}
至于其他的问题也是同一个道理,维护 \(ans1\) 和 \(ans2\),然后考虑合并。
譬如说路径最大子段和,路径上统计相邻同色点对,还有很多……





 浙公网安备 33010602011771号
浙公网安备 33010602011771号