建议先学习平衡树,这样会对一些复杂的树操作理解地更快、更好一些。
零、前言
网上和 OI-wiki 上对于主席树的介绍大多较简洁,对我这种入门水平选手非常不友好。
于是写一篇十分拙劣的面向普及的主席树。
一、简述
主席树,目前最普遍的说法是将它解释为“可持久化权值线段树“,因其发明人缩写为“HJT”而得名。
分析它的名字:
- 首先,线段树。
说明它是 Leafty 的,也就是说,每个单个数据的信息都存在叶子节点内,剩下的节点存的都是整合左右儿子的信息。
比如说,线段树、树状数组都是 Leafty 的。而二叉搜索树就不是,因为它的每个节点都存着一个单个的数据信息。这个表述或许有些难懂,不过感性理解还是挺容易的。 - 然后,权值。
意思是说,它维护的是值域,而不是下标。
也就是说,它存的是每个值所对应的数集中的数的个数。
举个例子,假设某个数组 \(a\) 是 \(\{1,5,3,6,4,2,3,4,1,1,1\}\) ,那么我们根据 \(a\) 来建立一个 \(c\) 数组,\(c_i\) 定义为数字 \(i\) 在 \(a\) 中的出现次数。于是 \(c\) 就是 \(\{4,1,2,2,1,1\}\)(以 \(1\) 为开头)。
那么,普通线段树相当于维护的是 \(a\) 数组,权值线段树维护的是 \(c\) 数组。
换句话说,权值线段树不关心数字在原序列中的先后顺序,只关心它们具体的值。
从这点上来说,我们可以理解为普通线段树维护序列,权值线段树维护集合。 - 最后,可持久化。
可持久化通常分为部分可持久化和完全可持久化。
部分可持久化是指所有的历史版本都可以访问,但不能修改。(除最新版本之外)
完全可持久化是指所有的历史版本既可以访问,也可以修改。
所谓“历史版本”,就是曾经该数据结构的一个状态。
连起来,“可持久化权值线段树”得名。
二、暴力保留历史版本
我们先考虑普通的“可持久化线段树“。
已知普通的线段树每次修改时就会覆盖掉曾经的版本,以后就再也无法查询曾经的那个版本。
因此,我们每次修改之前,都要把修改前的版本“保存一份”。
如何保存?
很显然,最无脑的方法是直接将整棵线段树复制成两份,然后在其中一份上进行修改,另一份则可以保留。
此时假设节点数 \(n\) 为 \(10^5\),那么每棵线段树就需要 \(2\times10^5-1\) 个节点(此处使用动态开点线段树)。再假设操作数也是 \(10^5\) 级别的,那么总的空间就是 \(2\times10^{10}\) 级别的,直接炸。
那么就需要考虑,哪些空间是浪费的?
三、树结构
1. 空间优化
简便起见,在保存上一个版本时,我们管被复制的节点叫做被“分裂”。(此处注意与“线段树分裂”算法并没有关系)
那么在暴力算法中,每个节点都分裂成了的两个同样节点。
此处只考虑单点修改,在修改一个点时,只有它本身及其所有祖先节点的值发生了改变。
所以我们只让这些被改动的节点分裂,其余不管。
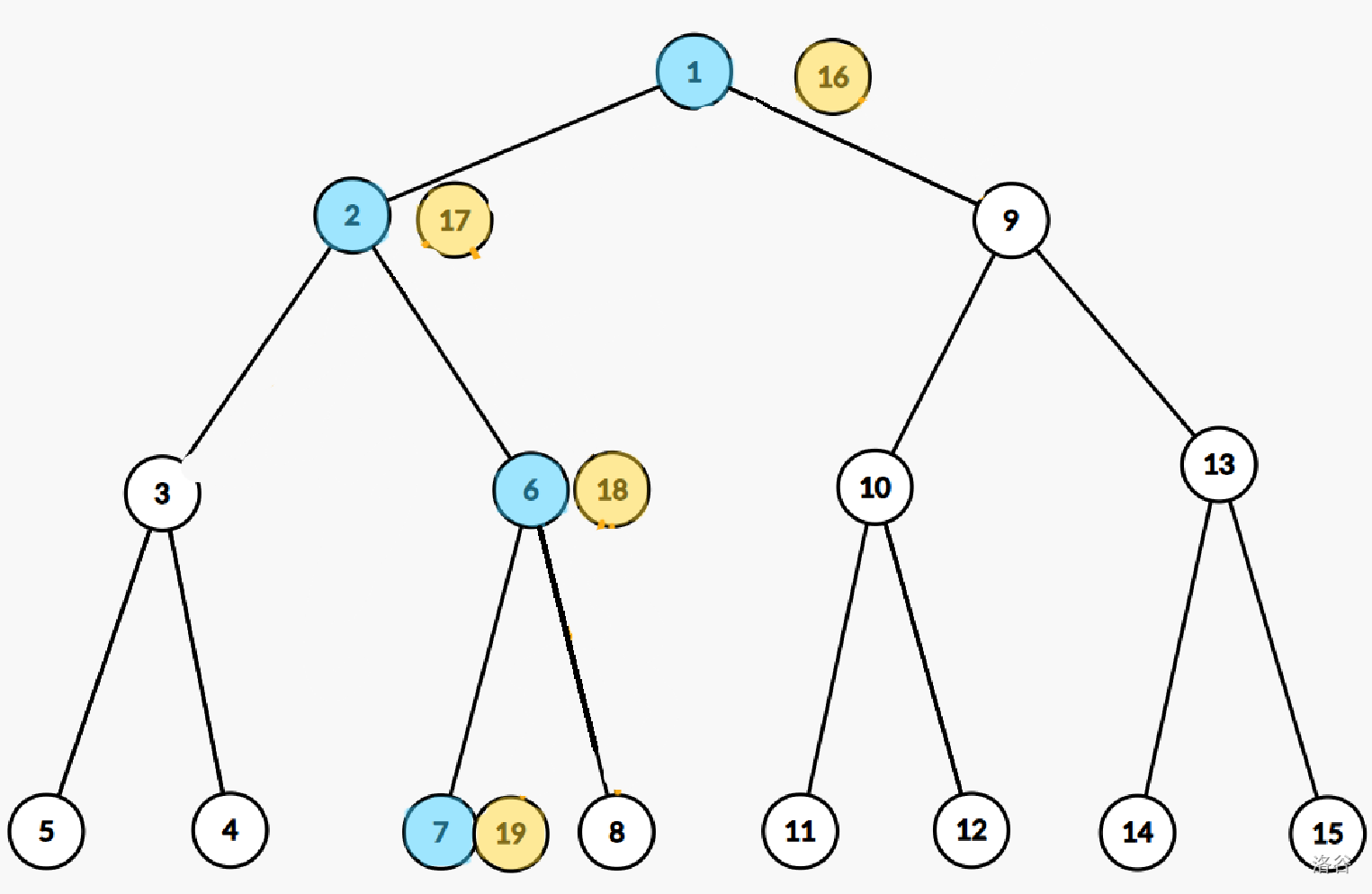
如图所示,假设我们要修改序列中的 \(3\) 号位,也就是图中树的 \(7\) 号节点,那么 \(1\),\(2\),\(6\),\(7\) 节点就会发生改变。
所以分裂它们,得到 \(16\),\(17\),\(18\),\(19\) 号节点,然后在这四个节点上进行修改即可。
按照原线段树的左右子树关系,这个线段树就长这个样子。
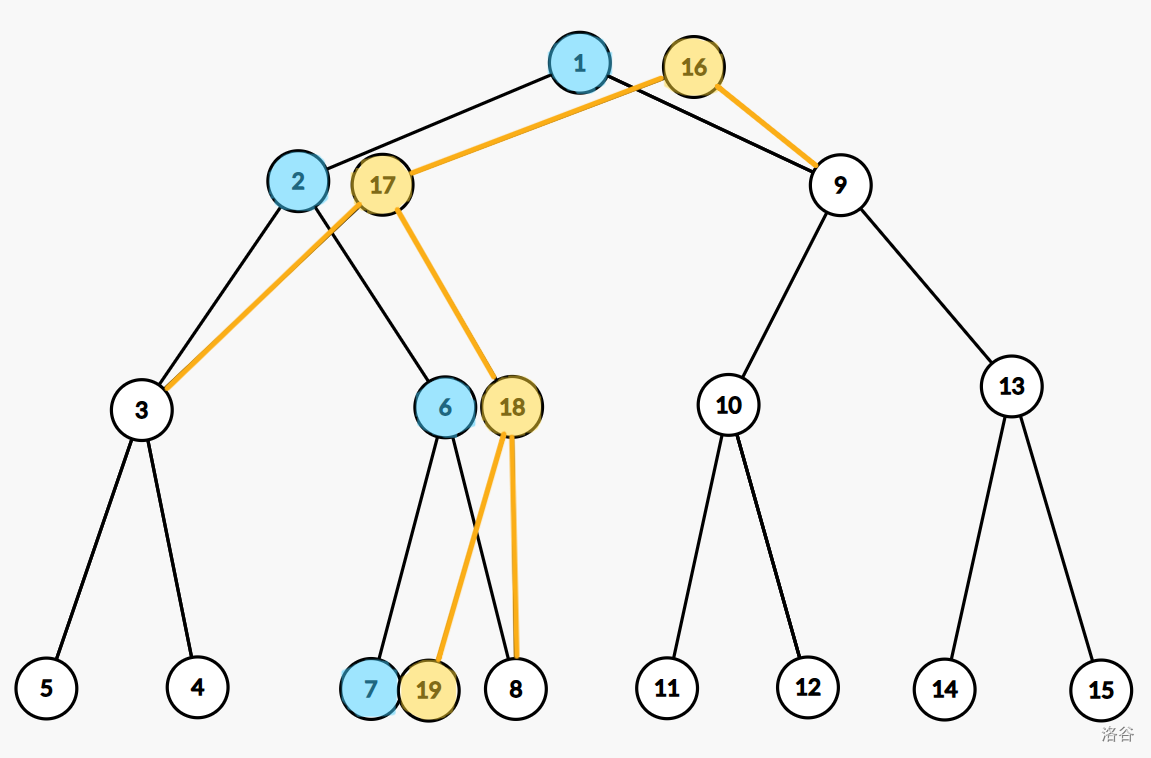
可以发现,图中其实包含了两个线段树,只不过他们共用了一些节点,所以空间就大大减少。
2. 修改节点
具体实现这个步骤也差不多:
- 建立先前版本根节点的副本。
- 先以先前版本根节点的左右儿子作为副本的左右儿子。
- 找要修改的节点在左子树还是在右子树。
- 如果在左子树,就递归,顺便把副本的左儿子改成先前版本根节点左儿子的副本。
- 在右子树同理。
- 剩下的那个儿子就还是原先的儿子,因为剩下的那一棵子树没有变化,与先前版本共用。
代码:
#define ls(p) st[p].l
#define rs(p) st[p].r
int update(int l,int r,int pos,int rt){
int create=++cnt;
ls(create)=ls(rt),rs(create)=rs(rt);
if(l==r){/*进行相应修改*/;return create;}
int mid=(l+r)>>1;
if(pos<=mid) ls(create)=update(l,mid,pos,ls(create));
else rs(create)=update(mid+1,r,pos,rs(create));
/*pushup*/
return create;
}
这个代码似乎有些难懂,下面还有一种写法:
#define ls(p) st[p].l
#define rs(p) st[p].r
void update(int l,int r,int pre,int &p){
p=++cnt;
ls(p)=ls(pre),rs(p)=rs(pre);
if(l==r) {/*进行相应修改*/;return ;}
int mid=(l+r)>>1;
if(pos<=mid) update(l,mid,ls(pre),ls(p));
else update(mid+1,r,rs(pre),rs(p));
/*pushup*/
}
注意这里 p 是引用类型(不知道怎么用?建议重学 C++),以及第一个写法中的 \(rt\) 或第二个写法的 \(pre\)。
最后主函数中我们定义 \(root_i\) 为第 \(i\) 个历史版本的线段树的根节点的编号。
显而易见,调用的时候应该调用 update(1,n,root[h],root[i]),意思是第 \(i\) 次操作时对编号为 \(h\) 的版本进行修改。
最好跟着代码手推一遍。
这个代码只是一个框架,具体的修改和 pushup 我并没有写。
其中 \(ls(p)\) 指节点 \(p\) 的左儿子,\(rs(p)\) 指节点 \(p\) 的右儿子,\(cnt\) 为总节点数。关于这个写法,我们下一节再说。
3. 树结构
不加优化的主席树就是整体分裂,而加优化的主席树就是局部分裂。而根据这种分裂方法,我们还能得出几个性质:
- 除叶子节点外,分裂之后的每个节点都有两个子节点。
- 每次修改后,根节点都会分裂。
- 每次修改会有 \(\log_2n\) 个节点分裂。
根据第一个和第二个性质,可以得到,给定某个根节点的版本,就可以确定一棵线段树。
再重申一遍,这棵线段树的某些节点可能与曾经的线段树共用,这代表这些节点在本次修改中没有被改变。
根据第三个性质,可以得到可持久化线段树的空间复杂度为 \(O(n+m\log n)\),\(m\) 为操作次数。
这样就绝对不会 MLE 了!
最后,再详细说一下新版本线段树的左右儿子关系。
当某个节点被复制,也就是分裂的时候,判断被修改的位置是在左子树还是右子树,我们管被修改的位置所处的子树叫做子树 \(A\),另一棵子树叫做子树 \(B\),那么这个分裂出来的新节点可以直接连向老版本线段树的子树 \(B\) 的根,这样子树 \(B\) 就共用了。然后把子树 \(A\) 的根分裂,连边之后向下走一步。
这一步还是挺简单的。
四、建树
与经典的线段树原理一样,只不过我们要使用动态开点线段树。
此时,节点 \(a\) 的左右儿子不再是 \(2a\) 和 \(2a+1\) ,而是 \(ls_a\) 和 \(rs_a\),分别表示 \(a\) 的左儿子和右儿子。
这样做的目的是,新版本的线段树因为有分裂操作,所以很难保证满足左右儿子为 \(2a\) 与 \(2a+1\) 的条件。
具体就是每次递归时新建一个节点,然后把这个新结点作为左儿子或右儿子,这可以用返回值的方法来实现。
int build(int l,int r){
int rt=++cnt;
if(l==r){
//此处进行基本的单点赋初始值
return rt;
}
int mid=(l+r)>>1;
ls(rt)=build(l,mid);
rs(rt)=build(mid+1,r);
//此处进行 pushup 操作
return rt;
}
可以发现,此时传参就不用传节点编号了。
还有就是,这种写法会省出一半空间,最原始的那棵线段树所使用的空间会从 \(4n\) 变为 \(2n\)。
五、常规操作
可持久化数据结构最经典的操作就是在某个历史版本中访问并修改。
我们以可持久化数组为例,要求:
- 修改某个历史版本中的一个值;
- 查询某个历史版本中的一个值。
对于第 \(i\) 个操作,生成一个新的版本,编号为 \(i\)。
初始数组的版本号为 \(0\)。
那么对于建树和修改来说应该是没有什么问题了,然后是query,与基本的线段树无异。
#include<bits/stdc++.h>
//#define int long long
using namespace std;
namespace Opshacom{
const int N=30000005;
int a[N],n,m,cnt,b[N];
class chairmantree{
public:
struct node{
int ls,rs,d;
}st[N];
void build(int l,int r,int &p){
p=++cnt;
if(l==r){
st[p].d=a[l];
return;
//return p;
}
int mid=(l+r)>>1;
build(l,mid,st[p].ls);
build(mid+1,r,st[p].rs);
//return p;
}
void update(int l,int r,int &p,int c,int x){
++cnt;
st[cnt]=st[p];
p=cnt;
if(l==r){
st[p].d=c;
return ;
// return p;
}
int mid=(l+r)>>1;
if(x<=mid) update(l,mid,st[p].ls,c,x);
if(x>mid) update(mid+1,r,st[p].rs,c,x);
}
int query(int l,int r,int p,int id){
if(l==r) return st[p].d;
int mid=(l+r)>>1;
if(id<=mid) return query(l,mid,st[p].ls,id);
else return query(mid+1,r,st[p].rs,id);
}
}cmt;
inline void work(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
cmt.build(1,n,b[0]);
for(int i=1;i<=m;i++){
int his,op,id,c;
cin>>his>>op;
if(op==1){
cin>>id>>c;
b[i]=b[his];
cmt.update(1,n,b[i],c,id);
}
else{
cin>>id;
cout<<cmt.query(1,n,b[his],id)<<"\n";
b[i]=b[his];
}
}
}
}
signed main(){
ios::sync_with_stdio(false);
Opshacom::work();
return 0;
}
码风比较清奇,主要是主函数中调用的部分是重点。
此题中需要注意的是 \(N\) 要开到 \(3e7\) 才能过。
六、区间 \(k\) 小值
到这里,我们再开始说真正的“主席树”,也就是可持久化权值线段树。
可持久化线段树 2 要求我们完成的操作是:
- 求出一个序列某个区间的第 \(k\) 小值。
其中 \(k\) 小值是指该区间从小到大排序后的第 \(k\) 个值。
1. 权值线段树
在学习这部分之前,最好先通过逆序对。
先考虑,如何求出序列的每个前缀的区间 \(k\) 小值。
用权值线段树维护一个 \(cnt\) 数组(其实是一个桶),初始的时候全为 \(0\)。
在计算长度为 \(i\) 的前缀的第 \(k\) 小值时,\(cnt_j\) 表示的是值 \(j\) 在 \(a_1\) 到 \(a_i\) 中出现的次数。
请仔细阅读上面这个定义。
这等价于,在算到前缀 \(i\) 的答案时,将 \(cnt_{a_i}\) 加 \(1\)。
然后,权值线段树要维护什么呢?
设 \(d_p=\displaystyle\sum_{i=l}^{r}cnt_i\)。区间 \([l,r]\) 为节点 \(p\) 的管辖区间。
每次查询时调用 query(1,mx,k,1)。
为了准确地表示出 query 的含义,我们举个例子。
假设目前的 \(i=8,k=5\),\(a\) 数组的前 \(8\) 项为:
那么此时的 \(cnt\) 即为:
建立线段树:

图中节点上的数字代表这个节点的 \(d\) 值。
初始的时候我们在根节点。
发现 \(k\) 小于等于左儿子的 \(d\) 值,所以答案一定在左子树内。(这一步应该很容易理解吧)
向下走一步,得到下图:
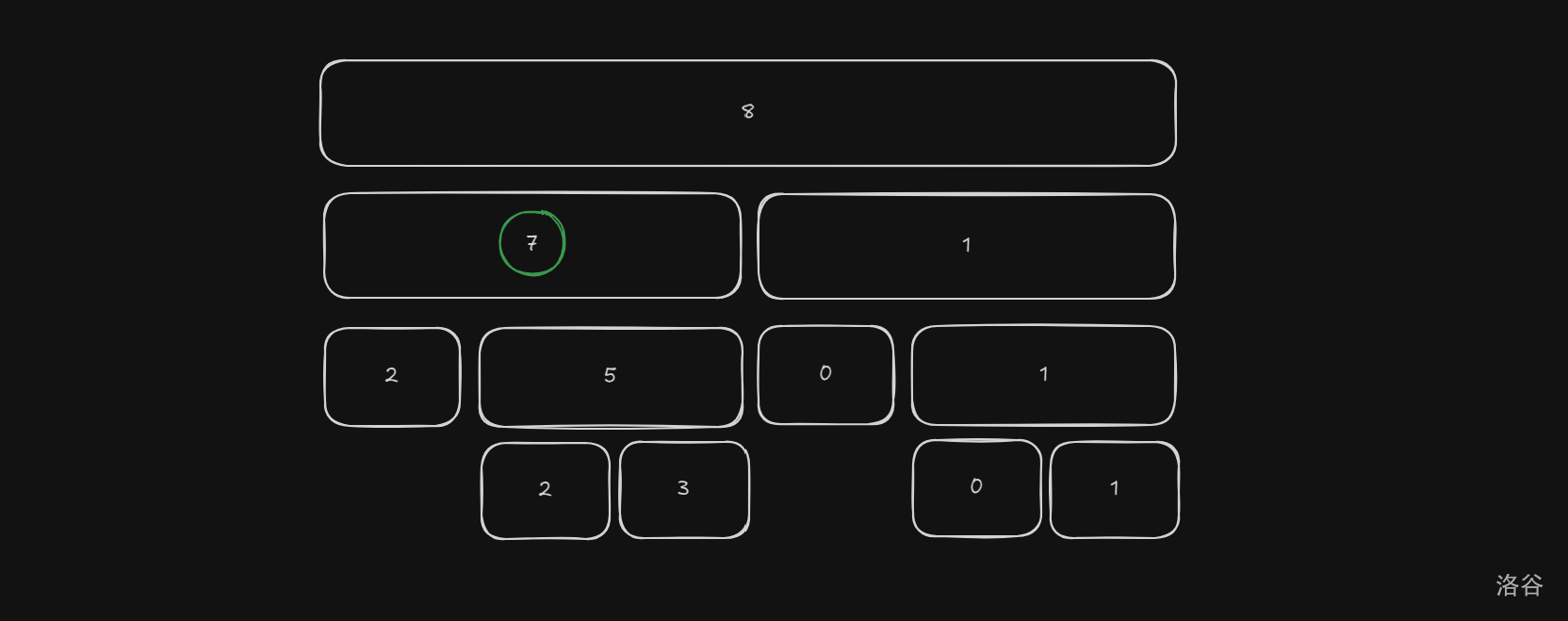
这次我们发现 \(k\) 大于左儿子的 \(d\),那就走到右子树。
重点!此时 \(k\) 需要减去左儿子的 \(d\),也就是说现在的 \(k\) 改为 \(3\)!
为什么呢?
现在就不得不提 query 的定义了。
query(l,r,k,p) 可以被定义为,可重集 \(S=\set{t\in\set{a_1,a_2,\cdots,a_i}|l\le t\le r}\) 的第 \(k\) 小值,\([l,r]\) 是 \(p\) 的管辖范围。
我非常喜欢数学语言,因为它比较严谨直观,且不容易发生歧义。
简便起见,我们记之为 \(Q(l,r,k)\)。
设 \(\mu=\lfloor\dfrac{l+r}{2}\rfloor\)。也就是代码中的 mid。
再设可重集 \(S_1=\set{t\in\set{a_1,a_2,\cdots,a_i}|l\le t\le \mu},S_2=\set{t\in\set{a_1, a_2,\cdots, a_i}|\mu+1\le t\le r}\)
如果 \(k\le|S_1|\),则 \(Q(l,r,k)=Q(l,\mu,k)\),否则 \(Q(l,r,k)=Q(\mu+1,r,k-|S_1|)\)。
这样就变得易于理解多了!因为 \(S_1\) 就是 \(S\) 中前 \(|S_1|\) 小的所有数,所以当 \(k>\mu\) 时,\(S_2\) 的第 \(k-|S_1|\) 小的值就是 \(S\) 中第 \(k\) 小的值啦!
综上所述,如果走右子树的话,\(k\) 需要减去左子树的 \(d\) 值。
于是向下走:
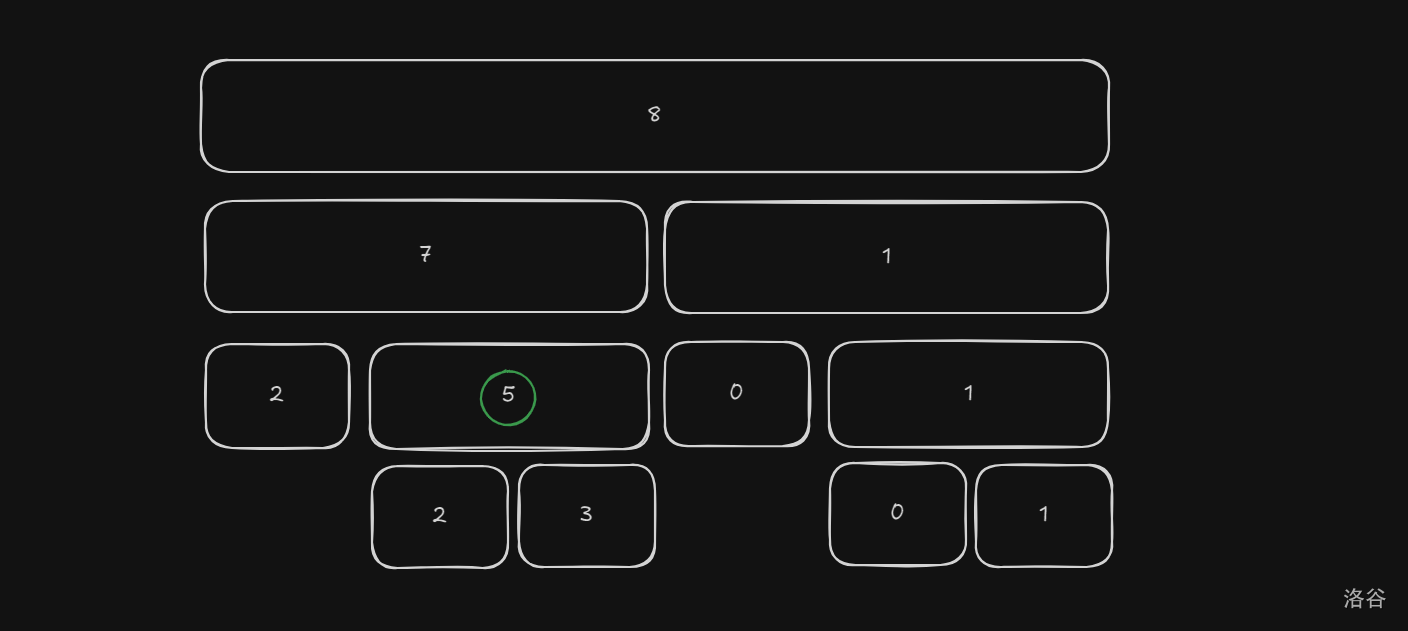
走完发现还在右子树(\(k>2\)), 于是 \(k\) 减去 \(2\),得到 \(1\)。

最后走到了值 \(3\) 所对应的叶子节点。
所以答案是 \(3\)。
一个例子跑完,对权值线段树的理解加深了不少。
代码:
int query(int l,int r,int k,int p){
int mid=(l+r)>>1,num=d[ls(p)];
if(l==r) return l;
if(k<=num) return query(l,mid,k,ls(p));
else return query(mid+1,r,k-num,rs(p));
}
2. 主席树
现在考虑任意区间的 \(k\) 小值。
还是以 \(\{3,1,2,3,3,6,1,2\}\) 为例。
当 \(i\) 为 \(3\) 的时候,\(cnt=\{1,1,1,0,0,0\}\)。
当 \(i\) 为 \(8\) 的时候,\(cnt=\{2,2,3,0,0,1\}\)。
也就是说,\(i\) 在从 \(4\) 到 \(8\) 的过程中,\(cnt\) 的变化量就是 \(\Delta cnt=\{+1,+1,+2,+0,+0,+1\}\)。
再回头一看,\(a_4\) 到 \(a_8\) 中,不就是恰好有 \(1\) 个 \(1\)、\(1\) 个 \(2\)、\(2\) 个 \(3\),和 \(1\) 个 \(6\) 吗?
所以就是说,通过 \(r\),\(l-1\) 两个版本的 \(cnt\) 的相减,就可以得到下标区间 \([l,r]\) 所对应的那个 \(\Delta cnt\),也就可以得到从 \(a_l\) 到 \(a_r\) 每个数字出现几次了!
这是非常好的。现在只需要考虑用可持久化权值线段树来记录 \(cnt\) 的每一个历史版本就好了!
具体地,对于每次 \(i\gets i+1\) 的时候,建立一个新的版本,然后在新的版本上对 \(cnt_{a_i}\) 进行加一就可以了。
数学地说,我们定义节点 \(\lambda,\rho\),为第 \(l-1\) 个版本以及第 \(r\) 个版本的线段树中,管辖范围为值域 \([L,R]\) 的两个节点。
再定义 \(cnt_i^{(h)}\) 为第 \(h\) 个版本中的 \(cnt_i\)。(\(h\) 阶导?)
与之前对 \(d\) 的定义几乎不变。
\(d_{\lambda}=\displaystyle\sum_{i=L}^R cnt_i^{(l-1)},d_{\rho}=\displaystyle\sum_{i=L}^R cnt_i^{(r)}\)。
那么设 \(\xi(l,r,L,R)=d_{\rho}-d_{\lambda}=\displaystyle\sum_{i=l}^r cnt_i^{(r)}-cnt_{i}^{(l-1)}\)。
和之前的方法一样,我们定义 \(Q(l,r,k,p)\) 为:可重集 \(\color{red}{S=\set{t\in\set{a_l,a_{l+1},\cdots,a_{r-1},a_r}|L\le t\le R}}\) 的第 \(k\) 小值,\([L,R]\) 是 \(p\) 的管辖范围。
这很合理。
设 \(\mu=\lfloor\dfrac{L+R}{2}\rfloor\)。也就是代码中的 mid。
再设可重集 \(S_1=\set{t\in\set{a_l,\cdots,a_r}|L\le t\le \mu},S_2=\set{t\in\set{a_l,\cdots, a_r}|\mu+1\le t\le R}\)
如果 \(k\le|S_1|\),则 \(Q(l,r,k,p)=Q(l,r,k,ls(p))\),否则 \(Q(l,r,k,p)=Q(l,r,k-|S_1|,rs(p))\)。
这样就比所谓“感性理解“看着好多了。
现在只需要算出 \(|S_1|\) 就可以了!
它不就是 \(\displaystyle\sum_{i=L}^\mu cnt_i^{(r)}-cnt_i^{(l-1)}\) 吗?不就是 \(\xi(l,r,L,\mu)\) 吗?
完美!
我们如复制粘贴般的就写好了 query :
int query(int l,int r,int s,int t,int k){
int mid=(s+t)>>1,xi=d[ls(r)]-d[ls(l)];
if(s==t) return s;
if(k<=xi) return query(ls(l),ls(r),s,mid,k);
else return query(rs(l),rs(r),mid+1,t,k-xi);
}
最后需要考虑的是求出 \(d\) 数组。
这简单多了,根据可持久化线段树的原理,在 query 之前先把先把整个序列遍历一遍,每遍历到一个数就执行之前说过的单点修改(也就是加 \(1\))即可。
void update(int l,int r,int pos,int rt,int &p){
p=++cnt;
ls(p)=ls(rt),rs(p)=rs(rt),d[p]=d[rt]+1;
if(l==r) return ;
int mid=(l+r)>>1;
if(pos<=mid) update(l,mid,pos,ls(rt),ls(p));
else update(mid+1,r,pos,rs(rt),rs(p));
}
值得一提的是,本题由于 \(a_i\) 的值是 \(10^9\) 级别,所以需要离散化。
(总不能对着一个 map 建线段树吧)
然后就通过了本题。
#include<bits/stdc++.h>
#define ls(p) st[p].ls
#define rs(p) st[p].rs
using namespace std;
namespace Opshacom{
const int N=5e6+7;
int n,m,a[N],tmp[N];
int len;
class Chairman{
private:struct node{int ls,rs;}st[N];
public:
int cnt,root[N],sum[N];
void build(int l,int r,int &p){
p=++cnt;
if(l==r) return ;
int mid=(l+r)>>1;
build(l,mid,ls(p));build(mid+1,r,rs(p));
}
void update(int l,int r,int pos,int rt,int &p){
p=++cnt;
ls(p)=ls(rt),rs(p)=rs(rt),sum[p]=sum[rt]+1;
if(l==r) return ;
int mid=(l+r)>>1;
if(pos<=mid) update(l,mid,pos,ls(rt),ls(p));
else update(mid+1,r,pos,rs(rt),rs(p));
}
int query(int l,int r,int s,int t,int k){
int mid=(s+t)>>1,num=sum[ls(r)]-sum[ls(l)];
if(s==t) return s;
if(k<=num) return query(ls(l),ls(r),s,mid,k);
else return query(rs(l),rs(r),mid+1,t,k-num);
}
}tr;
inline void Discretization(){
memcpy(tmp,a,sizeof(tmp));
sort(tmp+1,tmp+n+1);
len=unique(tmp+1,tmp+n+1)-tmp-1;
tr.build(1,len,tr.root[0]);
for(int i=1;i<=n;i++) tr.update(1,len,lower_bound(tmp+1,tmp+len+1,a[i])-tmp,tr.root[i-1],tr.root[i]);
}
inline void work(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
Discretization();
while(m--){
int l,r,k;
cin>>l>>r>>k;
cout<<tmp[tr.query(tr.root[l-1],tr.root[r],1,len,k)]<<"\n";
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
return Opshacom::work(),0;
}
代码其实挺短的,细节也不是很多?
其实这个还可以带修,套一个树状数组即可。因为『这是一篇(wǒ)面向(tài)普及选手(cài)的文章(le)』,所以不展开说。
七、树上第 \(k\) 小
例题:Count on a Tree。
其实就是求树上一条链上的第 \(k\) 小值。
乍一看是树链剖分,其实还是主席树的板。
在序列上,我们从前往后遍历,依次单点修改,每次生成一个新的历史版本。
在树上,我们按 DFS 的顺序遍历,依次单点修改,每次生成一个新的历史版本。
在序列上,\(\xi(l,r,L,R)=d_{\rho}-d_{\lambda}\),
在树上,\(\xi(l,r,L,R)=d_{\rho}+d_{\lambda}-d_{v}-d_{u}\)。
节点 \(\rho,\lambda,v,u\) 的管辖区间都是值域 \([L,R]\),它们所处的线段树的版本分别是 \(l,r,\operatorname{LCA}(l,r),fa(\operatorname{LCA}(l,r))\)。
其实就是树上差分的原理!
AC 代码:(竟然一遍过)
#include<bits/stdc++.h>
using namespace std;
int n,m;const int N=2e5+5;
struct edge{int to,nxt;}e[N<<1];
int head[N],cntt;
inline void add(int u,int v){
e[++cntt].to=v;
e[cntt].nxt=head[u];
head[u]=cntt;
}
int cnt,sum[N<<5],ls[N<<5],rs[N<<5],a[N],tmp[N],len,root[N],fa[N],zx[N][32],dep[N];
void build(int l,int r,int &p){
p=++cnt;
if(l==r) return ;
int mid=(l+r)>>1;
build(l,mid,ls[p]);
build(mid+1,r,rs[p]);
}
void update(int id,int l,int r,int lst,int &p){
p=++cnt;
ls[p]=ls[lst],rs[p]=rs[lst],sum[p]=sum[lst]+1;
if(l==r) return ;
int mid=(l+r)>>1;
if(id<=mid) update(id,l,mid,ls[lst],ls[p]);
else update(id,mid+1,r,rs[lst],rs[p]);
}
inline void Discretization(){
memcpy(tmp,a,sizeof(tmp));
sort(tmp+1,tmp+n+1);
len=unique(tmp+1,tmp+n+1)-tmp-1;
build(1,len,root[0]);
}
void dfs(int u){
update(lower_bound(tmp+1,tmp+len+1,a[u])-tmp,1,len,root[fa[u]],root[u]);
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa[u]) continue;
fa[v]=u;dep[v]=dep[u]+1;dfs(v);
}
}
int query(int l,int r,int lca,int flc,int s,int t,int k){
int num=sum[ls[l]]+sum[ls[r]]-sum[ls[lca]]-sum[ls[flc]];
if(s==t) return s;
int mid=(s+t)>>1;
if(k<=num) return query(ls[l],ls[r],ls[lca],ls[flc],s,mid,k);
else return query(rs[l],rs[r],rs[lca],rs[flc],mid+1,t,k-num);
}
inline void init(){
for(int i=1;i<=n;i++) zx[i][0]=fa[i];
for(int j=1;j<=30;j++) for(int i=1;i<=n;i++) zx[i][j]=zx[zx[i][j-1]][j-1];
}
int LCA(int u,int v){
if(u==v) return u;
if(dep[u]>dep[v]) swap(u,v);
for(int j=30;j>=0;j--) if(dep[u]<=dep[v]-(1<<j)) v=zx[v][j];
if(u==v) return u;
for(int j=30;j>=0;j--){if(zx[v][j]!=zx[u][j]){v=zx[v][j];u=zx[u][j];}}
return zx[u][0];
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
Discretization();
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
add(u,v);
add(v,u);
}
dep[1]=1;dfs(1);
init();
int lst=0;
while(m--){
int l,r,k;
cin>>l>>r>>k;
l^=lst;
int lca=LCA(l,r);int f=fa[lca];
lst=tmp[query(root[l],root[r],root[lca],root[f],1,len,k)];
cout<<lst<<"\n";
}
return 0;
}
完结撒花!





 浙公网安备 33010602011771号
浙公网安备 33010602011771号