Tet-Tetris 3D 线段树套线段树

题目链接：https://vjudge.net/problem/%E9%BB%91%E6%9A%97%E7%88%86%E7%82%B8-1513

题意：中文题目就自己看啦~

思路：题目本身不复杂，显然就是二维区间找最大值，然后二维区间修改，主要还是来学树套树的，所以下面就分享下自己理解的树套树。

有一个4*4的方格，把长度看成A，把宽度看成B，修改x轴【2,3】，y轴【2,4】的部分，就是修改图中红线的部分

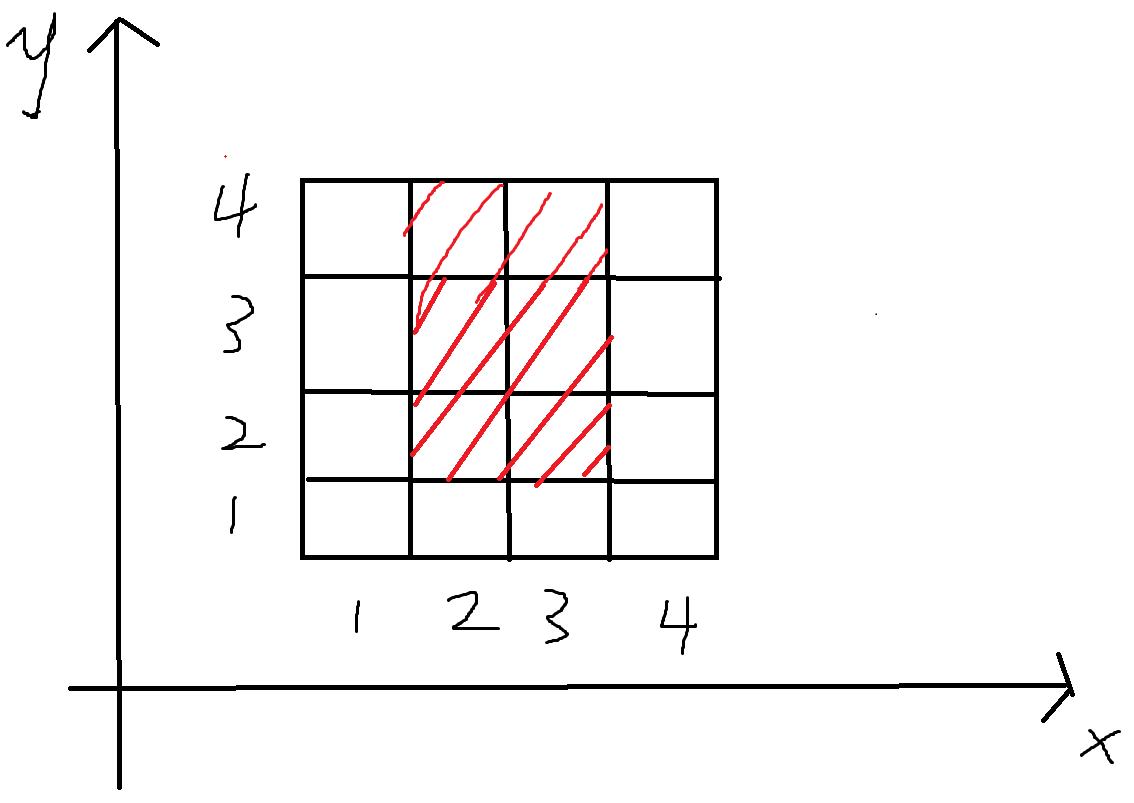
这里显然就有2个区间，一个是x轴的【2,3】，一个是y轴的【2,4】

那么我们就用一种线段树维护x轴的区间，另一种线段树维护y轴（其实是外层线段树和内层线段树，这里说成x轴线段树和y轴线段树，个人感觉看着图会形象一点。。。）

对于维护x轴的线段树，每个节点都是一颗y轴的线段树，怎么理解呢？我们先把视角放到线段树最底层的那些节点（红色框起来的）。

 

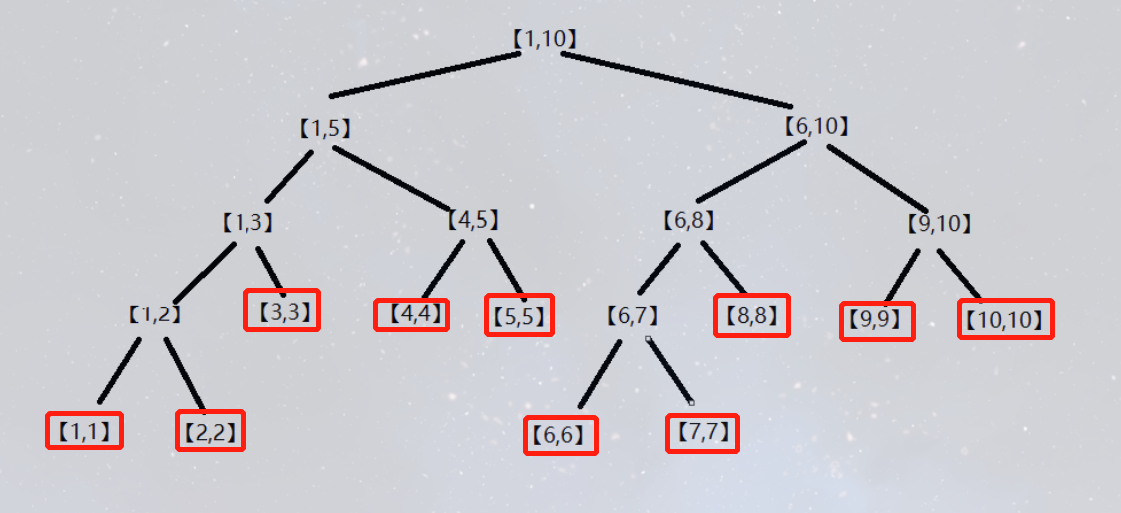
 这是一棵普通的线段树，最底下的节点都代表一个长度为1的区间，实际上就是区间上的某一个数。

但是对于树套树的外层树来说（就是维护x轴的树），这些长度为1的区间，都要看成一棵线段树。

举个例子，最下面的区间是【1,1】的节点，他是一棵维护 x = 1, y = 【1，B】的线段树，就是下图红色框柱的部分。（B是矩阵宽度，这里B = 4）

 

 

 

 

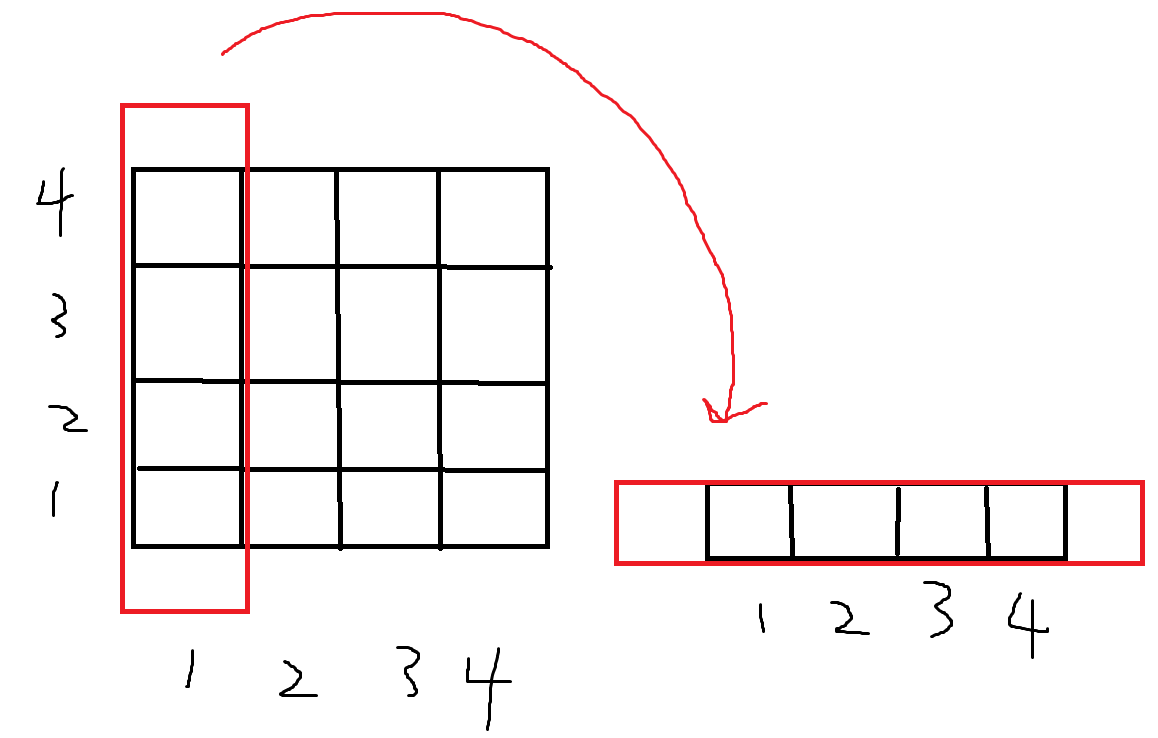
看了图就显而易见，红色框柱的其实是一段区间，他只有一个维度，把他横过来看，就和平时线段树处理的区间一样，完全可以用普通的线段树来维护。

所以对于x轴的线段树来说，他的每一个节点都是一棵线段树，每一颗线段树都是维护一个长度为B的区间

如果x轴的节点区间是【1,2】，那么他可以看成2个区间合成1个区间，然后再用一棵线段树维护，这个节点就是这棵线段树（如图，假设是维护区间和）

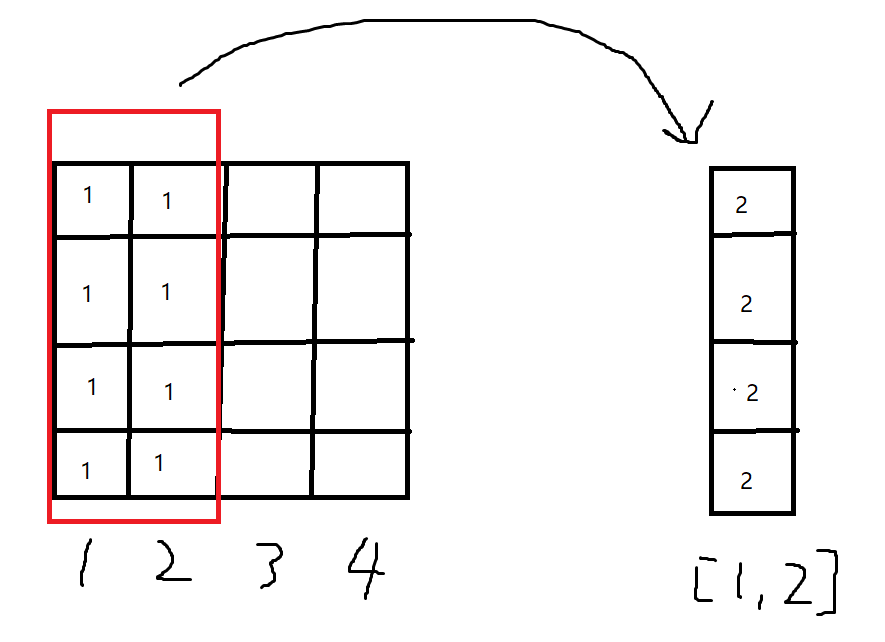
然后看看y轴的线段树，其实就是普通的线段树，相信看这篇博客的各位肯定都会了，就不说了~

个人感觉上，最难理解的是 “线段树的每个节点都是一棵线段树”，虽然说得很对但就是一脸懵逼QAQ....

---

 

理论讲完了，接下来聊聊具体实现

树套树是需要标记永久化的，因为对于x轴的线段树，每个节点相当于一棵线段树，他的一个pushdown/pushup就相当于在另一棵线段树上跑了一遍，时间爆炸，太容易被卡了。

标记永久化就相当于lazy数组（懒惰标记数组），不往下更新，处理到当前区间就改一下当前节点的lazy，查询答案的时候，如果要跑到这个区间下面，就必然会经过这个区间，也就可以更新到答案上。

本人线段树的lz是懒惰标记（标记永久化），tr是当前区间的最大值，注意一下更新的时候，每个节点都更新tr，但是懒惰标记是在return的那个节点那更新，每次查询的时候ans的初始值拿的是lz的值，因为

在当前区间不一定刚好是查的区间，会有别的区间，用tr作为ans初始值显然不合适，用lz作为初始值的话就相当于懒惰标记下传了。

实际操作的时候，假设修改x轴【l，r】，y轴【ll，rr】的部分，就先把这4个值更新，然后跑线段树，区间范围就容易写了，注意一下，两种线段树的长度和区间都不一定相同，写的时候留意一下。

代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1000 + 7;
int A,B,m,ll,rr;
struct treex {//内层 （y轴） 
    int tr[maxn<<2],lz[maxn<<2];
    void update(int l,int r,int rt,int L,int R,int c) {//[l,r]是节点区间，rt是节点编号，[L,R]是更新区间，c是更新的值，下同 
        tr[rt] = max(tr[rt],c);//当前区间必有[L,R]，直接更最大值 
        if(L<=l && r<=R) {
            lz[rt] = max(lz[rt],c);//标记永久化 
            return;
        }
        int mid = l + r >> 1;
        if(L<=mid) update(l,mid,rt<<1,L,R,c); 
        if(mid<R) update(mid+1,r,rt<<1|1,L,R,c);
    }
    int query(int l,int r,int rt,int L,int R) {
        if(L<=l && r<=R) {
            return tr[rt];
        }
        int mid = l + r >> 1;
        int ans = lz[rt];//拿出[l,r] 的标记作为初始化答案，下面的子区间都必有这个数 
        if(L<=mid) ans = max(ans,query(l,mid,rt<<1,L,R));
        if(mid<R) ans = max(ans,query(mid+1,r,rt<<1|1,L,R));
        return ans;
    }
};
struct treey {//外层 （x轴） 操作的是内层（y轴）线段树 
    treex tr[maxn<<2],lz[maxn<<2];
    void update(int l,int r,int rt,int L,int R,int c) {
        tr[rt].update(1,B,1,ll,rr,c);//更新的是y轴的线段树，注意一下区间长度和区间范围 ① 
        if(L<=l && r<=R) {
            lz[rt].update(1,B,1,ll,rr,c);//同 ①  
            return;
        }
        int mid = l + r >> 1;
        if(L<=mid) update(l,mid,rt<<1,L,R,c);
        if(mid<R) update(mid+1,r,rt<<1|1,L,R,c);
    }
    int query(int l,int r,int rt,int L,int R) {
        if(L<=l && r<=R) {
            return tr[rt].query(1,B,1,ll,rr);//同 ①  
        } 
        int mid = l + r >> 1;
        int ans = lz[rt].query(1,B,1,ll,rr);//同 ①  
        if(L<=mid) ans = max(ans,query(l,mid,rt<<1,L,R));
        if(mid<R) ans = max(ans,query(mid+1,r,rt<<1|1,L,R));
        return ans;
    }
}P;
int main()
{
    int d,s,w,x,y;
    int l,r;
    scanf("%d%d%d",&A,&B,&m);
    while(m--) {
        scanf("%d%d%d%d%d",&d,&s,&w,&x,&y);
        l = x + 1; r = x + d;
        ll = y + 1; rr = y + s;
        int mx = P.query(1,A,1,l,r);
        P.update(1,A,1,l,r,mx + w);
    }
    ll = 1; rr = B;
    printf("%d\n",P.query(1,A,1,1,A));
    return 0;
}